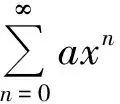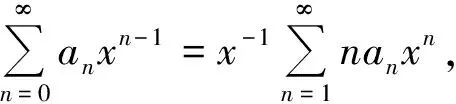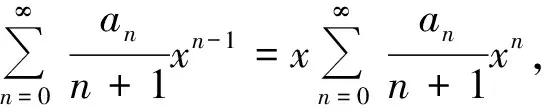基于上极限的幂级数收敛半径不变性质的证明
李典平
(恩施市施州民族小学,湖北 恩施 445000)
基于上极限的幂级数收敛半径不变性质的证明
李典平
(恩施市施州民族小学,湖北 恩施 445000)
运用上、下极限的理论,建立了数列上极限的2个引理。应用这2个引理,给出了幂级数逐项微分、逐项积分后收敛半径不变的性质定理的一个新证明,新证法较之原方法更为简明。
上极限;幂级数;收敛半径
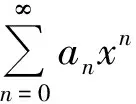
定理A(D′Alembent比值法) 若:
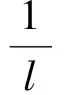
定理B(Canchy-Adamart公式) 若:
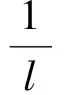
一般而言,定理A使用较方便,但定理B应用范围更广泛。
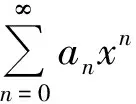
则有:
上述性质分别得到2个新的幂级数,它们的收敛半径不变,仍为R。在一般的《数学分析》[1]教材中,此性质定理都是运用Abel定理进行证明的。
下面,笔者建立了关于上极限的2个引理,并应用这2个引理给出了上述性质定理的一个新证明方法。
1 引 理
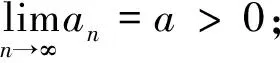
证明由定义,∀ε>0式不妨设ε
0 (1) bn (2) 且存在{bn}的子列{bnk},使得: 0 (3) 结合式(1~3)有: anbn<(a+ε)(b+ε)=ab+ε(a+b)+ε2 (a-ε)(b-ε)=ab-ε(a+b)+ε2 由上级限的性质,有: 引理2是定理B(Canchy-Adamart公式)的逆命题。 关于幂级数在收敛区间内逐项微分、逐项积分后以得新的幂级数收敛半径不变的性质重述如下。 证明仅须考虑R>0的情形,由引理2有: 又由引理1: 再由定理B,即得定理1结论为真。 [1]华东师范大学数学系.数学分析[M].第4版.北京:高等教育出版社,2010. [编辑] 洪云飞 10.3969/j.issn.1673-1409(N).2012.11.010 O171 2 A 16731409(2012)11N02802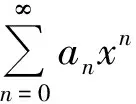
2 应 用