GDP、货币需求量和利率的VAR建模

邓 昕

(广州大学数学与信息科学学院，广东 广州 510405)

GDP、货币需求量和利率的VAR建模

邓 昕

(广州大学数学与信息科学学院，广东 广州 510405)

利用VAR模型，对中国GDP、货币需求量和利率进行建模、检验、分析和预测，并在此基础上提出相关货币政策的实施建议。

GDP；货币需求量；利率；VAR模型

GDP、货币需求量、利率是重要的经济指标和工具，也是国家制定货币政策的重要依据，对国家的经济发展至关重要。通过对三者的科学分析及合理调整可以实现对国家经济的有效控制。近年来 ，国内外学者对GDP、货币需求量、利率等重要经济指标进行了大量研究。他们应用VAR模型对货币政策的分析及其预测有着现实的借鉴意义[1]。据观察，无论国外还是国内，对于GDP、货币需求量、利率等重要经济指标在货币政策中的影响分析[2]，虽然有多种方式和形式，但大多数的研究要么停留在对单独经济指标或工具的研究上[3]，要么是通过研究其中的1～2个因素来预测分析经济形式[4]，这样是不够完善和全面的。笔者认为对中国经济发展状况的影响存在诸多因素，任何缺乏多元、系统、综合的思考都会使原有模型预测的准确性大大降低。为此，笔者基于理论基础上的实证研究，将规范分析与实证分析相结合，以时间序列和金融模型分析理论为指导，在归纳吸收国内外学者对GDP、货币需求量、利率等已有研究成果的基础上，实证分析2000年以来我国GDP、货币需求量、利率对经济的影响程度，并结合经济现状，提出针对性的政策建议。

1 VAR模型的建立

1)国内生产总值GDP 选用数据摘自《中国统计年鉴》(国家统计局年度数据 ISO版)2000年第1季度至2011年第4季度的按属性分季度的国内生产总值(GDP)指标。

2)货币需求量 选用数据摘自《中国统计年鉴》、《中国金融年鉴》(国家统计局 ISO版)2000年第1季度至2011年第4季度的实际货币需求量指标。

3)利率 采用具有代表性的一年期定期存款利率，首先考虑我国利率在样本数据所在区间的多次调整，假如某些年度对存款利率进行了调整，则以实际执行时间为权数进行加权平均而得到的数值为准。然后要考虑当期通货膨胀率，同时为了让整个样本区间内的实际利率具有可比性，以此生成新的数据样本，并对所有数据进行标准化和对数处理。笔者研究中数据的时间段为2000年第1季度到2011年第4季度，在此期间国家经历了通货膨胀和通货紧缩，政府分别采用了扩张性、紧缩性和稳健的货币政策。

笔者对样本数据的实际利率采用正态分布的分布函数作标准化处理，标准化到0～1。即用样本的均值与方差作为总体的期望和方差，然后对每个值求它对应的分布概率，对原始数据-实际利率进行线性变换。得出标准化数据后均等放大100000倍，以便于在VAR模型中差分分析时进行数据应用和对数处理。

2 模型的检验和预测

表1 时间序列模型的数据

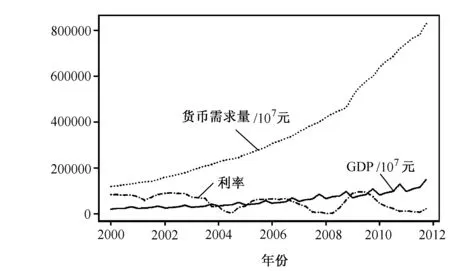
图1 中国GDP、货币需求量和实际利率季度数据的时间序列

1)ACF检验 由于虚假回归问题的存在，所以进行动态回归模型拟合时，必须先检验各序列的平稳性。笔者采用ACF检验法对GDP、货币需求量和利率3个序列的平稳性进行检验。在S-Plus时间序列分析软件中首先输入数据，其次逐步进行检验，即先对中国GDP、货币需求量和利率数据进行初步指标分析，明确样本均值和方差、最大值和最小值、中位数、方差和残差等，如表1所示。分析数据的相关性，其结果如表2所示。由表2可知，GDP和货币需求量之间的线性相关程度很高，而GDP和货币需求量均与利率成负相关。然后应用S-Plus时间序列分析软件画出中国GDP、货币需求量和利率数据的时间序列图(见图1)和ACF(见图2)。对于GDP和货币需求量，可观察出它们的变化趋势相关性很高：不仅是自变化的趋势，还有随实际利率变动的趋势。对于利率，可看出其存在一个比较清晰的季节模式，且在季节周期内实际利率的变化相对比较平稳。

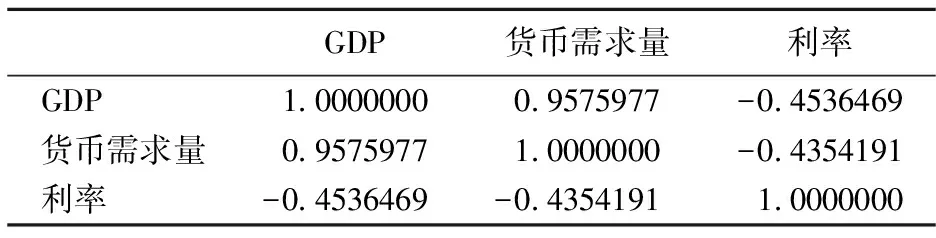
表2 数据的相关系数

2)数据的差分处理 由表1、表2、图1可以看出，原始数据有一个趋势，因此可以认为中国GDP、货币需求量和实际利率的季度数据是非平稳的。通过取对数后再一阶差分可得到数据的对数一阶差分序列图(见图2)，并对中国GDP、货币需求量和实际利率的差分数据的样本做ACF分析。

笔者选择用AR函数来拟合VAR模型，并选择用AIC准则来选择阶数。应用S-Plus时间序列分析软件求得阶数为4，从而得到参数估计和残差图(见图3)：

表3 线性回归方程

图2 中国GDP、货币需求量和实际利率季度数据的对数一阶差分序列图

图3 中国GDP、货币需求量和实际利率季度数据的残差时间序列图

3)回归诊断 回归诊断前，应先对数据模拟拟合。模型的拟合采用经典的最小二乘法来实现，结果如表3所示(事实上，在正态分布假设条件下，最小二乘估计与最大似然估计是等价的)。其中，复相关系数说明回归方程可以解释大于多少百分比的Y值的变化，如GDP与货币需求量的线性回归方程可以解释为大约91.7%的与货币需求量相关的GDP变化。F-统计量(P值)表明了对回归方程的整体检验，若其检验的P值为0，表示回归方程是非常显著的，相较之下实际利率和GDP、货币需求量的回归方程则不显著。对含3个变量的关于中国GDP、货币需求量和实际利率季度数据的多元线性回归模型进行回归诊断，结果如图4所示。

根据图4(a)、(b)可知，残差对拟合值散点和残差绝对值平方根对拟合值散点中均没有异常值和异方差存在，残差中也没有趋势成分，故可认为数据都是平稳的；图4(c)是用来判断模型的拟合优度，因变量对拟合值的散点与回归线越接近，拟合程度越好；图4(d)为残差的正态QQ图，其中点基本与QQ线重合，因此可认为残差服从正态分布，因而模型的正态分布假设正确；图4(e)为残差和拟合值的取值范围图，通过对比拟合值的取值范围和残差的取值范围解释观测值的变动，可看出拟合值的范围小于残差的范围，则变量对因变量的作用是不显著的；图4(f)为Cook距离图，图中标明的重大影响点36,39,48分别与时事对应，反映其时中国经济的实际状况：即36点代表2008年第3季度(2008年9月9日，全球金融危机开始失控，并导致多所相当大型的金融机构倒闭或被政府接管，自然对中国的GDP、货币需求量和利率等经济造成较大影响)；39点代表2009年第2季度(时逢国内新医改方案推行、人民币跨境贸易结算试点运行等一系列经济政策的实行)；48点代表2011年第3季度(继美国主权债务评级遭降之后环球股市溃不成军，又有欧洲债务危机频频烦扰，致使国内经济压力徒增，中国政府开始适度放松货币政策，对市场提供流动性支撑经济)。

3 预 测

表4 2012年后10个季度的中国GDP、货币需求量和实际利率的预测结果

依据从2000～2011年的中国GDP、货币需求量和实际利率季度数据拟合出的模型，利用S-Plus时间序列分析软件预测2012年后10个季度的中国GDP、货币需求量和实际利率的有关数据(见表4)。与当前中国经济现状相较，2012年中国前3个季度流通中货币分别为59820.72、51448.78、49595.75亿元人民币(数据来自中国人民银行2012年统计数据)，且是“实际负利率”。由此可以看出，表4中预测值的总体趋势与观察序列的趋势大致相符。

需要说明的是，在模型的建立过程中，笔者仅仅只是利用了中国GDP、货币需求量和实际利率季度数据自身的动态变化，并没有考虑其他外在因素的影响。而实际上，在一个指定的地区，对经济产生影响的因素不只是GDP、货币需求量和实际利率，诸如CPI(消费物价指数)、政府政策的调整等因素也会对宏观经济造成影响。虽然还需要深入研究，但通过运用该模型，已可以很好的预测其发展方向，这对推进制定宏观经济货币政策无疑具有很大的借鉴和帮助。

图4 中国GDP、货币需求量和实际利率季度数据的线性回归诊断图

[1]Christorpher A S.Macroeconomics and Reality[J].Econometrica,1980，48(1)：1-48.

[2]汤戈于，温峥. 我国货币数据与名义GDP的相关性研究及在货币政策中的运用[J].海南金融，2005(11)：16-20.

[3]单勤琴.基于VAR模型的货币政策传导机制的计量分析[D].长沙：湖南大学,2006.

[4]徐丹丹,孟潇.我国适度宽松货币政策走向——基于货币政策对货币供给量、GDP以及物价水平影响判断[J].经济理论和经济管理，2010(4)：25-28.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.11.008

O29；F832 2

A

16731409(2012)11N02104