基于期望最大算法的高斯混合模型参数估计

余瑞艳

(长江大学一年级教学工作部，湖北 荆州 434023)

基于期望最大算法的高斯混合模型参数估计

余瑞艳

(长江大学一年级教学工作部，湖北 荆州 434023)

高斯混合模型(GMM)已在图像处理和计算机视觉领域得到了广泛应用，对于该GMM模型中各项参数的估计依然是一件值得研究的问题。采用期望最大算法(EM)来估计该模型对应的多参数，并给出其详细的推导过程。试验结果表明，EM算法在估计GMM模型中各项参数时具有很强的鲁棒性，并取得了很好的效果。

期望最大算法；高斯混合模型；估计

在图像处理(image processing)和计算机视觉(computer vision)领域，常利用自然图像的统计模型将对应的问题转化为图像的Bayes估计问题，正确的图像统计模型可作为先验知识或约束项来增强该问题估计过程中的鲁棒性。近年来，拉普拉斯先验(Laplacian Prior)模型与超拉普拉斯先验(Hyper-Laplacian Prior)模型已被广泛应用于自然图像梯度分布的统计分析[1-3]，并取得了很好的应用效果。2006年，Fergus采用高斯混合模型(Gaussian Mixture Model, GMM)来拟合自然图像的先验分布，有效地解决了运动模糊图像的盲复原问题[4]。进一步地，GMM模型在理论与实际应用上得到了广泛的应用[5-10]。虽然GMM模型在众多工程领域得到了广泛的研究，且基于GMM模型的数学方法取得了很好的应用。但GMM模型中需估计的多参数限制了该模型在实际问题中的应用，因此对于GMM模型中的多参数估计是值得研究的问题。下面，笔者将采用期望最大算法(Expectation Maximization Algorithm, EM)来估计对应GMM模型中的多参数，并利用实际案例来检验EM算法在GMM模型中的有效性。

1 高斯混合模型

高斯混合模型(GMM)是由C个单一的高斯模型N(x|μ,ϑ)构建而成，参数C依实际情况而定：

(1)

假设不完全数据(incomplete data)x中的每个概率密度函数分量pc(x|μc,ϑc)服从d维高斯分布：

(2)

2 GMM参数估计中的EM算法

式(1)中不完全数据x的对数似然函数(log-likelihood expression)[11]为：

(3)

式中，“子集核”θc⊂Θ。对含log的式(3)难以优化求解，为此引入一组指示函数y={y1,y2,…,yN}：{yi=k|xi属于第k个单一高斯模型},且满足yi∈{1,2,…,C}。此时对数似然函数(3)可转化成：

(4)

的优化求解。由Bayes公式，有:

根据基本EM算法中的“E-步骤”[11]，式(4)又可转化成如下问题的求解:

(5)

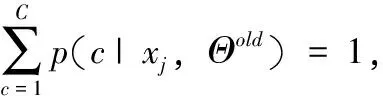
根据概率密度函数分量pc(x|μc,ϑc)的定义，对其两边取自然对数，忽略其中的常数项，并与式(6)联立起来，有：

(7)

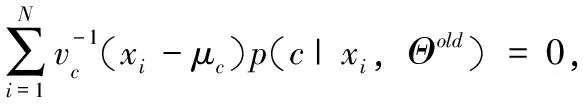
在有效估计期望μc的基础上，接下来估计方差ϑc，此时式(7)可重新改写成：

(8)

式中，矩阵的迹tr(·)表示成对应矩阵的特征值之和，且Nc,i=(xi-μc)(xi-μc)T。

综上所述，估计高斯混合模型(GMM)中各项参数的EM算法为：

图1 概率统计直方图与GMM拟合曲线

3 试验结果及分析

例1假设一高斯混合模型的函数表达式为：

GMM=0.3Ν(1,1)+0.7N(1,9)

(9)

其对应的概率统计直方图如图1所示。

利用笔者介绍的EM算法，得到GMM模型(9)中各参数的估计值，如表1所示。由表1中数据可以发现，利用笔者介绍的EM算法可以很好地估计了GMM模型中的各项参数，其对应的拟合曲线较好地逼近了真实的概率分布情形(见图1)。

4 结 语

表1 GMM模型中的各参数的估计值

高斯混合模型(GMM)已被广泛地应用地图像处理领域，并取得了令人满意的效果。但对于GMM模型中对应参数的估计，依然是一个值得继续探讨的问题。笔者给出了估计GMM模型中各项参数(权重、期望与方差)的期望最大算法EM，推导了其详细的计算过程。并基于1个实际案例，验证了EM算法在估计GMM模型中各项参数的有效性和鲁棒性，为GMM模型在图像处理中的进一步应用奠定了基础。

[1]Levin A.Blind motion deblurring using image statistics[C]//Proceedings of Advances in Neural Information Processing Systems, 2006, 19: 841-848.

[2]Levin A, Fergus R，Freeman W T.Image and depth from a conventional camera with a coded aperture[J] .ACM Transactions on Graphics, 2007, 26(6): 70-77.

[3]刘文, 吴传生, 吕琪.含噪径向模糊图像的复原算法研究[J].武汉理工大学学报, 2011, 33(4): 139-143.

[4]Fergus R, Singh B, Hertzmann A, et al.Removing camera shake from a single photograph[J] .ACM Transactions on Graphics, 2006, 25(3): 787-794.

[5]刘文.空间变化运动模糊图像的复原算法研究[D].武汉: 武汉理工大学, 2011.

[6]李明, 赵勋杰.改进的基于高斯混合模型的运动目标检测算法[J].计算机工程与应用, 2011, 47(8): 204-206.

[7]何信华, 赵龙.基于改进高斯混合模型的实时运动目标检测与跟踪[J].计算机应用研究, 2010, 27(12): 4768-4771.

[8]Hammond D K, Simoncelli E P.Image denoising with an orientation-adaptive Gaussian scale mixture model[C]//Proceedings of IEEE International Conference on Image Processing, Atlanta: IEEE Computer Society, 2006:1433-1436.

[9]Permuter H, Francos J，Jermyn I.A study of Gaussian mixture models of color and texture features for image classification and segmentation[J].Pattern Recognition, 2006, 39(4): 695-706.

[10]熊彪, 江万涛, 李乐林.基于高斯混合模型的遥感影像半监督分类[J].武汉大学学报(信息科学版), 2011, 36(1): 108-112.

[11]Mitchell T M.Machine learning[M].New York: The McGraw-Hill Company, 2002.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.11.005

TP301 6

A

16731409(2012)11N01203