城市水资源质量系统动力学仿真与评价研究
毛敏华
(南水北调中线干线建设管理局机电物资部,北京 100382)
城市水资源质量系统动力学仿真与评价研究
毛敏华
(南水北调中线干线建设管理局机电物资部,北京 100382)
在分析城市水资源质量影响因素的基础上,建立了城市水资源质量系统动力学仿真模型,模型由工业用水子系统、城市居民用水子系统及水污染处理子系统构成。通过W市实际统计数据对模型调试检验后,以工业产值增长率、人口增长率和污水处理率为决策变量,以3种发展方案对W市未来20年的COD排放量仿真,仿真结果说明城市发展规划需要协调发展,特别是对人口增长率及水污染处理率不能忽视。
水资源质量;系统动力学;仿真;评价
水是城市经济协调健康发展的战略性基础资源,也是生态环境系统维持良性循环的控制性要素,城市经济发展和水安全之间的互动影响关系越来越受到重视[1]。城市飞速发展的同时给区域内用水安全带来了更大的压力,保证城市水资源质量已是一个很重要的课题。
在对城市水资源质量的研究中,大部分主要针对居民生活废水的净化再利用环节进行研究,李梅将系统动力学应用于污水再生利用的系统分析和预测[2];徐志嫱等用系统动力学方法建立了分散式污水再生回用系统模型[3];黄微等在污水再生利用规划中运用系统动力学模型针对石家庄特点设计多情景,并以非线性优化方法得到具体再生水水源和回用对象的配水方案[4]。以上的研究中将城市居民生活用水造成的污染作为城市水资源质量单一影响因素进行分析,但实际情况中工业的发展也是城市的重要组成部分;与此同时,在水资源承载力、需水量预测、水资源供需平衡分析等方面也开展了广泛的研究,但存在系统结构不完整、反馈回路断裂的问题影响系统模拟效果,且未对水体质量作深入分析。
系统动力学(system dynamics, SD)是一种将结构、功能和历史相结合,以反馈控制理论为基础,借助计算机进行模拟仿真而定量地研究高阶次、非线性、多重反馈复杂时变系统的系统分析理论和方法,是研究具有复杂反馈关系系统的重要方法。其本质是带时滞的一阶微分方程组,可作为实际系统,特别是社会、经济、生态等复杂大系统的“实验室”,是研究水资源系统的重要方法之一[5]。
下面,笔者针对城市水资源质量变化影响因素,应用系统动力学方法对其进行仿真建模分析,通过已有的经济水文数据检验调试模型的精度后,选取工业产值增长率、人口增长率和污水处理率为决策变量,通过3种不同的城市发展方案对W市未来20年水资源质量进程仿真,通过仿真结果的分析对城市未来发展规划提出相应的政策建议。
1 城市水资源质量SD模型的建立
城市水资源的主要污染源为居民生活污水及工业污水,经过污水处理设施后,这部分水再次进入城市内部循环,建立系统动力学模型首先需要对建模的目的及模型边界、假设条件等进行确定。笔者建立的城市水资源质量模型,拟解决以下几个问题:①更加直观的表现城市水资源质量的主要影响因素,特别是经济发展导致居民生活用水及工业用水的增加,同时经济的发展也会使城市水污染处理能力的增加,通过建模较为直观的表述上述因素之前的相互作用、相互影响的关系;②通过调节模型决策变量来制定多种方案,模拟不同方案下水资源质量的变化情况;③定量描述W市未来20年水资源质量的动态变化情况;④将各方案对比分析,确定最优方案,为决策者提供依据。
由于数学模型是现实情况的抽象变现,故允许存在一定的误差,笔者建立的城市水资源质量系统动力学模型的边界为对象城市范围内,将城市的水资源相对独立起来进行研究,且假设城市污水处理能力不足。
建模的主要目的及模型的边界、相关假设条件确定后,运用系统动力学软件Vensim PLE得到城市水资源质量主要因果关系回路,按照城市主要污水产生系统分为居民生活污水及工业产生污水,具体的城市水资源质量主要因果关系回路如图1所示。图1中共有2个正(+)反馈回路:工业产值、城市人口-社会总产值-污水处理投资-污水处理量-COD排放量-水资源质量-工业产值、城市人口,在一定时期内,随着工业产值及城市人口的增加,社会总产值必将随之增加,于是政府对污水治理投资加大,COD排放下降,从而使水资源质量上升,反过来进一步促进工业产值及城市人口的增加;2个负(-)反馈回路:工业产值、城市人口-总污水量-直接排放量-COD排放量-水资源质量,主要表现为工业产值和城市人口使得总体污水排放量增加,尽管污水处理能力也在上升,但总体结果还是导致COD排放量上升,并最终导致水质恶化[6]。
2 城市水资源质量SD分析

图1 城市水资源质量主要因果关系回路
城市水资源质量主要因果关系回路如图1所示,由图1可知城市水资源污染源主要分为工业污染和居民生活污染,同时将水污染处理作为单独的子系统,将工业用水、城市居民用水和水污染处理分别作为独立的子系统作详细的系统动力学分析[7]。
2.1 工业用水子系统
工业用水子系统即城市中工业导致的污水量及相应的污水处理系统。该方法是通过调查工业万元产值取水量的现状和历史变化趋势,推测目前或将来为实现某一工业产值目标所需的工业用水量,并通过单位产值工业污水产生率研究相应时间段内工业污水的产生量。该子系统的核心变量是工业产值,由于工业用水的统计数据相对较少,该研究通过设定表函数,结合城市相关发展规划指标的方法来表示工业产值增长率,确定工业用水量的变化状况。该系统SD结构如图2所示。
2.2 城市居民用水子系统
选定人口数量作为流位变量,人口变化率作为流率变量,总人口变化率可以通过多年的统计数据,通过VENSIM 软件的表函数、分段函数相结合的方法来确定。该系统SD结构图如图3所示。

图2 工业用水子系统 图3 城市居民用水子系统
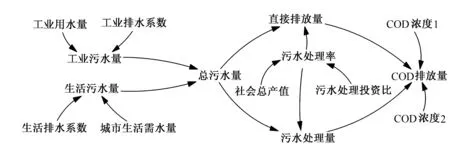
图4 水污染处理子系统
2.3 水污染处理子系统
工业用水子系统及城市居民生活用水子系统产生的污水通过城市污水处理系统处理后排放(见图4),由于城市内污水处理能力有限,故有一部分废水直接排放,处理后污水与直接排放污水的区别在于COD浓度的不同,同时随着工业产值与城市人口的增加,导致社会总产值的上升,政府加大污水处理力度使得污水处理率呈动态变化趋势。
3 模型的调试与检验
根据建模的目的,模型运行之前应对模型结构和功能进行全面的检验,以保障模型的有效性和真实性。系统动力学模型的适用性与一致性的检验过程包括以下4组:结构的合适性检验、模型行为的适用性检验、模型结构与实际系统的一致性检验、模型行为与实际系统的一致性检验[8]。

表1 模型的运行结果检验
将W市2006~2010 年的历史参数输入模型进行模型仿真,然后与历史实际发生的行为、数据进行对比。选取人口数量和工业产值进行历史验证。验证结果如表1所示。由表1可知,人口数量和工业产值的仿真结果与历史值基本符合,其中人口数量的最大误差不超过6%,工业产值额最大误差不超过2%,认为模型模拟结果与实际值拟合较好,可运用该模型进行仿真。
4 城市水资源SD仿真与结果分析
已建立的城市水资源质量SD模型通过实际数据的仿真检验保证了模型的精度符合要求,系统动力学又称为政策实验室,决策变量的选取引用多指标综合评价法中指标的选取原则,结合W市水资源质量影响因素的具体情况,选取工业产值增长率、人口增长率、污水处理率3个量作为决策变量。通过改变决策变量的值得到不同方案下相关指标的模拟结果。再通过对不同方案的模拟结果分析方案可取之处及需要改进的地方。
选取3个方案进行仿真模拟,其中方案1为现实情况,方案2及方案3为假设情况,具体3种情况的决策变量值如表2所示。这3种方案变现出了3种不同的城市发展理念,方案2主要强调保持工业产值的高速增长,同时对人口增长率的控制较方案1更为严格;方案3强调工业产值与人口增长率的稳步发展,虽然工业产值不如其他方案增加的快,但对人口增长控制最为严格,同时方案3对污水处理的投入更大,使污水处理率维持在一个高水平。通过SD模型仿真后,得出城市资源水质量动态变化情况,即COD排放量仿真结果如表3所示。
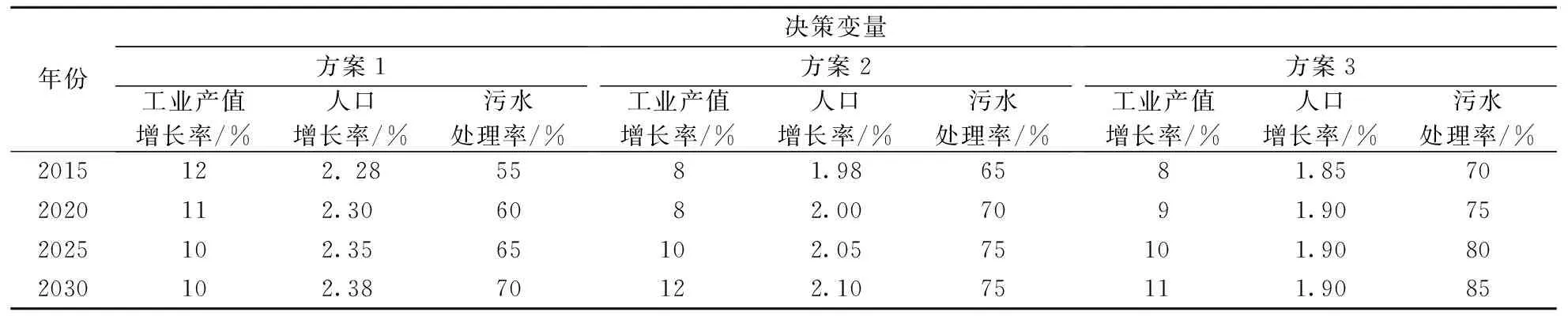
表2 各方案决策变量取值
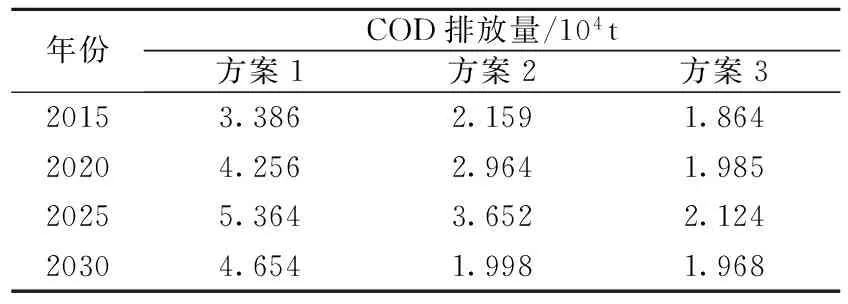
表3 各方案模拟仿真结果
以上仿真结果表明,针对W市水资源质量情况,工业用水量与城市居民用水量产生的污水是影响水质的主要原因,仿真方案中,虽然方案2的工业增长值最大,但由于对人口增长控制不严及污水处理率不高,COD排放量均大于方案3,同时该方案中还有很多指标有待改进,说明在城市的发展规划中,不能只关注工业产值的增长,人口的控制及污水处理水平的提升也不容忽视。
5 结 语
以城市水资源质量为研究对象,用系统动力学方法建模。通过W市实际统计数据对模型调试与检验后仿真,将模型仿真精度校准到规定范围后,选取城市发展规划中工业产值增长率、人口增长率及水污染治理率为决策变量,了解3个参数对COD排放量产生的影响,为城市发展相关政策分析起参考作用。仿真结果表明,只有工业产值增长率、人口增长率和水污染治理率协调发展才能保障城市水资源质量。
[1]钱正英, 张光斗. 中国可持续发展水资源战略研究综合报告及各专题报告[M].北京: 中国水利水电出版社, 2001.
[2] 李梅. 城市污水再生回用系统分析及模拟预测[D]. 西安:西安建筑科技大学, 2003.
[3] 徐志嫱, 黄廷林. 分散式污水再生回用系统优化分析[J]. 西安建筑科技大学学报, 2005,37(2): 164-168.
[4] 黄徽, 杜鹏飞,曾思育. 基于系统动力学模型的石家庄污水再生利用规划[J]. 清华大学学报(自然科学版),2010,50(3): 391-395.
[5] 王其藩. 系统动力学[M]. 上海:上海财经大学出版有限公司,2009.
[6] 王薇, 雷学东, 余新晓,等. 基于SD模型的水资源承载力计算理论研究——以青海共和盆地水资源承载力研究为例[J]. 水资源与水工程学报, 2005, 16(3): 11-15.
[7] 惠泱河, 蒋晓辉, 黄强,等. 水资源承载力评价指标体系研究[J]. 水土保持通报, 2001, 21(1):30-34.
[8] 陈红, 回燕斌. 辽中南城市群水资源承载力分析[J]. 科技情报开发与经济, 2007, 17(10): 158-160.
[编辑] 洪云飞
10.3969/j.issn.1673-1409(N).2012.10.008
TV213.4
A
1673-1409(2012)10-N022-04

