自主招生数学试题中用“函数法”求不等式问题

● (常熟市中学 江苏常熟 215500)

自主招生数学试题中用“函数法”求不等式问题

●查正开(常熟市中学 江苏常熟 215500)

不等式问题在自主招生试题中占有重要的地位.随着新课程改革的实施，不等式的证明已成为理科学生的选学内容(选修4-5)，因此不少优秀学生得不到系统的训练，难以处理此类题目.为此本文给出解决不等式问题的有效途径——“函数法”，希望能对考生有所帮助.

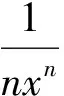
(2011年复旦大学自主招生数学试题)

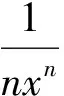
当x∈(0,1)时，f′(x)<0;当x∈(1,+∞)时，f′(x)>0;当x=1时,f′(x)=0.故

(2011年清华大学等七校联考数学试题)

解由已知得

整理得

从而

点评本题共有3个变量，将2个条件代入消元后可转化为一元二次函数问题.

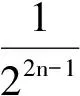
(2009年清华大学自主招生数学试题)

证明令A=x2n+y2n.由x,y>0且x+y=1知，y=1-x,x∈(0,1),即

A(x)=x2n+(1-x)2n,

从而

A′(x)=2nx2n-1+2n(1-x)2n-1(-1)=2n[x2n-1-(1-x)2n-1].

点评本题虽为二元问题但代掉一个即为一元问题，较易构造函数处理.运用本题的解法不难将这一问题进行推广：

推广1设x1,x2,…，xk∈R，且x1+x2+…+xk=1，则对于任意正整数n，有

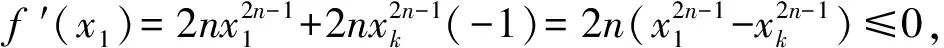
(2008年南京大学自主招生试题)

证明由题意知a,b,c对称，不妨设a≥b≥c，由a+b+c=1且a,b,c∈R+知

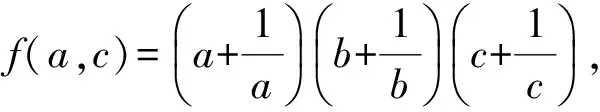
点评本题是三元条件不等式代掉一元即为二元问题可选一元为主变元，另一元视为常量.运用“函数法”可将问题推广为：

(2010年浙江大学自主招生试题)

f′(x1)<0.

点评本题是n元条件不等式，但只有n-1个独立变量，将一元作为主变元，n-2元视为常数，则最后一元与主变元有关.本问题还可用“函数法”作如下推广：

推广3设xi∈R+且x1+x2+…+xn=1,则

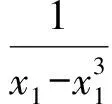
推广4若x1,x2,…,xn为小于1的正数且x1+x2+…+xn=1，n,m∈N*,n≥2，m≥3，则

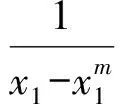
(2006年复旦大学推优、保送生考试数学试题)

综上可知，采用“函数法”证明不等式可规避传统不等式证明中灵活多变的方法和高难的技巧，弥补不等式知识的不足，强化函数(导数)的应用意识，使解题有明确的指向和固有的定式，思维流畅自然，使很多复杂的不等式证明题都能迎刃而解，对考生解答自主招生试题(竞赛题)具有广泛的适用性.