板坯连铸鼓肚变形行为分析
徐荣军
(宝山钢铁股份有限公司研究院,上海 201900)
0 前言
连铸铸坯坯壳的总应变主要由鼓肚应变、辊子不对中应变及矫直应变三部分组成。在坯壳的总应变中,由钢水静压力引起的鼓肚应变占的比重最大,若铸坯的坯壳应变过大,会引起铸坯内裂,甚至发生漏钢事故。同时,铸坯鼓肚变形造成的拉坯阻力在整个铸机总拉坯阻力中占的比重最大。因此,有效控制铸坯鼓肚变形量对控制总应变、防止铸坯缺陷、优化连铸机的辊列设计及对拉坯功率的选配具有十分重要的意义。
由于影响铸坯鼓肚变形量的因素十分复杂,很难求得问题的精确解。盛义平[1]总结了目前国内常见的计算坯壳鼓肚变形量的几个主要近似公式,公式大多把连铸坯壳视为承受均匀载荷的连续梁,认为坯壳的鼓肚变形完全是弹性的,将两夹送辊间坯壳视为一宽面固支,而窄面具有不同边界条件(将窄面视为固支边/简支)的承受均布载荷的等厚度弹性板,用差分方法求解鼓肚变形量。而在考虑蠕变变形对鼓肚的影响时又将其视为相当于一承受均布载荷的两端固支梁;后又有作者[2]将其视为两对边固支两对边简支的平板进行计算。部分研究者认为在二冷区几乎没有塑性变形,形成板坯鼓肚的主要因素是坯壳的高温蠕变[3]。
随着有限元商业软件的发展,有作者[4-6]对板坯连铸坯鼓肚变形的规律进行了二维和三维的仿真研究,这种方法也许能准确计算铸坯鼓肚量,但缺少普遍适用性,每一个工程问题要建立一个模型,工程实际应用中还是希望有一个普遍适用的解析解。
综上所述,鼓肚变形量的计算无外乎解析法(连续梁模型或平板模型)及有限元方法仿真两类,鼓肚变形量的计算解决了铸机设计中的辊间距选择问题,但对于铸机设计中拉坯功率大小选择即拉坯阻力计算问题,有限元方法仿真无能为力,基于连续梁模型的拉坯阻力计算[7]已有许多探讨,但关于平板理论的拉坯力计算很少涉及。本文试图从平板理论出发,考虑高温蠕变,推导出坯壳在钢液静压力和温度场的共同作用下的挠度解;从鼓肚变形能出发,推导出计算拉坯阻力实用的解析模型,以期更接近实际情况。
1 基本方程
根据坯壳凝固的实际工况,将坯壳视为一不均匀的温度场,且承受均布载荷(钢水静压力)的矩形薄板,由于板坯宽度远比辊距大,所以铸坯边界对内部影响根据圣维南原理可忽略不计。因此,其力学模型为:把坯壳视为一对边固支一对边简支,承受均布载荷p,坯壳温度场沿坯壳厚度方向线性变化的矩形板,计算模型如图1所示。
图1 平板挠度计算模型Fig.1 Calculation model of flat elastic deflection
平板的小挠度曲面微分方程为

边界条件
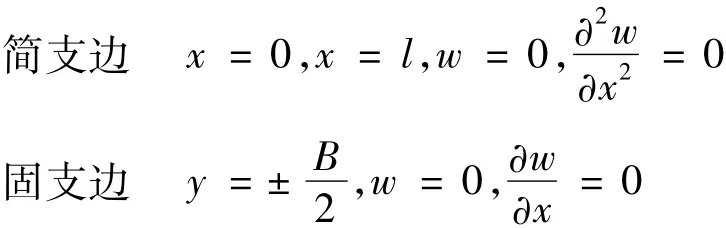
式中,B为坯壳承受静载荷的有效板坯宽度,mm;l为辊间距,mm;D为平板的弯曲刚度,壳厚,mm;S=■K t,其中,K为综合凝固系数,mm·min1/2,由试验测得,一般经验值为K=23~30,t为坯壳凝固时间,min;ν为泊松比。
根据曼内斯曼公司的实验,可以得出以下经验公式

式中,Tm为坯壳平均温度钢的固相线,Tf为坯壳表面温度,铸坯的表面为浇注速度,m/min;L为铸流长度,m。
2 挠曲方程的求解[8]
代入相应的边界条件,整理得挠曲面的近似解

应用双曲函数表就能计算任一点的挠度。最大挠度是在板的中心(x=l/2,y=0)处,在这里,最大挠度为
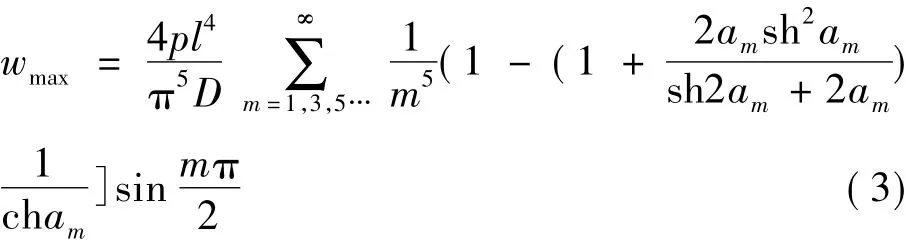
双曲函数的级数收敛得非常快,只取第一项就已足够精确。采用公式(3)可以把板坯的最大挠度表示成如下形式

其中,α为一数值因子,决定于板的二边长B/l,α的值可以在表1中查得。
对于板坯连铸,通常板坯宽度B远大于辊间距l,即B/l>2,所以α=0.002604。
以上推导常温下承受均布载荷平板的弹性变形挠度,而板坯是高温条件下在连铸机上运行的,因此必定受到高温蠕变[9]的影响。
铸坯的鼓肚与铸坯的应变直接相关,在钢水静压力的作用下,坯壳中的总应变ε为瞬时弹性应变εe和蠕变应变εc的叠加,因此铸坯的鼓肚变形也应该是这两部分的叠加。坯壳的总应变为
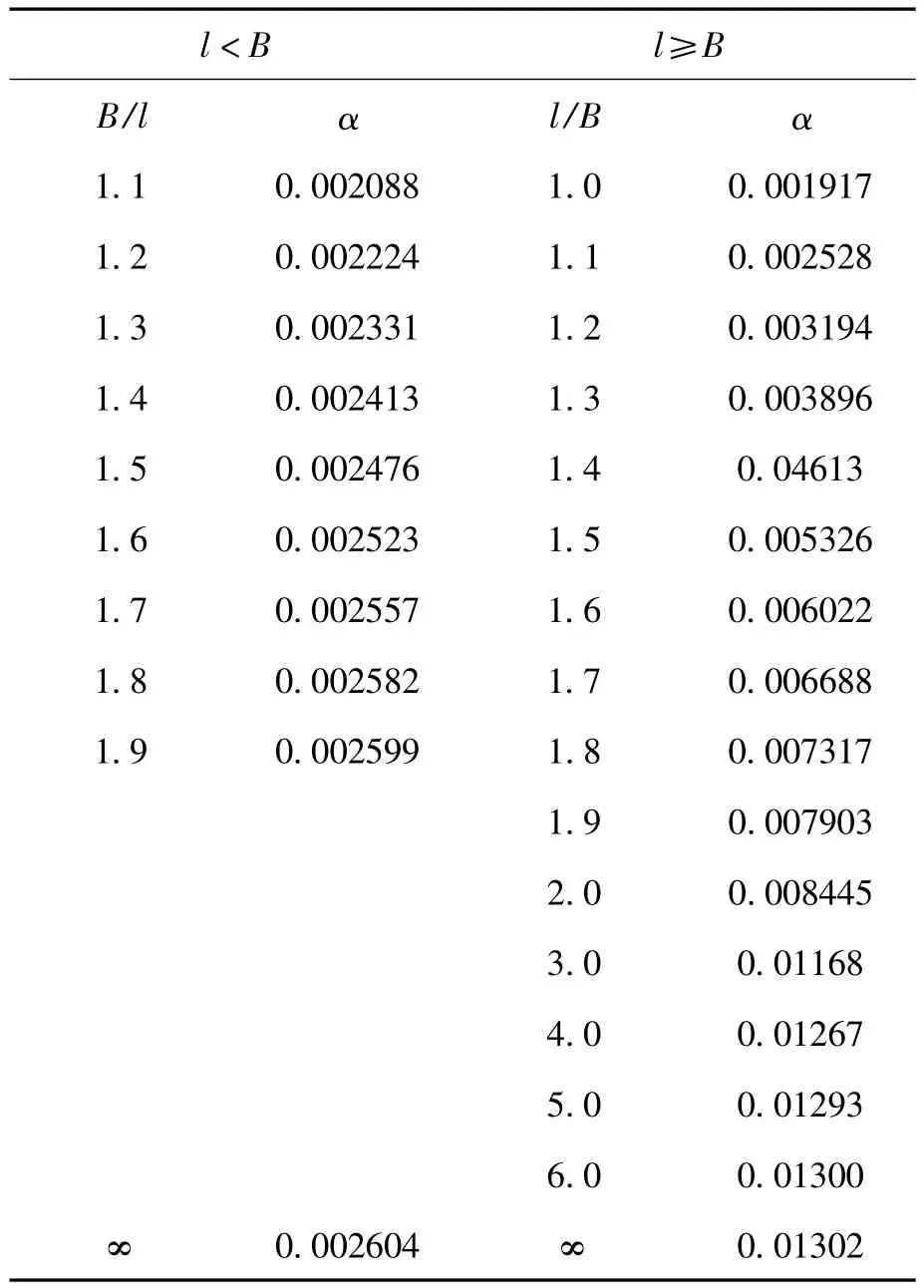
表1 承受均匀载荷的一对边简支另一对边固支矩形板的数值因子Table 1 Numeric factor α of a pair of simply supported edges and other two sides fixed supported rectangular plates which bear even load

由于,εe=σ/E,εc=cσntn,
取c=1/E,n=1,m=1/2;t为蠕变时间,min,t=l/v,v为拉坯速度,m/min;

相应的,根据挠度计算的叠加法原理,高温铸坯的挠度公式应该由式(4)修正为以下形式:
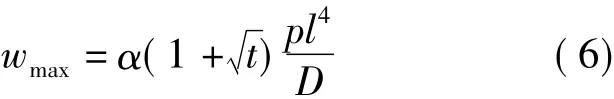
根据一对边简支一对边固支平板的对称性和式(3)的极佳收敛性,为简化计算,将铸坯的鼓肚曲面表示为
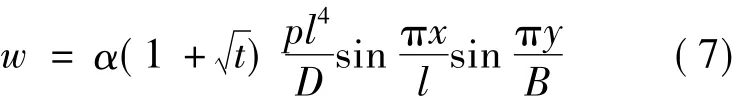
3 鼓肚阻力计算
3.1 矫平鼓肚拉坯阻力
如图2所示,鼓肚铸坯如要通过夹送辊,拉力F所做的功与辊子间坯壳鼓肚变形能的变化应相等,即

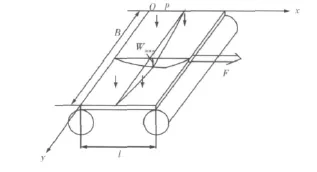
图2 矫平鼓肚拉坯阻力示意图Fig.2 Sketch of casting withdrawal resistance for flatting slab bulging deformation
根据文献[10],应变能的表达式为
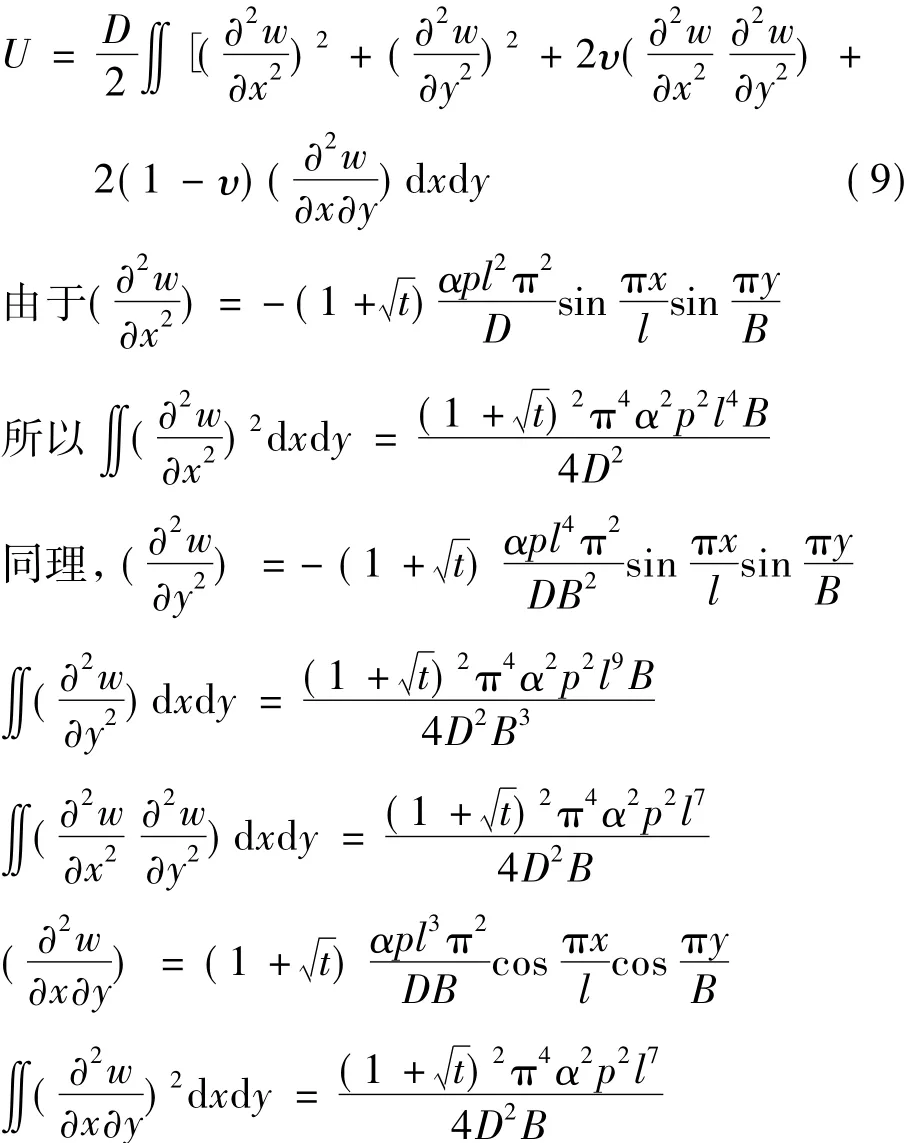
整理得,高温铸坯鼓肚应变能为
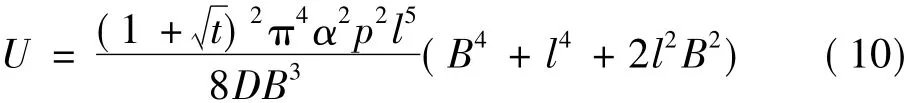
将t=l/v代入并对上式求偏导,即得第i对夹送辊矫平坯壳鼓肚阻力

若不考虑蠕变应变,铸坯鼓肚应变能为

对上式求偏导,即得第i对夹送辊矫平坯壳鼓肚阻力

式中,F1i为第i对夹送辊矫平坯壳鼓肚阻力,N;Pli为钢水静压力,N/m2;B为铸坯宽度有效宽度,m;D为平板的弯曲刚度,N·m;li为辊间距,m;v为拉速,m/min。
除了矫平鼓肚拉坯阻力外,铸坯通过二冷段还应有夹送辊在铸坯上的滚动阻力和夹送辊轴承转动阻力。
3.2 夹送辊在铸坯上的滚动阻力
铸坯经过第i对夹送辊时的滚动阻力F2i可按下式计算

式中,F2i为夹送辊在铸坯上的滚动阻力,N;f0为夹送辊与铸坯之间的的滚动摩擦系数,mm;Pi为第i个夹送辊所承受的压力,N,包括该夹送辊处的钢水静压力及该段铸坯重力沿垂直于拉坯方向的分量;Di为第i个辊子直径,mm。
3.3 夹送辊轴承转动阻力
第i对夹送辊轴承转动阻力F3i可按下式计算
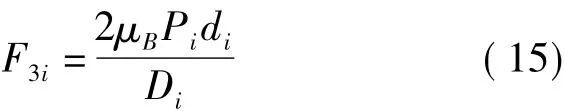
式中,F3i为第i对夹送辊轴承转动阻力,N;μB为第i对夹送辊轴承的摩擦系数;Pi为第i对夹送辊所承受的压力,N;Di为第对辊子直径,mm;di为第i对夹送辊轴承的内外径平均直径,mm。
4 计算、实测与讨论
图3为一实际工程中已有方法和本方法计算的最大鼓肚变形量计算对比。计算条件:铸机坯宽1650 mm,厚度235 mm,铸机长度41.2 m,半径R=9500 mm,拉速1.8 m/min,计算铸坯从结晶器出口直到到凝固完毕的最大鼓肚量,并与目前国内常用的鼓肚量计算模型算的结果[11]相对比。结果发现本模型计算的鼓肚量是现有模型的3倍左右。
表2为计算的拉坯阻力与实测值比较。为了验证计算模型的准确性,用已有的摩擦阻力计算行计算,除了二冷段的拉坯阻力外,其他部分计算采用文献[7]同样的模型计算,因此其值是一样的。同时对实际铸机进行实测。由于实测是通过拉坯电机的实际输出力矩得到,因此只能得到总的拉坯阻力,不能显示某分项拉坯阻力大小。计算时不考虑轻压下且实际测量中轻压下也不投入,排除了轻压下附加拉坯阻力的干扰。本模型计算结果和实测值比较呈正偏差+10.1%,而原有模型和实测值相比呈负偏差-59.9%。
由于最大鼓肚量无法直接测量,亦无法直接与实际情况比较,但可间接通过拉坯阻力进行比较。从表2看到,无论采用哪种计算模型,二冷段因钢水静压力造成鼓肚引起的拉坯阻力都占绝对多数,由于铸坯鼓肚量的大小决定了拉坯阻力的大小,说明本模型在计算最大铸坯鼓肚量和拉坯阻力方面比原有模型更接近实际情况。
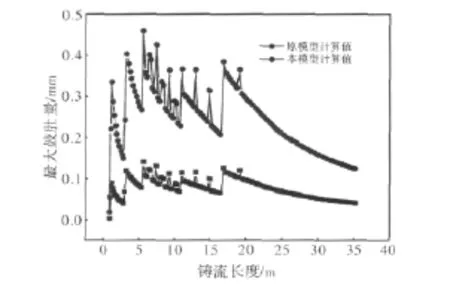
图3 最大鼓肚变形量计算值对比Fig.3 Contrast of calculated values of maximum bulging deformation

表2 连铸机的拉坯阻力Table 2 Casting withdrawal resistance of CCM

/kN 2.712 0.146 2.712 0.296总拉坯阻力/kN 1482.257 540.400 1346.600偏差水平段阻力/% 10.074 -59.869
5 结论
从平板理论出发考虑高温蠕变推导出坯壳在钢液静压力和温度场的共同作用下的挠度解。从鼓肚变形能出发,推导出计算拉坯阻力的计算模型。通过工程实例计算和现场拉坯阻力实测,说明本模型在计算最大鼓肚量和拉坯阻力方面其结果比现有模型更准确。其方法可用于连铸机的辊列设计计算及连铸工艺制订。
[1] 盛义平,孙蓟泉,章敏.连铸板坯鼓肚变形量的计算[J].钢铁:1993,28(3):20-25.
[2] 孙蓟泉,盛义平,张兴中.连铸板坯的鼓肚变形与应力分析[J].钢铁研究学报:1996,8(1):11-15.
[3] 盛义平,张晓春.连铸坯壳在二冷区内的蠕变弯曲[J].燕山大学学报:2004,28(1):33-35.
[4] 焦晓凯,秦勤,吴迪平,等.板坯连铸铸坯鼓肚变形的仿真研究[J].冶金设备:1997(1):9-12.
[5] 宁振宇,吴迪平,秦勤,等.板坯连铸三维鼓肚变形仿真研究[J].冶金设备:1997(2):5-8.
[6] 罗秉臣.连铸板坯坯壳鼓肚变形量的有限元分析[J].钢铁研究学报:1995,7(1):91-97.
[7] 盛义平,郭普学.弧形板坯连铸机的拉坯阻力[J].重型机械:1992(6):20-23.
[8] S.铁摩辛柯 S.沃诺斯基.板壳理论[M].板壳理论翻译组,译.北京:科学出版社,1977.
[9] Gvlin T F,Hacon J,Hazra L K,et al.The Creep Properties of Carbon Steel to B.S.150-161 and 224 Grades[A].British Steelmakers Creep Committee.The Presentation of Creep Strain Data[C]London:Battersea,1972,37-60.
[10] 刘鸿文,林建兴,曹曼玲.板壳理论[M].杭州:浙江大学出版社,1987:83-84.
[11] 曹广畴.现代板坯连铸机[M].北京:冶金工业出版社,1994:102-110.

