南海海浪业务化数值预报系统检验

周水华，俞胜宾，梁昌霞，冯伟忠，吴迪生

（国家海洋局南海预报中心，广东 广州 510310）

1 引言

20世纪40年代，美国利用天气图预报海浪，通过海浪经验统计预报方法、半经验半理论波谱预报方法和能量预报方法等推算波高，再综合分析和校正，带有较强的经验性。20世纪50年代初，基于能谱概念上的分析模拟成为主要研究途径，经历了近40年的研究，到上世纪80年代WAM模型的推出[1]标志海浪数值预报模型已经进入第三代。第三代海浪模型是采用基于能量守恒原理的能量平衡方程波浪谱模型,它是各种物理过程考虑最完善，最少经验假定的波浪模型。该模型中考虑了水深变化、背景流等对波浪传播的影响，同时考虑了包括风摄人波动能量、白浪耗散、水深变化导致的波浪破碎、底摩擦耗散、波一波非线性相互作用等物理过程。上述各物理过程用不同的源函数表示，有效地简化了波浪场的动力学过程,随着对各种物理过程的深入认识，参数化的形式不同,模型的表现形式也不一样。目前，国际上广泛应用的第三代海浪数值模式有WAM，WAVEWATCHIII和SWAN等,尤其是海浪的业务化预报使用的多是以上三种模型。如美国气象局、台湾中央气象局采用WAVEWATCHIII,欧洲气象中心（ECMWF）挪威气象中心采用WAM,英国气象局、比利时国家气象研究院采用WAM和SWAN等。我国从事海浪业务化预报的主要有国家海洋局下属的国家海洋环境预报中心、北海预报中心、东海预报中心以及南海预报中心。国家海洋环境预报中心采用WAM和WAVEWATCHIII模型进行全球和大洋的海浪业务化预报，采用SWAN模型进行中国海的海浪业务化预报；北海预报中心和东海预报中心均采用SWAN模型进行各自管辖海区的海浪业务化预报。但从查阅的文献来看，暂未见到上述国内预报机构的海浪业务化预报系统的检验结果。南海预报中心于2008年建立了以MM5中尺度气象模型和WAVEWATCHIII海浪模型为基础的南海气象海浪业务化数值预报系统，受观测资料的限制，该系统建立之初仅利用零星观测资料对模型进行调试和参数校正后，就投入业务化运行，因此对于该系统在南海预报效果还有待更多检验。最近两年，随着南海浮标观测资料的增加，有条件对该预报系统在南海的预报效果进行较为系统的检验。本文利用南海北部的三个浮标观测站近两年的观测资料对该系统进行检验，发现预报与观测之间的差距，为系统下一步的改进奠定基础。

2 南海海浪业务化数值预报系统

2.1 总体框架

南海海浪业务化数值预报系统包括主系统和辅助系统两个子系统，主系统用于进行数值计算，辅助系统的功能是对数值预报结果进行后处理。主系统共由两个核心计算模块组成，MM5中尺度气象模式（为海浪计算提供上边界条件）和WW3（WaveWatchIII）海浪预报模式。辅助系统为交互式操作平台，可以浏览和生成不同形式的数值预报产品，并且该子系统具有开放性，能进行升级优化。该系统在超级计算机集群系统中采用MPI并行模式每天早晚两次自动启动预报作业，在启用12个计算节点的并行运算条件下，从数据下载到数据的后处理，可在3 h内完成一次预报（预报时长72 h），其中海浪预报与后处理耗时约半小时，预报结果转存至互联网（http://58.249.58.22/），供预报值班员和公众参考。

2.2 预报区域及相关参数设置

做为一个业务化数值预报系统，预报结果的可靠性和预报的时效性是两个最重要的考核指标，经过多次的实验和比较后，确定模型的计算区域和相关参数设置如下：

MM5中尺度气象模块：模式框架取MM5V3版本，预报区域分为两重嵌套，大区域范围71.91°—156.51°E。15.68°S—53.91°N，空间步长45 km，小区域范围 98.48°—129.66°E，0.23°—27.66°N，空间步长15 km。模式垂直分层为不等距23层，顶层取100 hPa。大小网格的地形资料分别取自全球10′和5′的地形资料。初估背景场和模式侧边界采用美国国家环境预报中心（NCEP）的GFS（全球预报系统）数据。积云对流参数化选用Burk-Thompson方案，边界层参数化方案采用MRF PBL边界层方案。

WW3海浪模块：采用WaveWatchIII 3.14版本，计算范围见图1（0°—41°N，99°—140°E），空间分辨率为6′×6′，时间步长600 s，方向分辨率为30°，频率分级采用对数30级。地形数据来源于NOAA的etopo2v2，由于etopo2v2对近岸水下地形的观测误差较大，因此，近岸水深数据由中华人民共和国海军航海保证司令部出版的海图读取。上边界条件使用中尺度气象模式MM5输出的海面10 m高度风场。初始场采用热启动模式，由上一次的预报结果提供，其它参数采用模型的默认值[2]。

3 统计检验方法

采用国家海洋局在南海布放的3个浮标（位置见图1）的观测结果对数值预报结果进行检验，统计检验时间（2010年3—11月，2011年3—11月），统计检验要素包括有效波高和平均周期，基本统计检验参数有绝对误差、相对误差、平均绝对误差、平均相对误差。

为分析预报误差的主要分布区间，进行了各级误差出现概率统计：

为分析预报值与观测值之间是否存在系统性的偏差，对观测值和预报值进行了线性回归分析。

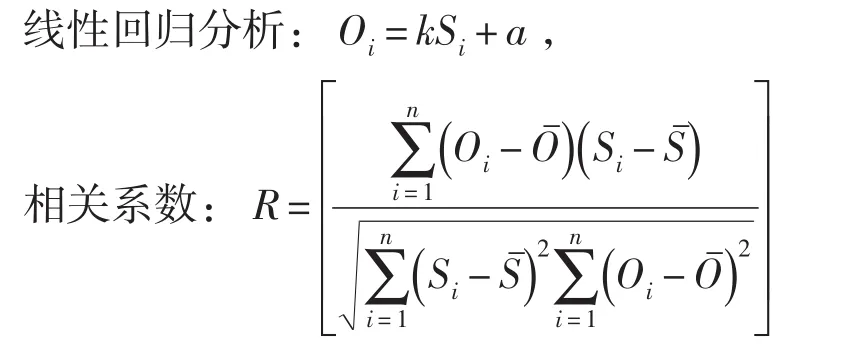
Oi：观测值， Si：预报值，：观测平均值，Sˉ：预报平均值，n：统计样本总数，m：AEi≤x的样本数，l：REi≤x的样本数。

图1 海浪预报范围与浮标位置

4 检验结果分析

4.1 24 h、48 h、72 h预报误差比较

从有效浪高的统计检验结果来看，各站24h、48 h、72 h预报的MAE都小于0.5 m，MRE小于35.6%， MAE和MRE都表现为24 h预报＜48 h预报＜72 h预报，但差别不大。各站24 h预报MAE在0.30—0.34 m，MRE29.1%—25.8%，三站平均MAE为0.30 m，MRE为27.0%。各站48小时预报MAE在0.33—0.44 m，MRE34.1%—27.7%，三站平均MAE为0.38 m，MRE为30.5%。各站72小时预报MAE在0.41—0.48 m，平均相对误差33.9%—37.7%，三站平均MAE为0.45 m，MRE为35.6%。

平均周期的各站24 h、48 h、72 h预报的MAE都不超过0.78 s，平均相对误差不超过13.7%，MAE和MRE都表现为24 h预报＜48 h预报＜72 h预报，差别比有效波高更小。各站24 h预报MAE在0.60 s—0.65 s，MRE10.5%—11.2%，三站平均MAE为0.62 s，MRE为10.8%。各站48 h预报MAE在0.65 s—0.71 s，MRE11.3%—12.3%，三站平均MAE为0.68 s，MRE为11.7%。各站72 h预报MAE在0.77 s—0.78 s，平均相对误差13.3%—13.7%，三站平均MAE为0.78 s，MRE为13.5%（见表1）。

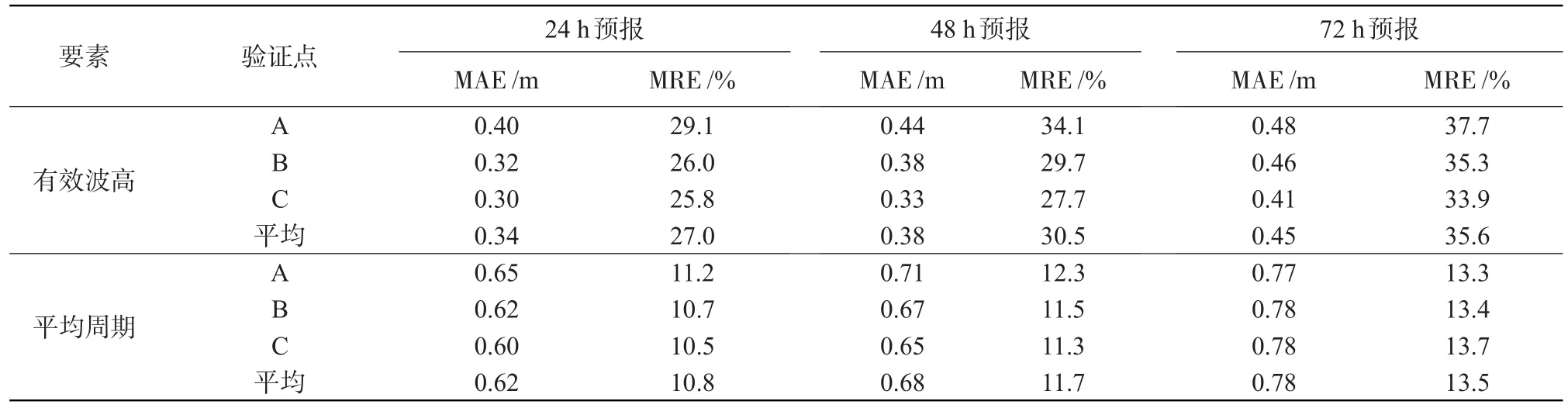
表1 预报误差统计

表2 各级预报误差出现概率统计

4.2 预报误差的区间分布

将各统计样本的绝对误差AEi（相对误差REi）从0开始，以0.1（10%）为间隔进行等间距递增，分别统计各级误差出现概率，绘制各级误差出现概率图（见图2—3），图2和图3显示各级误差出现频率为高度近似对数分布，说明大误差的出现概率较小误差的出现概率低。

表2显示有效波高24h、48h、72h预报AEi≤0.5m的出现概率都在70%以上，24 h预报REi≤30%的出现概率为64.1%，48 h和72 h预报REi≤30%的出现概率都不足60%。平均周期 24 h、48 h、72 h预报AEi≤1.0 s的出现概率都在71%以上，24 h预报REi≤20%的出现概率为86.3%，72 h预报REi≤20%的出现概率也可达77.4%。平均周期24 h、48 h、72 h预报REi≤30%的出现概率都在93%以上。

4.3 预报误差的季节变化

图2 有效波高各级预报误差出现概率图

图3 平均周期各级预报误差出现概率图

表3 各月24 h预报误差统计表

表4 观测值与预报值相关分析结果

从有效波高24 h预报误差统计来看（见表3），除A站的2月份，预报MAE较大之外，其它各站各月的预报MAE都小于0.5m，且MAE没有明显的季节变化。各站预报的MRE都具明显的季节变化，10月和11月预报MRE显著小于其它各月，4—7月误差较大，误差最大值在5月。5月份预报MRE三站平均为34.1%，以A站最大，为39.8%，C站最小为30.6%。10月和11月的MRE三站平均分别为14.0%和11.6%。B、C两站11月的预报误差小于10月，A站预报误差最大，且10月和11月预报误差相当。造成这种现象的原因与气象模型对天气系统预报的准确率有很大的关系。现有的中尺度气象模型对于大尺度的稳定气象过程（如东北季风）预报效果要好于中小尺度的气象过程（如热带气旋），对于频繁变化的气象过程刻划的也不够理想。因此在4—7月受气象模型对热带气旋和天气系统变化过程预报效果相对欠佳的影响，海浪的预报结果也不如其它季节理想，每年的12月—翌年2月南海受东北季风控制，由此可推断12月、1月和2月的预报误差小于或等于11月，南海海浪业务化数值预报系统实际的年平均预报相对误差也应该小于表1的统计结果。

平均周期预报误差的季节变化与有效波高不尽相同，预报MRE和预报MAE呈相同的季节变化规律，10月和11月显著小于其它各月，4月、8月和9月则较其它月份大（见表3）。

4.4 预报与观测的相关性分析

从回归分析的结果来看（见图4），无论是有效波高还是平均周期，预报值与观测值都呈明显的线性相关，有效波高预报值和观测值的相关性高于平均周期。以有效波高24 h预报的相关度最高，相关系数0.85，属高度相关，其它的相关系数介于0.61—0.77之间，属中度相关。表4显示相关系数K都小于1，总体来说预报值相对于观测值偏大，相关系数随预报时效的增长而减小，24 h预报＞48 h预报＞72 h预报，反应了预报值与观测值随预报时效的增长相关度呈现递减的趋势。

图4 有效波高散点图

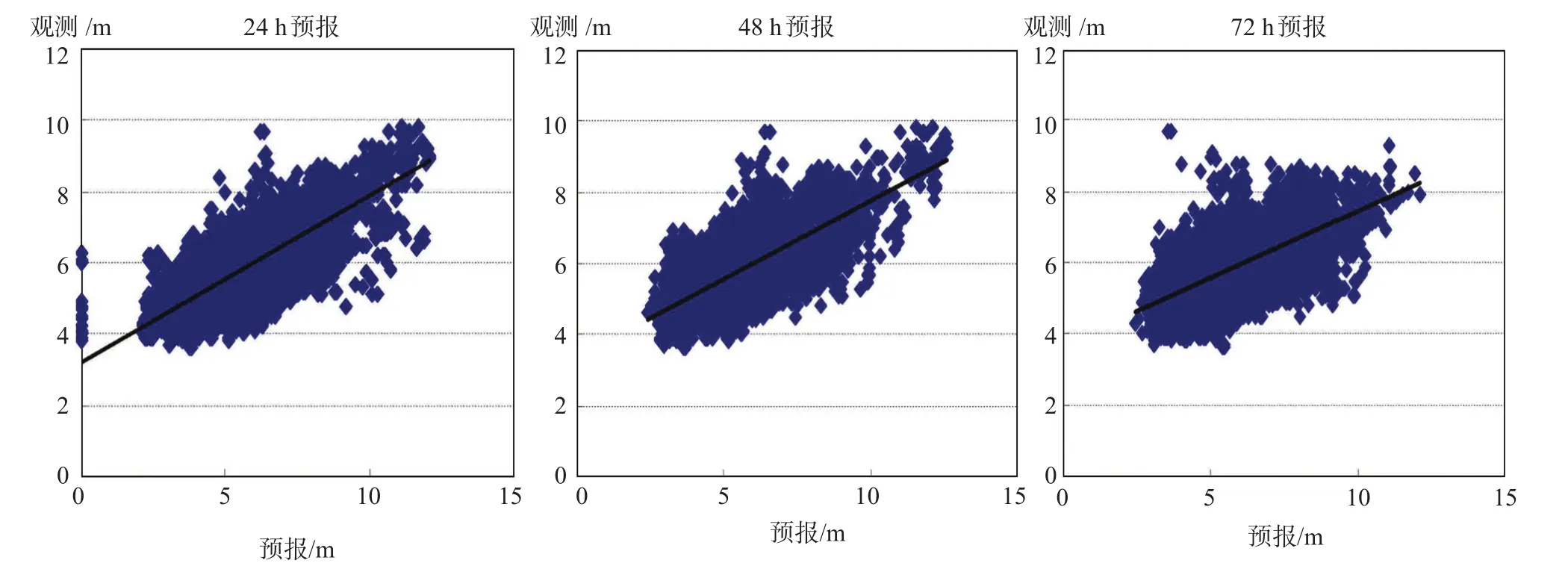
图5 平均周期散点图

从预报值与观测值的散点图来看（见图5），对于浪高很小的涌浪，模型的表现效果较差，南海的周期通常都在3 s以上，即使在有效浪高仅0.1 m的情况下，平均周期仍然可达到4—6 s，甚至更长。对于这一类型的海浪，模型是难以预报出来。

5 结论

通过计算预报值和观测值的绝对误差、相对误差、平均绝对误差、平均相对误差、各级误差出现概率等统计参数和线性回归分析，对南海海浪业务化数值预报系统进行系统检验。形成主要结论如下：

（1）有效波高和平均周期的预报误差随预报时效的增长而增大，即24 h预报＜48 h预报＜72 h预报；

（2）平均周期的24 h、48 h、72 h预报平均绝对误差小于0.8 s，24 h、48 h、72 h预报相对误差分别为10.8%、11.7%和13.5%；有效波高的24 h、48 h、72 h预报平均绝对误差小于0.5 m，24 h、48 h、72 h预报相对误差分别为27.0%、30.5%和35.6%；

（3）有效波高和平均周期的预报误差有明显的季节变化，10月和11月的预报误差显著小于其它各月，根据误差的季节变化推断12月—翌年2月的预报误差不超过11月，实际的年平均绝对误差比统计值要小；

（4）回归分析结果显示预报值与观测值存在中度高度线性相关，随着预报时效的增长相关度逐渐递减，总体来说预报值较观测值偏大。

以上检验结果显示，该系统的预报误差在可接受的范围之内，基本能满足业务化预报的要求，尤其是冬季的24 h预报，预报误差小，预报结果具有很高的应用价值。但该系统的预报效果与欧洲气象中心等先进国家的预报系统比较还存在较大的差距[3]。

[1]WAMDI Group.The WAM model—a third generation oceanwave prediction model[J].Journal of Physical Oceanography，1988，18：1775-1810.

[2]Hendik L.Tolman.User Manual and system documentation of WAVEWATCH III version 3.14.U.S:Environmental Modeling Center Marine Modeling and Analysis Branch[R],2009,91-194.

[3]Jean-Raymond Bidlot.Reports on intercomparison of operational wave forecasting systems.The Joint Technical Commission for Oceanography and Marine Meteorology(JCOMM) [R/OL],2009-.