露天矿生产车辆调度的优化选择

刘浩洋，嵇启春，许苗苗，贾 雷

（1.西安建筑科技大学， 陕西 西安 710055；2.陕西陕煤澄合矿业有限公司王村煤矿，陕西 渭南市 715306）

露天矿生产车辆调度的优化选择

刘浩洋1，嵇启春1，许苗苗1，贾 雷2

（1.西安建筑科技大学， 陕西 西安 710055；2.陕西陕煤澄合矿业有限公司王村煤矿，陕西 渭南市 715306）

露天矿车辆优化调度问题，关键是如何分配和调度现有条件下的卡车和电铲，使设备的利用率达到最大，从而降低采矿成本。根据露天生产的实际要求，运用运筹学中的目标规划的方法，建立车辆调度的优化模型，利用Lingo11软件进行计算；利用卡车编队运输、卡车转移运输的思想和贪心算法，得出一种最优的调度方案。研究表明，优化结果能符合实际生产需求。

车辆调度；目标规划；Lingo；实时调度；露天矿

0 前 言

露天矿是一个以采掘为中心，以运输为纽带的大型生产系统，卡车运输在露天矿企业中占有重要地位。卡车运输的任务是将采场采出的矿石运到选矿厂、破碎站或贮矿场；把剥离的岩土运送到排土场；将生产过程中所需要的材料运送到作业地点。在我国，大多数高产量的煤矿都是露天开采，这些露天矿主要采用单斗—汽车开采工艺。对于汽车运输的露天矿，随着开采深度不断加大，会使运输距离增加，运输周期增长。大型露天矿开采中，矿山运输的基建投资约占总投资的40%～60%，运输成本占矿山总成本的35%～45%左右，运输能耗占矿山总能耗的40%～70%［1］。车辆优化调度是降低采运设备非生产时间、提高生产效率，从而降低整个采矿成本的行之有效的办法。国内外实践表明，只要能使产量提高3%～5%，就足以证明采用计算机控制卡车调度系统是经济合理的，事实上这种提高的幅度往往高达6%～32%［2］。

1 车流多目标规划模型

采用目标规划的方法建立车流规划的多目标规划模型，露天矿生产要求在不同的目标决策环境中，对产量、品位、产量均衡等多目标进行权衡。通常来说，由于多目标优化问题的各个目标往往存在着相互矛盾的情况，所以多目标优化问题难以找到一个让所有优化目标都同时达到全局最优解［3］。因此，多目标优化问题的求解主要通过求得一个满足各项约束条件的可行解来实现。为了求得这样一个可行解，多目标优化算法的主要思路都是将多目标优化问题转化为多次求解的单目标优化问题［4］。

露天矿车辆调度是具有许多不确定因素的多目标规划问题，这些目标都以提高经济效益为核心，这里选择利用现有的车辆，使总产量最大（岩石产量最大）和总运量最小。根据实际情况，以总运量最小为主要目标，总产量最大（岩石产量最大）为约束条件，这样就能把多目标问题转化为一个以主要目标为目标的单目标规划［5］。

1.1 模型假设

（1）运输过程中卡车不会出现堵车现象，路况理想，卡车以恒速行驶；

（2）电铲和卡车在一个班次内可以不停的工作，如中途不会出现机器故障等；

（3）一个班次内卸点、铲位的位置不会变化；

（4）卡车在装卸时不会出现等待；

（5）卡车的路线可以不固定，当其在一条线上完成了任务之后可以到其他线上去帮助别的车辆运输；

（6）卡车可以在一个班次内运输不同的货物，但每次只能运一种，当某个铲位的矿石或岩石量低于卡车载重时，卡车不再运输。

1.2 约束条件分析

（1）满足每个卸点的产量要求：

（2）第i个铲位所运输出去的矿石总量不能大于该铲位的矿石总量：

（3）第i个所运输出去的岩石总量不能大于该铲位的岩石总量：

（4）铲位所装车次小于一个班次内可能的电铲最多装车数：

（5）卸点所卸车次小于一个班次内可能的最多卸载车数：

（6）铲位i到卸点j实际运行卡车次数小于等于一个班次内铲位i到卸点j的最大车次数：

（7）卸点的矿石满足品位要求：

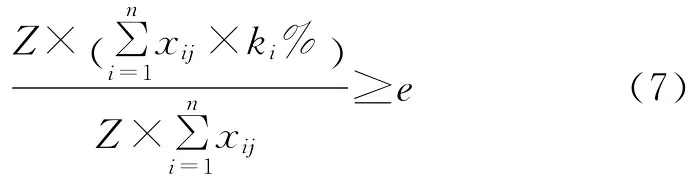
（8）每条线路上的运输次数为非负整数：

其中：n为铲位个数；m为卸点个数；e表示品位限制；xij为铲位i与卸点j之间的实际运行的卡车次数；dij为铲位i与卸点j之间的距离；ki为铲位i的矿石量；yi为铲位i的岩石量；ki%为铲位i的矿石的平均矿含量；yij为铲位i到卸点j路线上最多能同时运行的卡车数；zij为铲位i到卸点j路线上一辆车最多能运行的次数；Tij为铲位i到铲位j路线上平均一个周期所需时间；Z为一辆卡车的载重；fj为卸点j的任务需求量；cmax为电铲一个班次可装的最多车次数；xmax为卸点一个班次可卸载的最多车次数。

1.3 目标模型

利用现有的车辆，获得最大的产量（岩石量优先）；在产量相同的情况下，取总运量最小的解。目标函数如下：

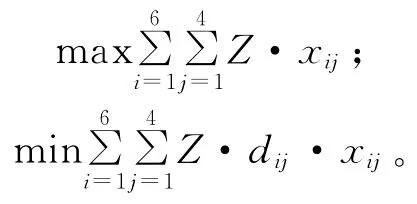
2 调度模型的应用

某稀有金属露天矿有6个铲位，4个卸点，包括卸矿点1、卸矿点2、卸矿点3和岩场1。某集团公司车辆在一个班次内所承担的运量大约为：卸矿点1为0.26万t、卸矿点2为0.27万t、卸矿点3为0.14万t、岩场1为0.71万t。现有电铲6台，载重45t的卡车30辆。卡车的平均速度22km/h，卸点品位要求在0.130%，一般在0.125%～0.135%之间即可。通过GPS测得个铲位和卸点之间的距离如表1所示，各铲位的矿岩量及品位见表2。

表1 各铲位和各卸点之间的距离 km

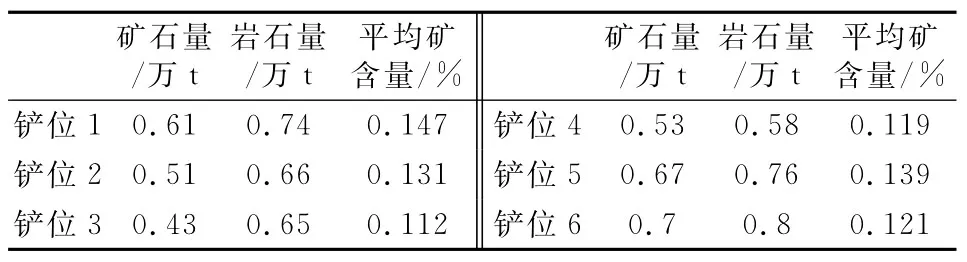
表2 各铲位矿石、岩石数量和矿石的平均矿含量

求解最佳派车方案，车型和车辆数一定，要使车辆的利用率达到最大，即总产量最大（岩石产量最大）和总运量最小。用软件Lingo11编程，运输最大车次576车次，其中运矿石418车次，岩石158车次；可得最大产量为25920t，最小运量为55500.7 t·km。卡车运输次数如表3所示。

表3 卡车运输次数

针对卡车不能等待的理想情况，应用卡车排队运输和卡车转移运输的思想。卡车排队运输是让卡车排队在同一线路上运输（卡车数满足最大容车辆限制），保证前一辆车和后一辆车始终间隔5min，不会发生卡车等待的情况。卡车转移运输是一队卡车在保证运完自己线路上的运量还有富裕时间，转移到其它线路上运输，此时只需考虑转移到另一条线路上后不会和那条线路上已有的卡车发生等待。派车问题其实是组合优化，先将满足整车运输的任务安排相应的整车在固定线路上，运输剩余的不满足整车运输任务的零碎任务时，使用贪心算法求解。最终，卡车调度安排最优组合的其中一种见表4。

表4 固定卡车分配

表4中，15（2、3、4、5）表示2、3、4、5号卡车只在铲位1到岩场上各运输15次；13［21］、5［21］表示21号车在铲位1到岩场运输13次，在铲位5和卸矿点1运输5次，这样才能充分利用卡车工作时间，即卡车转移思想；其余相同。最终卡车没有分配完，由于实际情况中存在很多随机的影响因素，所以剩余几辆卡车备用也是合理的。该计算结果是车辆实时调度的依据，利用GPS实时调度系统使车辆运行尽量满足以上方案，同时满足线路上的运行卡车数不大于最大运行车数的限制。

3 总 结

随着现代生产力的发展，国家对矿产资源的需求也在逐年递增，原有的车辆运输调度很有可能制约着露天矿开采运输能力。本文对露天矿实际情况做了简单分析，假设在理想情况下，当车辆数一定时，以矿石产量最大为目标，满足产量为约束条件，每个铲点到每个卸点的运输车次数为决策变量，求出各路线上车辆调度情况。

［1］ 汪为平，蔡鸿起.我国大型露天矿运输技术现状及发展对策［C］//第3届冶金矿山采矿选矿技术进展报告会论文集.马鞍山：马鞍山矿山研究院，1997.

［2］ 郝全明，陈丽林，孟祥铭.露天矿生产车辆调度的最优化选择［J］.采矿技术，2011，11（1）：55－57.

［3］ 徐玖平，李 军.多目标决策的理论与方法［M］.北京：清华大学出版社，2005.

［4］ 谢邦鹏，张雪敏，梅生伟，等.HAVC系统的多目标趋势化优化序贯式算法及东北电网应用［J］.电工电能新技术，2008，27（1）：10－15.

［5］ 蒋安松，张 强，黎雪松，等.露天矿生产车辆调度的最优化模型［J］.四川理工学院学报（自然科学版），2004，17（3）：104－108.

2012－06－29）

刘浩洋（1988－），男，河南许昌人，在读硕士，从事系统工程研究，Email：185886404＠qq.com。