含交易费用的组合投资模型的动态规划解法*
李 萌
(中国海洋大学,山东 青岛 266100)
1 引言
证券投资是近年来我国投资市场的热点。作为一种风险投资,其收益必将伴随着相应的风险。通常,高的收益都是与高的风险相伴随。一个理性的投资者希望能获得尽可能多的收益,同时风险尽可能低。显然,这两个目标是相互矛盾的。因此,为了减少风险获取较为稳定的收益,投资者一般选择将资金分散到不同资产进行组合投资。而如何分配资金到不同的投资项目中,使得在风险一定的情况下收益尽可能的高或者是收益一定的情况下风险尽可能的低成为投资者关注的焦点。20世纪50年代后,马科维茨(Markowitz)等人提出的投资组合理论,正好可以从数学角度进行解答。
一般金融资产具有如下特征:流动性、风险性、收益性、无限可分性。而上述特征决定了资产组合收益的特殊性:即在一个有效的市场中,某证券下一期的预期价格等于当期价格加上下一期预期报酬。这说明投资组合的各阶段的状态满足无后效性,即投资过程的过去历史只能通过当前的状态影响它的未来,因而满足构造动态规划模型的条件。[1]
利用动态规划研究投资组合问题的方法已有一些研究[2-4]。在文献[2]中,作者对均值-方差模型建立一种动态规划模型和递推算法。文献[3]建立了总风险控制下的以最终的总收益最大化为决策目标的资产投资组合模型,并利用动态规划的方法求得模型的整体最优解。文献[4]利用动态规划方法解决带交易费用的均差模型,给出了有交易费用均差模型的解析解。本文在考虑交易费用的前提下,用动态规划的方法求解组合投资模型。
2 模型的建立
设投资者现有资金M,可在一个时期内投资于市场上的n种资产A1,A2,…,An或存款银行A0。假定Ai之间相互独立。通过对历史数据的统计,得到各资产Ai有收益和损失两种情况,收益时平均收益率为ri,损失时平均亏损率qi,且损失的概率为si。假定在该投资时期内Ai收益损失情况保持不变。银行存款A0的利率为r0且无风险(q0=0)。考虑到我国证券市场的交易费用的收取按“手”为单位,在本模型中规定购买资产Ai的交易费是分段函数:不购买不收费,每单位证券的收费率为pi,但当购买量不足ui时,交易费按购买ui计算。因此,购买Ai的收益须减去交易费之后得到净收益。由于一只资产购买过多可能会带来不可估量的损失且与组合投资的理念不符,影响判断,故当购买量超过di时,资产Ai无法继续购买。在本文中,我们以投资各个Ai的风险损失和来度量总体风险。设xi表示购买资产Ai的资金(1≤i≤n),x0为银行存款。则交易费可表为:

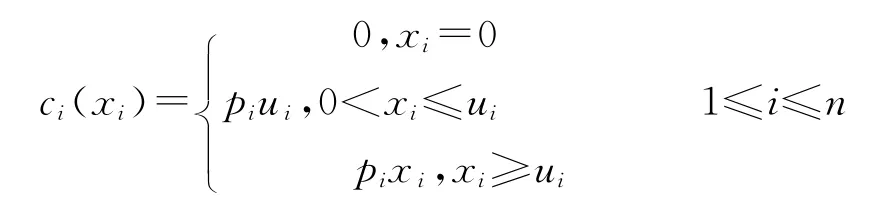
投资组合x=(x0,x1,…,xn)收益时的每种投资收益为xiri-ci(xi),而损失时的每种投资损失为xiqi+ci(xi),则数学期望收益为

从而得到如下的投资组合模型(I)

由于ci(xi)是分段线性函数(在x=0处不连续),模型为非线性规划问题,下面利用动态规划来求解。
3 模型的动态规划解法
在模型(I)中,对n+1种资产的资金分配看成n+1阶段决策过程,其中xi作为第i阶段决策变量,从第0阶段到第i阶段所分配的资金记为li,作为第i阶段的状态变量。那么,n+1阶段所分配的总资金为ln+1=M,且状态转移规则为li-1=li-xi-ci(xi)。
当状态变量li给定时,决策变量xi取值范围成为第i阶段的决策集,记为Di(xi)。根据上面的模型,有:

在每阶段决策时都要求xi∈Di(li),故而其成为一个动态规划。
根据前面分析,用顺推法求解。设函数fk(l)为直到第k阶段,投资额不超过li的最大收益,有:

根据动态规划最优原理,得到最优值函数序列满足如下递推:

决策集Dk(l)表示为:

由动态规划的理论可求的模型(I)的解。
4 讨论
(1)Ai的收益损失是根据历史经验所得,因此要求市场有很强的有效性,对于我国目前还不尽完善的金融市场现状,解释起来有点乏力。
(2)该文主要是从数学推导,没有考虑实际投资中各种其他因素的影响,会使得该模型在实际应用中的效果打折扣。
(3)实际操作中,为了规避风险,投资者会进行多期连续且有关联的投资,因此该模型仍然有待于进一步的完善。
[1]张梦乔.基于动态规划的投资组合优化研究[J].时代金融,2011,(11):155-156.
[2]林浩.投资组合问题的动态规划方法[J].运筹与管理,2000,9(3):102-106.
[3]陈国华,廖小莲,吴娜.投资组合模型的动态规划解法[J].统计与决策,2012,(5):85-87.
[4]花秋玲,苏孟龙,吕显瑞,等.带交易费用投资组合问题的动态规划方法[J].吉林大学学报:理学版,2009,47(5):893-898.

