基于约束最小二乘估计的影响分析

周兰萍，夏海峰

(1.江苏省扬州中学教育集团树人学校，江苏 扬州 225000;2.江苏省扬州市邗江区公道中学，江苏 扬州 225119)

本文考虑如下线性回归模型

y=Xβ+e,E(e)=0,Cov(e)=σ2In

(1)

其中y是n×1的观测向量，X为n×p的已知设计矩阵，β为n×p未知参数向量，e为随机误差向量。并假设

Aβ=b

(2)

是一个相容线性方程组,其中A为k×p的已知矩阵,且秩为k,b为k×1维已知向量.

由于线性回归模型(1)是统计学中最重要的模型之一，所以众多的学者对其进行大量而深入的研究(如文献[1～4]) 。影响分析(即探查对估计或预测有异常大影响的数据)是回归诊断的重要内容，尽管可以使用很多种统计量来进行影响分析，但我们常常采用Cook统计量进行度量(参见文献[5-8])。本文仍采用Cook统计量对约束线性回归模型进行影响分析。

1 刀切约束最小二乘估计

用Y(i),X(i),e(i)分别表示从Y,X,e剔除第i行所得的向量或矩阵。从线性回归模型(1)剔除第i组数据后，剩余的n-1组数据的线性回归模型为

Y(i)=X(i)β+e(i),Ee(i)=0,Cov(e(i))=σ2In-1

(3)

我们知道，模型(1)在约束条件(2)下的最小二乘估计为

(4)

下面用Lagrange乘子法可以求模型(3)满足线性约束(2)的最小二乘估计。记

(5)

则线性约束(2)可以改写为

(6)

问题转化为在(6)的k个条件下，求β使Q(β)=‖y(i)-X(i)β‖2达到最小值。为此构造辅助函数

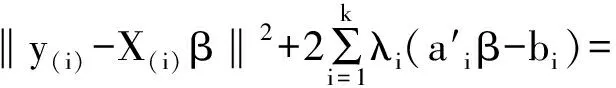
‖y(i)-X(i)β‖2+2λ′(Aβ-b)=

(y(i)-X(i)β)′(y(i)-X(i)β)+2λ′(Aβ-b)

其中λ=(λ1,…,λk)′为Langrange乘子。对函数F(β,λ)求对β0,β1,…,βp-1的偏导数,整理并令它们等于零,得到

(7)

联立(7)式和线性约束(2)式，得到λ的估计和约束最小二乘估计分别为

(8)

(9)

2 Cook统计量

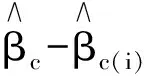
(10)

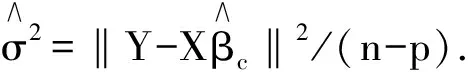
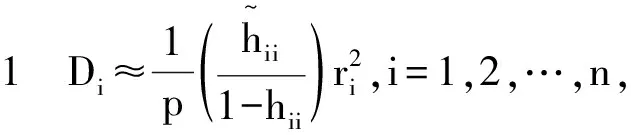
证明 注意到(参见文献[9])

(11)

可以得到

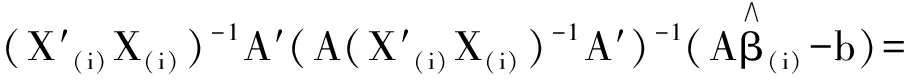
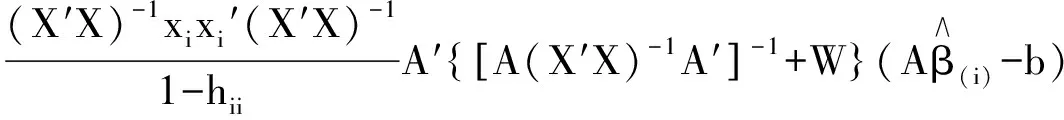
(12)

其中

由(4)(9)(12)式得

(13)

其中

(14)

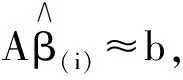
(15)

又容易得到(参见文献[9])

(16)

由(10)(15)(16)式即可得到定理1.至此定理证明完毕。

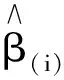
注2．定理1在形式上与基于其它估计的Cook距离相同(如：文献[9]基于最小二乘估计，文献[10]基于稳健估计等)，因而在一定程度上说明了我们的结论是合理的。

注3． 定理1是采用Cook距离进行数据的影响分析，还可以用其它距离，如：Welsch-Kuh距离、Hadi测度、Pena距离、似然距离等[10～12]等)。

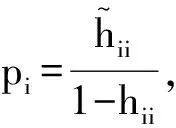
3 应用

某科学基金会的管理人员欲了解从事研究工作的中、高水平的数学家的年工资额Y与他们的研究成果的质量指标X1、从事研究工作的时间X2以及能成功获得资助的指标X3之间的关系。为此按一定的设计方案调查了24位数学家，得到数据如表1所示。

经计算和检验，我们可以得到如下合理的回归方程为

另外，通过检验可以认为X1与X3的系数相等，因此我们可以将本例改为：求在条件β1=β3下的回归方程。此时得到如下回归方程：

经计算，精确和近似Cook距离均表明没有强影响数据。为了说明我们方法的有效性，将19号数学家的年工资额从38.0改为138.0，得到精确Cook距离为D19=1.05564和近似Cook距离为D19≈1.05045,二者相差较小，均远远大于其它点，二者均说明19号数据是强影响点，进而说明本文方法的有效性。

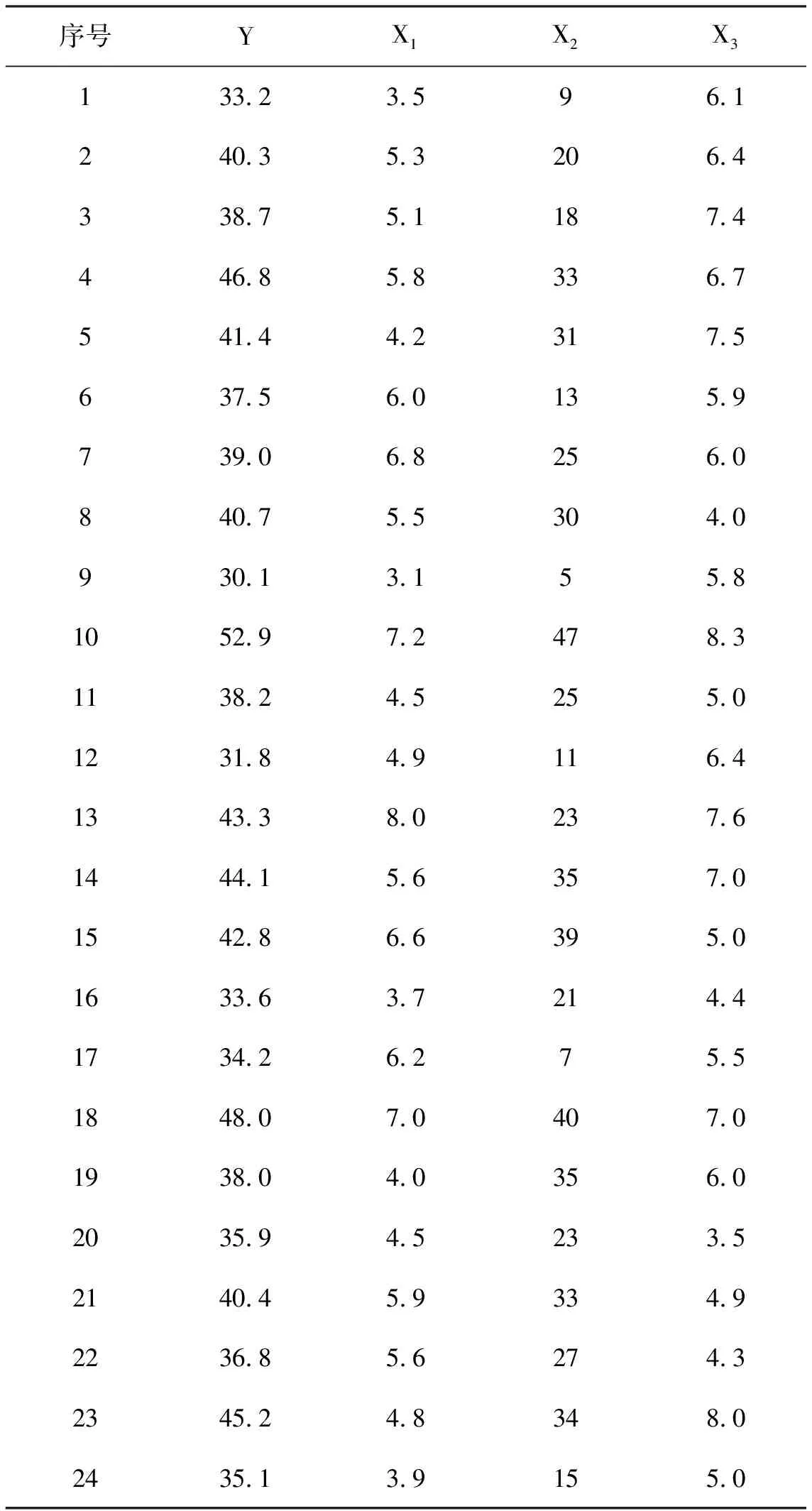
表1 24位数学家的数据

参考文献：

[1]Guil GR, Engela B, Norberto C, et al.Least squares estimation of linear regression models for convex compact random sets[J].Advances in Data Analysis and Classification，2007, 1: 67～81.

[2]Hampel F R, Ronchetti E M, Rousseeuw P J, et al.Robust Statistics[M].New York:John Wiley & Sons, 1986.

[3]Li Y, Yang H.A new stochastic mixed ridge estimator in linear regression model[J].Statistical papers,2010, 51(2):315～323.

[4]Sakallioglu S, Kaciranlar S.A new biased esimator based on ridge estimation[J].Statistical Papers, 2008, 49: 669～689.

[5]Cook R D.Detection of influential observations in linear regression[J].Technometrics, 1977, 19:15～18.

[6]Vens M, Ziegler A.Generalized estimating equations and regression diagnostics for longitudinal controlled clinical trials: A case study[J].Computational Statistics and Data Analysis, 2012, 56(5):1232～1242.

[7]Venezuela M K, Sandoval M C, Botter D A.Local influence in estimating equations[J].Computational Statistics and Data Analysis, 2011, 55: 1867～1883.

[8]Diaz-Garcia JA, Gonzalez-Farias G.A note on the Cook's distance[J].Journal of Statistical Planning and Inference, 2004, 120:119～136.

[9]王松桂，陈 敏，陈立萍.线性统计模型：线性回归与方差分析[M].北京：高等教育出版社，1999.

[10]Türkan S, Cetin MC, Toktamis O.Outlier detection by regression diagnostics based on robust parameter estimates[J].Hacettepe Journal of Mathematics and Statistics, 2012,41(1):147～155.

[11]Belsley D A, Kuh E, Welsch R E.Regression Diagnostics: Identifying Influential Data and Sources of Collinearity[M].New York: John Wiley & Sons, 1980.

[12]孟丽丽，卢志义.基于Pena距离的加权最小二乘估计的影响分析[J].数理统计与管理，2009,28(2):252～257.