菌群优化算法研究综述

武林娟，胡桂武，陈建超

(1.广东商学院 经济贸易与统计学院，广东 广州 510320;2.广东商学院 数学与计算科学学院，广东 广州 510320;3.中国人民大学 教育部数据工程与知识工程重点实验室,北京 100872)

0 引言

自从仿生学创立以来，学者们从模仿生物出发，创造了很多含有新功能的计算工具。比如对社会性动物(如蚁群、鸟群、鱼群等)的自组织行为进行数学建模并利用计算机对其进行仿真，这就是群智能(Swarm Intelligence，SI)的起源。群智能做为新兴的优化方法，从整体上来说尚有大量的问题需要解决。

近年来有些学者尝试对微生物的行为机制及其生理特性进行建模仿真，构建了一些新型群智能算法，最优代表性的是菌群觅食优化算法(Bacteria Foraging Optimization，BFO)[1]，从而丰富仿生优化算法中的微生物智能计算这一领域，由于微生物智能仿生技术问世的时间太短，国际学术界目前对BFO等相关研究尚有许多空白，这一新型的群智能优化算法还远未获得学术界应有的足够重视。

1 基本菌群优化算法

菌群优化算法[1]算法的基本思路是从初始化一组随机解开始，将细菌的位置表示为问题的潜在解，通过细菌的趋化操作实现细菌下一步趋向更为有利的生存环境，获得较优的位置；通过复制操作保留优秀个体淘汰较差个体，从而实现整个细菌群体收敛到局部最优；通过迁移操作可以在一定程度上避免算法陷入局部最优。

细菌觅食优化算法对待优化问题进行求解的一般过程设为：对问题进行解的编码；设计问题的评价函数；随机产生初始群体；利用趋化、繁殖和迁移算子进行迭代优化，算法的主要实现步骤描述如下：

步骤1：初始化各参数。其中，Ned为迁移次数、Nre为繁殖次数、Nc为趋化次数；Ped为基本迁移概率；S为细菌规模数；Ns为游动次数。

步骤2：初始化细菌位置。采用式(1)产生初始化位置，利用适应度函数计算细菌的初始化适应度值。

X=xmin+rand*(xmax-xmin)

(1)

其中，rand为均匀分布在[0,1]区间的随机数。

步骤3：迁移循环l=1:Ned；繁殖循环K=1:Nre；趋化循环j=1:Nc，使用θi(j,k,l)表示第i个细菌的空间位置向量，其中j表示第j代趋化循环，k表示第k代繁殖循环，l表示第l代迁移循环。

步骤4：执行细菌趋化循环.

步骤4.1.翻转,按照公式(2)更新细菌位置

(2)

θi(j,k,l) 表示第i个体在第j代趋药性循环,第k代复制循环，第l代迁移循环时的位置， △(i)表示方向调整后选定的方向向量，向量中的元素属于区间[-1，1]，C(i)表示前进的步长。

步骤4.2.游动:如果翻转的适应值改善，则按照翻转的方向进行游动，直至适应值不再改善或达到设定的最大移动步数Ns为止。基于细菌感应机制的适应度采用Jcc表示：

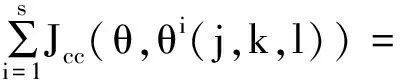
(3)

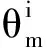
J(Xi)=J(Xi)+Jcc(Xi)

(4)

因此聚集操作就是通过上述公式来对适应值J(Xi)进行修正，使得细菌达到聚集的目的。

步骤5：繁殖循环。趋化周期完成后，对每个细菌在生命周期内的适应度进行累加得到细菌能量，按照细菌能量进行排序，淘汰掉能量获取能力差的半数细菌，对能量获取能力较强的半数细菌进行再生。

步骤6：迁移循环。繁殖算子完成后，生成一个随机概率，并将它与固定迁移概率Ped,如果小于Ped就进行细菌迁移，在解空间内按照公式(1)初始化。

步骤7：循环结束条件判断，满足则结束，输出结果。

3 菌群优化算法的研究状况

3.1 理论研究

该领域最早的理论研究可上溯到1986 Stephens D和Krebs J的著作《Foraging Theory》[2].2000年Passino Kevin M[3]研究了单个细菌的智能，并且应用于分布式优化和控制，对大肠杆菌的趋化行为进行了理论建模和稳定性分析。2002年Passino K M[1]提出了BFO，并且详细分析了其仿生基础，开始受到计算机界的重视。2003年Liu Y和Passino Kevin M[4]对多维菌群模型情况下的稳定性进行了分析和证明。2004年Gazi V和Passino K M[5]对基于菌群吸引与排斥行为的模型进行了稳定性分析。2009年Sambarta Dasgupta[6]等人对BFO的趋化操作进行自适用改进，并且做了严谨的数学理论分析。2009年Sambarta Dasgupta[7]等人对BFO的理论基础、理论分析、应用做了详细的阐述,进行了详细的理论基础以及收敛性分析。2009年Sambarta Dasgupta[8]等人对BFO的趋化动能的稳定性进行了分析。2010 年Arijit Biswas, Swagatam Das[9]等人对BFO的复制操作的稳定性进行了分析。

总体来说菌群优化算法作为一种新型群智能优化算法，数学理论基础薄弱，普遍意义的理论性分析不充分，待更深入的研究。

3.2 算法改进

任何群智能算法不具备绝对的完备性和可信度，菌群优化算法作为一种新的群智能算法，以提高算法性能的理论、算法设计以及与其它算法的融合研究是群智能研究的必经之路[10～11]。在参数调整方面，2003年Liu Y等改进了大肠杆菌间的相互作用机制，并对收敛性进行了初步分析[2]；2005年Mishra等基于TS的模糊规则系统提出了改进MBFO算法[12]；2006年Tripathy和Mishra等改进了适应度函数，提出了改进型的BFOA[13]，2008年Datta设计了一种具有自适应趋化步长的BFO算法[14]；2009年Majhi等设计了自动趋化步长的BFO模型，并将其应用于神经网络的训练[15]。

2010年Niu 等[16]在BFO算法中引入趋化步长的线性变化和非线性变化，并且应用到投资组合优化问题。此外，2011年Biswas 等[17]基于BFO算法中繁殖操作的简单数学分析，提出了一个新的算法，表现优于标准BFO算法。

以上算法的研究主要是针对趋化的改进，对复制、迁徙等方面的研究比较少，对算法模式的泛化设计鲜见。

3.3 算法混合研究

菌群优化算法的另外一个研究方向是将BFO与其它优化方法相结合,克服单个算法的不足，成为克服群智能算法缺点的一个十分有效的工具[13]。

Kim等[18]提出了一个新的基于模糊方法、觅食行为和克隆选择的混合模型。Biswas等将BFO算法与粒子群算法相结合，提出了一种混合优化算法并应用于多峰函数优化[19]。

Kim等人在BFO算法中引入了遗传算法的交叉、变异算子，提出了GABFO算法[20]，并用于函数优化问题；Dasgupta等人[21]将差分进化(DE)的变异与交叉引入BFO算法，提出了趋向性差分进化(CDE)，提高了BFO算法在处理高维问题时的性能。

Panigrahi等人[22]把单纯形法和细菌觅食行为相结合，提出一种新的随机混合优化方法。Chu等[23]结合BFO算法中大肠杆菌的觅食机制和PSO算法中鸟群的集群模式提出了快速细菌群算法(FBSA)。

Lohokare等[24]基于BBO算法和BFO算法的混合提出了智能生物地理学优化(IBBO)方法，结果比BBO算法和其它修正算法更优。Shao等[25]把BFO算法与禁忌搜索混合，得到TS-BFO混合算法，对于模式发现来说是一个具有潜力的方法。

Hanmandlu等[26]使用模糊逻辑技术扩展了BFO算法，涉及迭代学习的BFO算法比GA和熵方法有更好的表现。

通过以上的研究可以看到，BFO算法和群体智能、进化计算、混沌优化等的混合研究还有很大的研究空间。

3.4 应用研究

随着菌群优化算法研究的不断发展,研究者已尝试着将其用于工程、控制领域、经济等相关领域,并取得了较好的成果[13]。

Tripathy和Mishra将BFOA用于优化mesh电力网络的有效功率损耗问题[11]、Kim利用BFO来优化神经网络的权重[27]。

Farhat等[28]用线性递减的趋化步长取代原始BFO算法中不变的趋化步长，求解STHTS问题。

Datta等[17]将自适应增量调制引入BFO算法中，用以优化直线天线阵权重的振幅和相位，提高了收敛速度和精度。

Majhi等[19]使用BFO和自适应BFO技术发展了有效预测模型用于各种股票指数的预测。

Kulkarni等[29]在无线传感器网络的分布式迭代定位问题中使用BFO算法，从定位节点数量、定位信息的精确度和计算时间三方面对BFO和PSO进行了比较。

Majhi等[30]在自适应信道均衡器中使用BFO算法适当地更新均衡器的权重。新的均衡器改进了收敛性和误码率。

通过以上的研究可以看到，BFO算法在连续优化问题中取得了很好的成果，PID控制器的设计等工程、控制领域的应用取得了一些成功，再金融等经济领域也有一些尝试，但由于是新的算法，其应用研究特别在离散领域的研究有待进一步加强。

4 总结和展望

菌群优化算法作为一种新兴的群智能技术，凭借着其算法结构简单、灵活、鲁棒性强和自组织能力等优点吸引了学者越来越多的关注，为人工智能处理系统和算法的设计提供了有益的启发。但是,菌群优化算法是一种新兴的群智能算法，还存在诸多需要完善的地方，存在的问题及其未来研究方向主要有以下几方面：

1)菌群优化算法缺乏具备普遍意义的理论性分析，数学理论基础薄弱。算法参数比较多，对各种参数设置没有确切的理论依据，通常都是按照经验型方法确定,具有很强的不确定性。

2)菌群优化算法模式设计研究不足，聚集操作中函数的通用性设计值得研究，适应值修正操作对适应值函数依赖性比较高，影响算法的稳定性，复制操作操作有一定的主观性，限制了该算法求解诸如：动态优化、多目标优化等复杂优化问题的能力。

3)算法性能评估及其评估标准测试集研究不足，与其它经典算法比较研究不充分，主要研究是停留在连续的优化问题上，基于离散问题的很少涉及。

将来的研究工作,应以更高层次的数学或人工智能理论为基础的菌群优化算法研究，进一步探寻算法的基本原理，夯实理论基础。另外,还应扩展菌群优化算法在工程、控制领域、经济、管理等领域的应用研究，与神经计算、混沌优化、进化计算、移动计算等各种先进技术的融合亟待更深入的研究。

参考文献:

[1]Passino K M.Biomimicry of Bacterial Foraging for Distributed Optimization and Control[J].IEEE Control Systems Magazine, 2002, 22(3): 52～67.

[2]Stephens D W, Krebs J R.Foraging Theory [M].NJ: Princeton University Press,1986.

[3]Passino K M.Distributed Optimization and Control Using Only a Germ of Intelligence[J].IEEE International Symposium on Intelligent Control,2000:5～13.

[4]Liu Y, Passino K M, Polycarpou M.Stability analysis of m-dimensional asynchronous swarms with a fixed communication topology [J].IEEE Trans on Automatic Control, 2003,48(1):76～95.

[5]Gazi V, Passino K M.Stability Analysis of Social Foraging Swarms[J].IEEE Trans on Systems, Man and Cystems PART B: Cybernetic, 2004,34(1):539～557.

[6]Dasgupta S, Biswas A, Abraham A.Adaptive Computational Chemotaxis in Bacterial Foraging Optimization: An Analysis[J].IEEE Transactions on Evolutionary Computation, 2009,13(4): 919～941.

[7]Das S, Biswas A, Dasgupta S.Bacterial Foraging Optimization Algorithm: Theoretical Foundations, Analysis, and Application[J].Foundations of Computational Intelligence, 2009,3: 23～55.

[8]Dasgupta S, Das S, Abraham A, et al.On Stability of the Chemotactic Dynamics in Bacterial-Foraging Optimization Algorithm[J].IEEE Transactions on systems, man, and cybernetics, 2009,39(3):670～679.

[9]Biswas A, Das S, Abraham A, et al.Stability analysis of the reproduction operator in bacterial foraging optimization [J].Theoretical Computer Science,2010:2127～2139.

[10]Ben Niu, Yan Fan, Lijing Tan, et al.A Review of Bacterial Foraging Optimization Part I: Background and Development[J].Advanced Intelligent Computing Theories and Applications Communications in Computer and Information Science, 2010(93):535-543.

[11]Ben Niu, Yan Fan, Lijing Tan,et al.A Review of Bacterial Foraging Optimization Part II: Background and Development[J].Advanced Intelligent Computing Theories and Applications Communications in Computer and Information Science, 2010(93):544～550.

[12]Mishra S.A hybrid least square-fuzzy bacterial foraging strategy for harmonic estimation[J].IEEE Transactions on Evolutionary Computation,2005,9(1): 61～73.

[13]Tripathy M, Mishra S.Bacteria foraging-based to optimize both real power loss and voltage stability limit[J].IEEE Transactions on Power systems ,2007,22(1):240～248.

[14]Datta T, Misra I S, Mangaraj B B, et al.Improved adaptive bacteria foraging algorithm in optimization of antenna array for faster convergence[J].Progress in Electromagnetics Research C,2008,1: 143～157.

[15]Majhi R, Panda G, Sahoo G.Efficient Prediction of Stock Market Indices Using Adaptive Bacterial Foraging Optimization (ABFO) and BFO Based Techniques[J].Expert Systems with Applications,2009,36(6):10097～10104.

[16]Niu B, Fan Y, Zhao P, et al.A Novel Bacterial Foraging Optimizer with Linear Decreasing Chemotaxis Step[C].Proceedings of 2nd International Workshop on Intelligent Systems and Applications, Wuhan, China, 2010:1～4.

[17]Abraham A, Biswas A, Dasgupta S, et al.Analysis of the Reproduction Operator in an Artificial Bacterial Foraging System[J].Applied Mathematics and Computation,2010,215(9): 3343～3355.

[18]Kim D H, Cho J H.Advanced Bacterial Foraging and Its Application Using Fuzzy Logic Based Variable Step Size and Clonal Selection of Immune Algorithm[C].International Conference on Hybrid Information Technology, 2006,(1): 293～298.

[19]Biswas A, Dasgupta S, Das S, et al.Synergy of PSO and bacterial foraging optimization-a comparative study on numerical benchmarks[J].Innovatious in Hybrid Intelligent Systems,2007,44:255～263.

[20]Kim D H, Abraham A, Cho J H.A hybrid genetic algorithm and bacterial foraging approach[J].Information Sciences, 2007(177): 3918～3937.

[21]Dasgupta A, Dasgupta S, Das S, et al.A Synergy of Differential Evolution and Bacterial Foraging Optimization for Global Optimization[J].Neural Network Word, 2007,17(6): 607～607.

[22]Paniarahi B K, Ravikumar P V.Bacterial Foraging Optimization: Nelder-Mead Hybrid Algorithm for Economic Load Dispatch[J].IET Generation, Transmission & Distribution, 2008,2(4):556～565.

[23]Chu Y, Mi H, Liao H, et al.A Fast Bacterial Swarming Algorithm for High-Dimensional Function Optimization[C].IEEE World Congress on Computational Intelligence, 2008: 3135～3140.

[24]Lohokare M R, Pattnaik S S, Devi S, et al.Intelligent Biogeography-Based Optimization for Discrete Variables[J].World Congress on Nature & Biologically Inspired Computing, 2009:1088～1093.

[25]Shao L, Chen Y.Bacterial Foraging Optimization Algorithm Integrating Tabu Search for Motif Discovery[J].IEEE International Conference on Bioinformatics and Biomedicine, 2009:415～418.

[26]Hanmandlu M, Verma O P, Kumar N K, et al.A Novel Optimal Fuzzy System for Color Image Enhancement Using Bacterial Foraging[J].IEEE Transactions on Instrumentation and Measurement,2009,58(8): 2867～2879.

[27]Kim D H, Cho C H.Bacterial foraging based neural network fuzzy learning[C].IICAI 2005,2005:2030～2036.

[28]Farhat I A, El-Hawary M E.Short-Term Hydro-Thermal Scheduling Using an Improved Bacterial Foraging Algorithm [J].IEEE Conference on Electrical Power & Energy, 2009: 1～5.

[29]Kulkarni R V, Venayagamoorthy G K, Cheng M X.Bio-Inspired Node Localization in Wireless Sensor Networks[J].IEEE International Conference on Systems, Man and Cybernetics, 2009: 205～210.

[30]Majhi B, Panda G, Choubey A.On the Development of a New Adaptive Channel Equalizer Using Bacterial Foraging Optimization Technique[J].IEEE Annual India Conference, 2006:1～6.