有限域上线性q-相伴多项式及其应用

陈引兰

(湖北师范学院 数学与统计学院,湖北 黄石 435002)

1 由q-相伴多项式构造高次不可约多项式或本原多项式

有限域上的不可约多项式作为有限域上多项式环的素元，在构造有限域和计算有限域中的元素时都是必不可少的，而且在密码、编码理论及随机数的产生等方面也有着广泛的应用[1～3]。

关于有限域Fq上不可约多项式的存在性问题，设n是给定的正整数，d|n，记Nq(n) 为Fq上所有n次首1不可约多项式的个数，μ(d) 表示莫比乌斯函数。我们有：

由此可知，有限域Fq上n次不可约多项式存在，而且随n增大而增加，但要构造出任意次数的所有不可约多项式仍然是困难的。本节利用线性q-相伴多项式由低次不可约或本原多项式构造高次不可约多项式或本原多项式。为此，先介绍线性q- 相伴多项式。

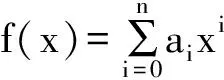
定理1[2]设f(x)是Fq[x] 上不可约多项式，F(x)为f(x) 的线性q-相伴多项式，记g(x)=F(x)/x，则g(x)的任一不可约因式的次数均为ord(f(x)) .

注 在Fq[x] 中，使得f(x)|(xn-1) 的最小的正整数n称为f(x)的阶，记为ord(f(x)) .

本原多项式一定是不可约多项式，但不可约多项式不一定是本原多项式。Fq上n次本原多项式是Fq上所有n次不可约多项式中阶最高(qn-1) 的多项式。下面的结论推广了文[3]中的结论(定理3)。

定理2 设f(x) 是Fq[x] 上不可约多项式，且f(0)≠0，则g(x)=F(x)/x在Fq[x] 上不可约的充分必要条件是f(x) 是Fq[x] 上的本原多项式或本原多项式的非零常数倍。

证明 充分性:设f(x) 是Fq[x]上的本原多项式或本原多项式的非零常数倍，且deg(f(x))=n，则f(x)为Fq[x]上的不可约多项式，且ord(f(x))=qn-1.由定理1知：g(x)的任一不可约因式的次数均为ord(f(x))=qn-1，而deg(g(x))=qn-1，所以g(x) 为Fq[x] 上的不可约多项式。

必要性:设g(x)=F(x)/x在Fq[x] 上不可约，又f(x)是Fq[x]上不可约多项式，且f(0)≠0，由定理1知： deg(g(x))=ord(f(x)),而deg(g(x))=qn-1，所以ord(f(x))=qn-1，即：f(x) 为Fq[x] 上n次qn-1 阶且f(0)≠0的不可约多项式。

若f(x)是首1的，则f(x)是Fq[x]上的本原多项式；

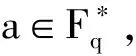
定理得证。

对于定理2，何时g(x) 仍为Fq[x]上的本原多项式呢？当f(x)是Fq[x]上的本原多项式或本原多项式的非零常数倍时，将g(x)看作定理中的f(x) ，不难得到:

定理3g*(x)=G(x)/x在Fq[x] 上不可约的充分必要条件是g(x)=F(x)/x为Fq[x] 上的本原多项式。其中G(x)是g(x)的线性q-相伴多项式。

特别地，若f(x) 是F2[x] 上的n次本原多项式，且f(0)≠0，则g(x)=F(x)/x为F2[x]上的 2n-1次不可约多项式，当 22n-1-1为素数时，2n-1 一定为素数(见文[4])，此时有ord(g(x))|(22n-1-1)，而22n-1-1 为素数，且ord(g(x))>1，所以ord(g(x))=22n-1-1，即g(x)为Fq[x] 上的本原多项式，故g*(x)=G(x)/x在Fq[x]上不可约。于是有

推论1 当 22n-1-1为素数时，若f(x) 是F2[x] 上的本原n次多项式，则g(x) 为F2[x] 上2n-1 次本原多项式。

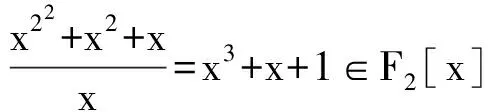
2 由 q-相伴多项式求两高次多项式的最大公因式

先证明多项式与其q-相伴多项式的整除关系等价。文[2]中下面的结论是借助形式除法的定义给出证明的。这里我们直接证明该结论。

定理4 设L1(x),L2(x) 分别是Fq[x]上多项式l1(x),l2(x)的线性q-相伴多项式，则下列条件等价：

1)L1(x)|L2(x);

2)l1(x)|l2(x).

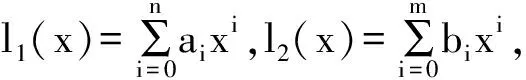
若L1(x)|L2(x),设l2(x)=l1(x)·h(x)+r(x) ，其中0≤deg(r(x))

反之，若l1(x)|l2(x) ，设l2(x)=g(x)·l1(x) ,则L2(x)=G(L1(x))，其中G(x)是多项式g(x)的线性q-相伴多项式，于是L1(x)|L2(x).

由定理4，我们容易得到下面求最大公因式的定理。

定理5 设L1(x),L2(x) 分别是Fq[x]上多项式l1(x),l2(x)的线性q-相伴多项式，且 (l1(x)，l2(x))=h(x),则(L1(x),L2(x))=H(x)，其中H(x)是多项式h(x)的线性q-相伴多项式。

由定理5知，要求某些高次多项式的最大公因式，而他们是某些多项式的线性q-相伴多项式，从而转化为求次数低的原多项式的最大公因式，比直接求大大减少了计算量。

例2 求多项式L1(x)=x64+x16+x8+x4+x2+x∈F2[x],L2(x)=x32+x8+x2+x∈F2[x] 的最大公因式。

解 在F2[x]上，与L1(x),L2(x)线性q-相伴多项式分别是l1(x)=x6+x4+x3+x2+x+1,l2(x)=x5+x3+x+1,由辗转相除法，得(l1(x),l2(x))=x+1. 于是,(L1(x),L2(x))=x2+x.

参考文献:

[1]万哲先.代数和编码[M].北京:高等教育出版社，2007.

[2]Lidl R,Niedrreiter H.Finite Fields[M]． Cambridge:Cambridge Univ Press, 1997.

[3]郭宝安，蔡长年.有限域上的不可约多项式[J].北京邮电大学学报,1994,1(17):23～26.

[4]闵嗣鹤，严士健.初等数论(第三版)[M]．北京:高等教育出版社，2005.