缺失数据p-范分布的极大似然估计
伍 丽,卢冬晖,李邦荣(湖北师范学院 数学与统计学院,湖北 黄石 435002)
0 引言
文献[1]根据偶然误差的基本统计特性推导了偶然误差的一般分布密度函数——p范分布.对于一元的情形,该分布由μ,σ和p三个参数确定。常用的退化分布、拉普拉斯分布、正态分布和均匀分布都是这一分布的特列(分别对应于p→0,p=1,p=2和p→+∞).这些分布在生产实践中有着大量的应用,对于其优良性质都有大量研究.在缺失数据类型中有一种非常重要的形式,即为每次观测时观测值以一定的概率被观测到,对于部分缺失数据指数分布、 poisson分布、几何分布总体的统计推断问题在一些文献中已经进行了较深入地讨论[2~4].但对于p-范分布在缺失数据情况下的研究较少,本文利用具有部分缺失数据的总体统计推断方法[5],得到一元p-范分布的未知参数σ的极大似然估计,并证明了此参数极大似然估计具有强相合性和渐近正态性。
1 极大似然估计
定义1 均值为零(否则以ξ-Eξ代替ξ)的随机变量ξ的密度函数为
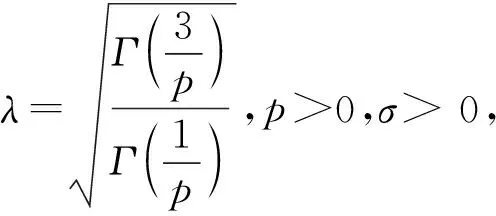
下面在p已知的条件,用极大似然法估计未知参数σ,为此先介绍如下性质.
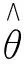
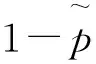
取对数得
对σ求偏导,并令之为0,得
有此得σp的极大似然估计为
从而由性质1得
2 极大似然估计量的渐近性质
为了证明以下结论,我们首先介绍3个引理.
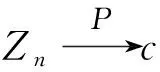
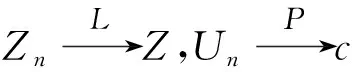
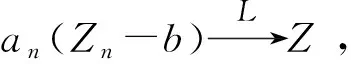
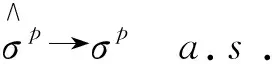
证明 由强大数定律可知:
(1)
(2)
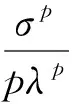
又有
由引理1有
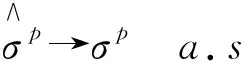
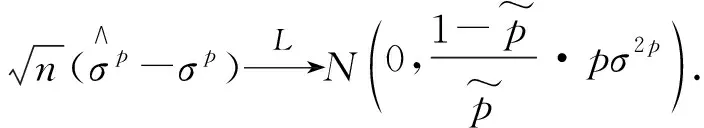
证明 因为
则有
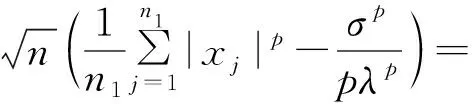
I1+I2
(3)

(4)
由(2)(4)或引理2知
I1→0a.s
(5)
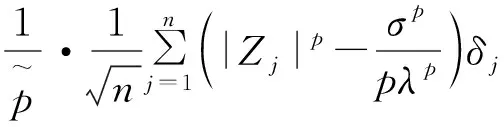
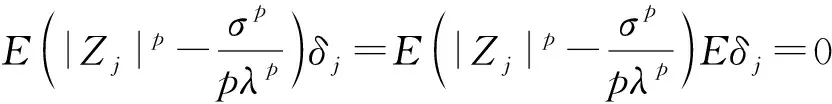
由中心极限定理有
(6)
由(3)(5)(6)及引理2有
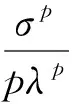
由引理3有

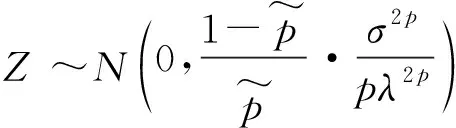
即
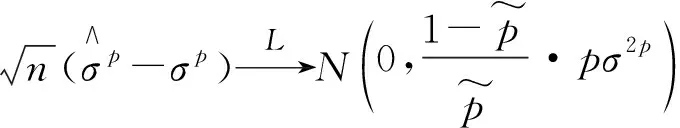
证毕.
注:本文仅对特殊的只含一个未知参数的一元p-范分布在缺失数据情况下,利用所观测到的数据对总体参数进行了极大似然估计,并证明了它的强相合性和渐近正态性。但对于一般情况还有待进一步研究。
参考文献:
[1]孙海燕.误差分析的一般形式[J].武汉测绘科技大学学报,1993,18(3):49~56.
[2]Koskinen J H, Robins G L, Pattison P E.Analysing exponential random graph (p-star) models with missing data using Bayesian data augmentation[J].Statistical Methodology,2010,7(3): 366~384.
[3]Yang Y, Kang J.Joint analysis of mixed Poisson and continuous longitudinal data with nonignorable missing values[J].Computational Statistics & Data Analysis,2010,54(1):193~207.
[4]Yu Shun-zheng, Kobayashi H.A hidden semi-Markov model with missing data and multiple observation sequences for mobility tracking[J].Signal Processing,2003,83(2):235~250.
[5]Gupta R D, Kundu D.A new class of weighted exponential distributions[J].Statistics-A Journal of Theoretical and Applied Statistics,2009,43(6):621~634.
[6]孙海燕,胡宏昌. p-范分布及其抽样分布[J].应用概率统计,2003,19(4):424~428.
[7]Serfling R J.Apprvximatim Theorems of Mathematical Statistics[M].New York:John Wiley&Sons,1980.
[8]茆诗松,王静龙,濮晓龙.高等数理统计(第二版)[M].北京:高等教育出版社,2006.

