栅格型分布式流域水文模型构建
关传弢,李 丹,王贵作
(1.中水东北勘测设计研究有限责任公司,长春130021;2.水利部松辽水利委员会,长春130021;3.水利部发展研究中心,北京100038)
流域水文模型是管理水资源和生态环境的重要工具。水文学家更加重视到下垫面因子空间分布的不均匀性对流域降雨径流的形成有着至关重要的影响。Linsley和Crawford[1]及赵人俊等运用统计学方法开展相关研究的。虽然考虑到下垫面因子空间分布不均匀,但只能用于模拟气候和下垫面因子空间分布均匀的虚拟状态,只能给出空间均化的模拟结果,不能确定地给出流域下垫面因子真实的空间分布,而分布式水文模型能够客观地反映出气候和下垫面因子的空间分布对流域降雨径流形成的影响。分布式需要大量的流域空间分布数据信息和相关技术的支持,传统地面观测站网的密度远不能满足模型对数据的要求,遥感影像可以获得大量的流域空间信息,GIS技术是将遥感信息转变成水文模型所需数据的重要工具[2]。栅格式的遥感影像与分布式水文模型的输入数据格式具有一致性,给模型概念理解和使用上都带来了方便。在前人研究基础上,以遥感和GIS技术作支撑开展基于空间变化的栅格水文模型研究,构建一种考虑流域下垫面空间变异性的新型水文模型。本模型不但适用于南方湿润地区,在北方寒冷和干旱半干旱地区也可以获得较为理想的模拟效果。
1 蓄水容量空间分布模块
新安江模型和TOPMODEL提出了蓄水容量分布曲线和流域蓄水容量,在此基础上,依据植被根系层深度的空间变化规律,结合各类型土壤的水分参数,描述流域蓄水容量的空间分布。提出栅格张力水蓄水容量、栅格自由水蓄水容量概念,以栅格植被根系层深度、田间持水量计算流域内各点栅格张力水蓄水容量,这里假设栅格自由水蓄水容量为栅格张力水蓄水容量的函数[3]。
1.1 栅格张力水蓄水容量
这里定义为栅格植被根系层深度与栅格田间持水量的乘积,见式(1):

式中:Sc为栅格张力水蓄水容量,mm;φ为栅格田间持水量,mm;Zr为栅格植被根系层深度,mm。
不同坡度坡地的植被根系层深度模型见式(2):

式中:Zr为植被根系层深度,mm;θ为坡地坡度,(°);θ1为上临界坡度,(°);θ2为下临界坡度,(°);Z为特征植被根系深度,mm。
临界土层深度是特征根系深度的函数,见式(3):

式中:L1为临界土层深度,mm;κ为临界土层深度参数。
1.2 栅格自由水蓄水容量
栅格自由水蓄水容量受土壤类型和植被根系层深度影响,见式(4)。

式中:S为栅格自由水蓄水容量,mm;β为参数。
2 垂直混合产流模块
基于蓄水容量空间分布模型,结合垂向混合产流机制提出栅格化蓄水容量的垂向混合产流模型。在该模型中,首先采用简化的Green—Ampt公式[4]将净雨划分出地表径流,其余水量进入土壤,满足土壤张力水蓄水容量后成为径流R(mm)。当径流量大于自由水蓄水容量时,多出水量也将会出露地表,成为地表径流,同时产生壤中流和地下径流;当径流量小于自由水蓄水容量时,仅产生壤中流和地下径流。壤中流和地下径流通过壤中流出流系数和地下径流出流系数划分壤中自由水蓄量得到。
2.1 地表径流
采用简化的Green-Ampt公式划分地表径流,当净雨量大于实际下渗量时,有地表径流产生:

式中:FM为渗漏能力,mm;FC为稳定入渗率mm;FK为土壤缺水量对下渗率影响的灵敏系数;FA为实际下渗量,mm;So实际土壤含水量,mm;RS为地表径流,mm。
当径流量大于自由水蓄水容量时,多出水量也将会出露地表,成为地表径流,此时自由水蓄量SS等于栅格自由水蓄水容量:
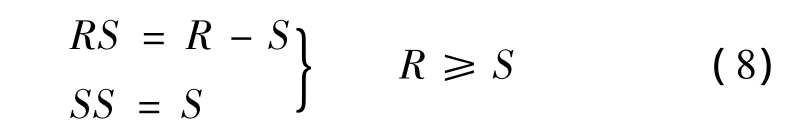
2.2 壤中流和地下径流
当径流量小于自由水蓄水容量时,仅产生壤中流和地下径流,自由水蓄量等于径流量:

壤中流和地下径流通过壤中流出流系数KI和地下径流出流系数KG划分,计算如下:

式中:RI为壤中流,mm;RG为地下径流,mm;KI为壤中流出流系数;KG为地下径流出流系数。
3 积雪融雪模块
本文构建的模型中积雪融雪模块分积雪、融雪、融水出流和融水冻结4个过程。采用“度日因子法”[5]模拟积雪融雪过程。虽然“能量平衡法”能够很好的描述积雪融雪过程,但其建立的模型复杂且求解能量平衡方程所需的参数及数据不易获取,本文构建模型时未采用。
3.1 积雪过程
降水量包括降雨量和降雪量,地表空气温度决定了降水是以降雨或是降雪形式到达地表。目前有多种区分雨雪的计算方法,本模型采用的是计算简便且需求数据较少的利用地表空气温度划分雨雪的方法。地表空气温度划分雨雪的方法示意见图1。

式中:Ta为近地表温度,℃;Pr为降雨量,mm;Ps为降雪量,mm;P为降水量,mm;Tr为温度阈值,当地表温度高于等于Tr时,降水以降雨的形式到达地表;Tb为温度阈值,当地表温度≥Tb时,降水以降雪的形式到达地表。
温度阈值Tr和Tb的取值因气候区不同而不同,本模型取用美国国家气象服务中心(National Weather Service,2005)推荐数值,Tr取值为2℃,Tb取值为0℃。
3.2 融雪过程
融雪受控于积雪表面的能量平衡,但提供大量的时间空间数据用以能量平衡计算是十分困难的,因此本模型采用简洁的度日模型[6],见式(16)。
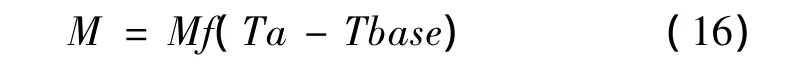
式中:M为融雪速率(mm day-1);Mf为度日因子(mm℃-1day-1);Tbase是温度阈值(℃),当气温高于Tbase时,将发生积雪融化;Mf取值范围(1 mm day-1<Mf<8 mm day-1)(Gray and Male 1981,U.S.Army Corps of Engineers 1956),取值因地区不同而不同(DeWalle et al.,2002)。
3.3 融水出流
当液态水量超过雪块的持蓄容量时将形成融水出流。融水出流估算[6],见式(17):
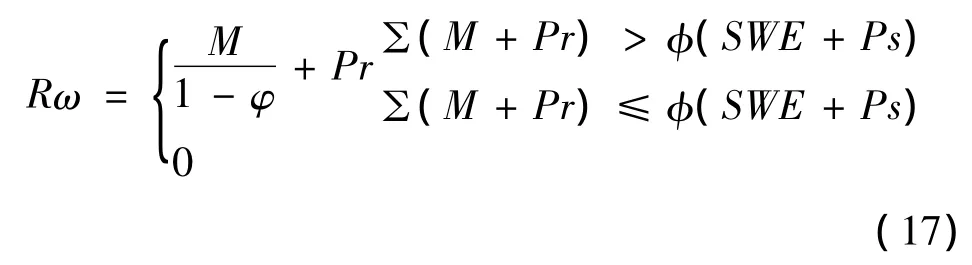
式中:φ为雪块最大融水容量的特征参数;SWE为融雪量,mm。
3.4 融水冻结
当温度下降并低于Tbase时,融水会再次冻结。本模型采用HBV(Bengtssom,1992)模型提供的再冻结计算方法,见式(18):
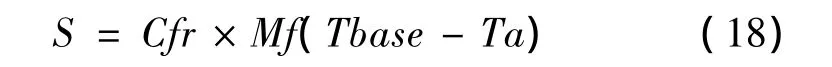
式中:S为再冻结速率(mm day-1);Cfr为再冻结系数。
4 汇流模块
本文构建的模型中汇流模块分别考虑流域水体总入流和河道汇流两个过程,前者包括地表径流、壤中流和地下径流。地表径流因直接汇入邻近下游河道,其汇流量不需另行计算;壤中流和地下径流的汇流量计算分别采用线性水库汇流方法;河道汇流的汇流量计算采用分段马斯京根法。
4.1 流域水体总入流
汇流模块中把经过水源划分得到的地面径流直接汇入流域水体,成为地面径流对流域水体的总入流(TRS);壤中流(RI)流入壤中流蓄水库,经过壤中流蓄水库的消退(壤中流水库的消退系数为CI)过程,成为壤中流对流域水体总入流(TRI);地下径流(RG)进入地下水蓄水库,经过地下水蓄水库的消退(地下水蓄水库的消退系数为CG)过程,成为地下水对流域水体的总入流(TRG)。流域水体总入流的计算如下:

式中:U为单位转换系数,该系数可将径流深,mm,转化为径流量,m3/s;U=F/(3.6×△t)(F为流域面积;△t为单位时段长),TR为流域水体总入流,m3/s。
4.2 河道汇流
河道汇流计算采用马斯京根(MUSKINGUM)分段演算法。为了保证上、下段面的流量在计算时段内呈线性变化和在任何时刻流量在河段内呈线性变化,同时避免出现负出流的不合理现象,一般要求满足约束条件△t≈K。将河段划分成N个子河段后,每个子河段有两个参数 KL、xL。根据水量平衡方程[7]:

式(23)中,I1、I2表示时段始、末的河段入流量;O1、O2表示时段始、末的河段出流量;W1、W2表示时段始、末的槽蓄量;Δt为计算时间步长,h;式(24)中,W为槽蓄量;K为蓄量常数,具有时间因次;x为流量比重因子;I为入流量;O为出流量;式(25)中I1、I2表示时段始、末的子河段入流量;O1、O2表示时段始、末的子河段出流量;式(26)中,KL、xL分别表示长为L的子河段的马斯京根演算参数。
5 结语
本文基于地貌形成理论,充分考虑了植被类型、植被根系深度和土壤类型的空间变化以及土壤水分参数,提出了蓄水容量空间分布模型及建模方法;在此基础上,采用垂直混合产流机制建立了基于蓄水容量空间分布模型的流域水文模型。蓄水容空间分布模型较为合理地描述了研究区域的蓄水容量的空间分布,做到了比分布式概率湿度模型更易于进行流域响应分布的预测。该概念性流域水文模型物理意义较为明确,较合理地揭示了研究区域的产汇流规律,避免了具有物理基础模型的诸多问题,结构简单且能够应用多源数据,适用于流域水文过程模拟及水资源管理、防汛、抗旱等相关领域的应用。本研究也表明建立基于RS和GIS的耦合水文模型是未来的发展趋势。
[1]Linsley K,Crawford N H.Computation of synthetic streamflow record on a digital computer[J].Int Assoc Sci Hydrol Pub,1960(51):526-538.
[2]郑长统,梁虹.分布式水文模型研究进展[J].水科学与工程技术,2009,(6):10.
[3]王贵作.半干旱区分布式水文模型构建与应用研究[D].南京:河海大学,2009.
[4]包为民.垂向混合产流模型及应用[J].水文,1997(3):26-48.
[5]Ao T.,Ishidaira H.,Takeuchi K.,Kiem A.S.,Yoshitari J.,Fukami K.and Magome J.Relating BTOPMCmodel parameters to physical features of MOPEX basins[J].2006(320):84-102.
[6]M.C.Zhou,H.Ishidaira,H.P.Hapuarachchi,J.Magome,A.S.Kiem,K.Takeuchi.Estimating potential evapotranspiration using Shuttleworth–Wallace model and NOAAAVHRR NDVI data to feed a distributed hydrological model over the Mekong River basin [J].Journal of Hydrology,2006(327):151-173.
[7]赵人俊.流域水文模拟—新安江模型与陕北模型[M].北京:水利电力出版社,1984.

