离子色谱法测定水中硫酸根的不确定度分析

孔瑾

（辽宁锦州市环境监测中心站，辽宁 锦州121000）

1 引言

随着生产力的发展和科学技术的进步，人们对测量数据的准确性和可靠性提出了更高的要求，因此，不确定度问题在测量工作中越来越受到重视。不确定度实际上就是指测量结果的可疑程度，是各种不确定度（如标准不确定度、合成标准不确定度、扩展不确定度、A类不确定度、B类不确定度等）的一个总称［1］。本文通过实例，阐述用离子色谱法测定水中硫酸根的不确定度的评定方法。

2 方法原理

样品经预处理后须经0.45μm的微孔滤膜过滤，然后经自动进样器由淋洗液推入分析柱，水样流经离子交换树脂，基于待测阴离子对阴离子树脂的相对亲和力不同而彼此分开，用电导检测器测量相应的阴离子［2］。水样中的阴离子通过色谱峰的保留时间来定性，代入标准曲线用峰高或峰面积来定量。

数学模型为：C＝（h-h0-a）／b。

式中C为待测的浓度，mg／L；h为待测的峰面积；h0为空白峰面积；a为曲线截距；b为曲线斜率。

3 不确定度有关量值

对未知样品进行6次重复性测量，结果分别为：5.76、6.07、5.81、5.96、6.00、5.92mg／L，算术平均值为5.92mg／L（表1）。

表1 水中SO2-4 不确定度有关量值

4 各量值不确定度的计算

4.1 A类不确定度计算

对未知样品进行6次重复测量，通过贝塞尔公式计算出实验标准差：8，平均值标准不确定度：0.047 7；相对标准不确定度：uA＝0.0477／5.92＝0.008 1。

4.2 B类不确定度估算

4.2.1 标准曲线不确定度u1

分别对浓度为1.0、2.0、4.0、6.0、8.0、10mg／L的6个标准溶液测定，峰面积为0.146 9、0.294 0、0.587 4、0.901 6、1.175 0、1.450 0，用最小二乘法求得回归方程y＝0.146x＋0.0066 2，相关系数r＝0.999 7，根据公式：

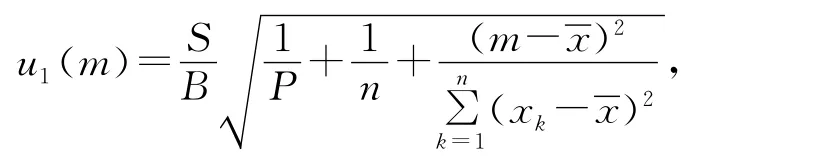
式中A为校准曲线截距；B为校准曲线斜率；p为测量样品次数；n为校准曲线浓度点测量次数；m为测量样品的平均值;为不同校准标准的平均值。

由此可得：残余标准偏差S＝0.013 2，u1（m）＝0.052 9，相对不确定度u1＝u1（m）／m＝0.008 94。4.2.2 配置标准溶液时所产生的不确定度u2

式中C贮为硫酸根标准贮备液的浓度，fi为稀释因子代表硫酸根贮备液稀释到使用液的稀释倍数。

以4.0mg／L标准溶液为例，将贮备液（500mg／L）按1∶10、再4∶50分两次稀释得到4.0mg／L标准使用液，这里1∶10稀释是采用10mL的无刻度吸管和100mL的容量瓶来完成，4∶50稀释是采用10mL刻度吸管和50mL容量瓶来完成，所以C0＝C贮×V10／V100×V10／V50。

其相对不确定度u2＝u（C0）／C0＝

（1）SO2-4标准贮备液测量的不确定度分析。标准贮备液是直接购买的有证标准物质，按标准值的2%给定最大允差，按近似正态分布（k＝2）转换成标准不确定度为

（2）10mL无刻度吸管取样产生的不确定度分析。10mL吸管的标准不确定度来源有3个：第一，吸管体积的不确定度，按制造商给定容器容量允差为±0.020mL，按照均匀分布换算成标准偏差为；第二，充满液体至吸管刻度的估读误差吸管和溶液的温度与校正时的温度不同引起的体积不确定度，假设温差为2℃，对水体积膨胀系数为2.1×10-4／℃则95%置信概率（K＝1.96）时，体积的变化区间为：±10×2×2.1×10-4＝±0.004 2mL转化成标准偏差为：0.004 2／1.96＝0.002 1mL，以上3项合成得出：u（V10）／V10＝［（0.0122＋0.0292＋0.002 12）1／2］／10＝0.003 1。

（3）100mL容量瓶不确定度分析。100mL容量瓶的标准不确定度来源有3个：第一容量瓶体积的不确定度，按照制造商给定容器容量允差为±0.10mL，按照均匀分布换算成标准偏差为＝0.058；第二充满液体至吸管刻度的估读误差，吸管和溶液的温度与校正时的温度不同引起的体积不确定度，假设温差为2℃，对水体积膨胀系数为2.1×10-4／℃则95%置信概率（K＝1.96）时，体积的变化区间为：±100×2×2.1×10-4＝±0.004 2mL转化成标准偏差为：0.004 2／1.96＝0.002 1mL，以上3项合成得出：u（V100）／V100＝ ［（0.0582＋0.2892＋0.002 12）1／2］／100＝0.002 9。

同理可得10mL刻度吸管不确定度为u（V10）／V10＝0.002 9，50mL容量瓶不确定度为u（V50）／V50＝0.003 2将以上5项不确定度分量代入公式得到：

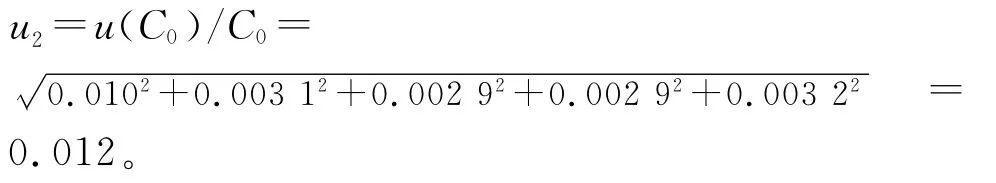
4.3 离子色谱仪的定量重复性引起的不确定度

色谱峰面积的标准测量不确定度分量主要是由离子色谱仪的定量重复性引起的不确定度，硫酸根分析使用的是离子色谱仪的电导检测器，定量重复性为0.8%，所以色谱峰面积的相对标准，不确定度为

4.4 合成不确定度的计算

4.5 扩展不确定度计算

扩展不确定度是用合成标准不确定度乘以给定概率的包含因子k而得，可以按中心极限定理估计接近正态分布时，采用t分布临界值由置信概率查t分布表得出k值，多数情况下采用p＝95%，可近似认为k95＝2，则扩展不确定度U＝2×uc（c）＝0.208。

5 结语

样品浓度为C＝5.92mg／L，扩展不确定度为0.208，包含因子k＝2，置信概率p＝95%。

［1］齐文启.环境监测实用技术［M］.北京：中国环境科学出版社，2006.

［2］国家环境保护总局编委会.水和废水监测分析方法（第四版）［M］.北京：中国环境科学出版社，2002.