基于JSCORS的全球海潮模型比较研究
董春来,蒋廷臣,周 立
(淮海工学院,江苏连云港222005)
基于JSCORS的全球海潮模型比较研究
董春来,蒋廷臣,周 立
(淮海工学院,江苏连云港222005)
针对沿海GPS高精度测量的要求,进行海潮模型的效用分析。基于JSCORS网站的基准信息数据,通过试验设计与GAMIT软件解算处理,绘图对比CSR4.0、SCHW80与FES2004等3种常用海潮模型的改化修正效果,并取得区域性选择海潮模型的合理结论。
JSCORS;海潮模型;GAMIT;比较研究
一、引 言
海洋潮汐是由于海水在太阳和月亮引潮力作用下所产生的周期性涨落现象。海潮负荷潮是指海潮对固体地球产生的影响,是海潮对GPS高精度测量的影响因素之一。20世纪以来,随着认知与研究的发展,人们对海潮精度的要求越来越高,拉普拉斯所创立的潮汐动力学理论,已难以满足时代发展的需要,因此一系列海潮模型应运而生。在沿海区域实施GPS高精度测量,必须考虑海洋潮汐变化对定位精度的影响,合理地选用全球海潮模型无疑是普遍关注的重要论题。本文旨在研究海潮模型对沿海GPS高精度测量的修正效果及适用性,为高精度海潮测量研究提供借鉴。
二、海潮模型的效用分析
根据Farrell理论,海潮负荷可由海潮的瞬时潮高与格林函数褶积积分算得,采用格林函数解法,求解海潮负荷对测站位移的影响,得到海潮负荷的各个方向变化模型为

式中,ΔU、ΔS、ΔW分别表示t时刻海潮负荷所产生的测站U向(径向)、S向和W向位移;ρ为海水密度; Hi(φ',λ')为积分面元第i个分潮波瞬时潮高;φ、φ'为测站积分面元纬度;λ、λ'为测站积分面元经度;A为测站到积分面元方位角;θ为球面角;Δ(φ,λ,t)表示测站位移负荷。通过Δ(φ,λ,t)可求出各分潮波位移改正的振幅与相位,再以此为基础,可以求得测站位移负荷变形,即
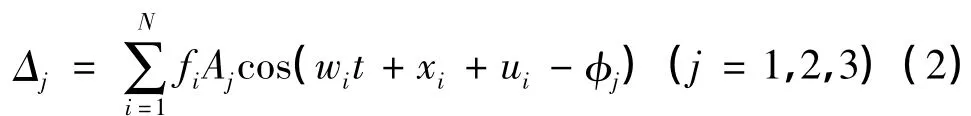
式中,Δj(j=1,2,3)分别代表测站S向、W向与U向海潮负荷变形;N为潮波总数;fi指与月球升交点经度相关系数;Aj指与测站第j个位移分量相适应的第i个分潮波振幅;wit+xi+ui为第i个分潮波于t时刻地球固体潮而造成的相位延迟,其中,wi为第i个分潮波角频率,xi为天文幅角数,ui为与月球升交点经度相关的参数;φj指格林尼治相位。
为了更好地与常用的直角坐标系统相结合,结合式(1)与式(2),解得三维直角坐标形式的位移变化ΔX、ΔY、ΔZ为

由式(3)可以看出,ΔX、ΔY、ΔZ的数值与海潮模型的选择有较大关系,表明海潮模型的选择会影响全部海潮负荷改正的整体质量。因此,进行海潮改正时,要求合理选择海潮模型,特别是符合区域沿海的海潮模型。
三、常用海潮模型基本信息比较
CSR4.0、SCHW80和FES2004海潮模型是目前普遍使用的3种全球海潮模型。其基本信息比较如表1所示。

表1 海潮模型基本信息
四、基于JSCORS的试验方案设计
为了推进江苏省信息化及测绘科技的发展,更好地服务于江苏省国民经济建设,JSCORS系统于2006年12月建成投入运行。至今,JSCORS系统包含有70个参考站点,其中,江苏省内67个,上海境内3个。参考站点间距最长83 km,最短12 km,平均50 km。为了研究沿海区域GPS测量的海潮影响状况,以江苏沿海CORS基站点为基础,以连云港周边基站点为参考,选取10个基站点构成GPS网。站点如表2所示,网点及基线如图1所示,基线总数为10×(10-1)/2=45条,基线号分别为1(BGDH-BTGU)、2(BGDH-BTGY)、3(BGDH-BTQD)、4(BGDHBTRD)、5(BGDH-BTDF)、6(BGDH-BTUZ)、7(BGDHDZXY)、8(BGDH-GTBH)、9(BGDH-GTYW)、10(BTGU-BTGY)、11(BTGU-BTQD)、12(BTGU-BTRD)、…、43(DZXY-GTBH)、44(DZXY-GTYW)、45(GTBHGTYW)。

表2 基站点名和代码
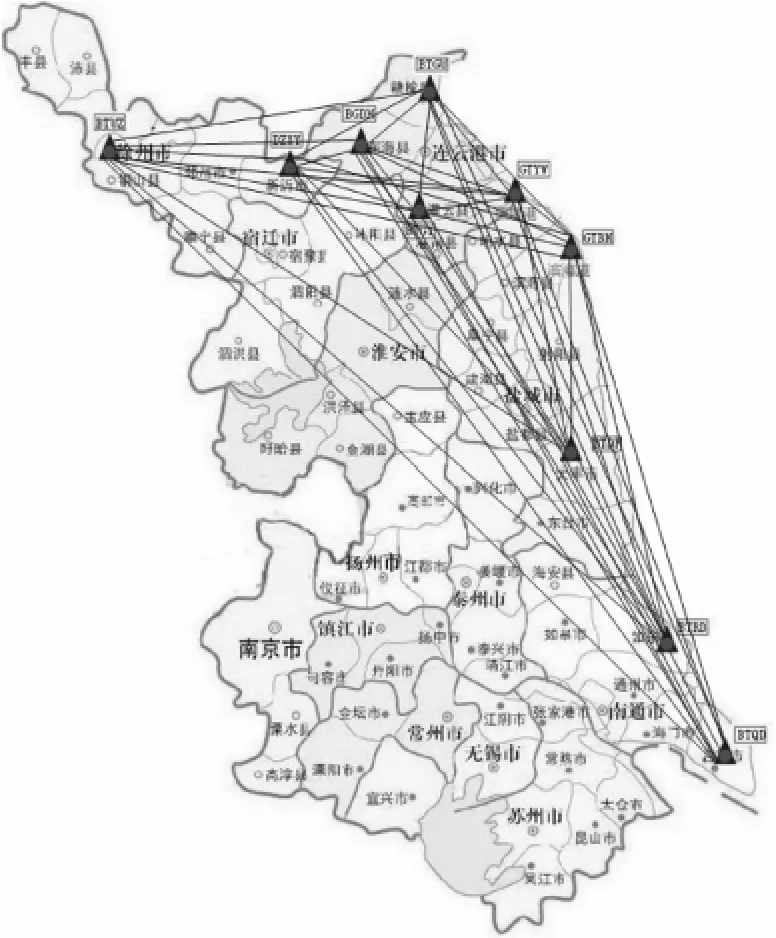
图1 试验方案站点及基线图
五、海潮模型改化效果的比较分析
为了减小海潮对GPS高精度测量的影响,加入海潮模型改正是非常必要的,试验以江苏CORS基站为例,探讨适合于江苏沿海特别是连云港沿海GPS测量的海潮影响改正模型。利用Excel对比分析CSR4.0、FES2004、SCHW80两两海潮模型改正对基线坐标分量的偏差,如图2~图4所示。

图2 SCHW80与FES2004对基线向量改正偏差

图3 CSR4.0与FES2004对基线向量改正偏差

图4 CSR4.0与SCHW80对基线向量改正偏差
对比分析图2、图3和图4可知:
1)使用不同的海潮模型对GPS基线的改正是不相同的。在图2中,SCHW80与FES2004全球海潮模型的X方向的差值最大可达1.2 mm,Y方向的差值可达3 mm,Z方向的差值可达1.2 mm;在图3中,CSR4.0全球海潮模型与FES2004全球海潮模型的X方向的差值最大可达1 mm,Y方向的差值可达0.5 mm,Z方向的差值则小得多,仅有0.2 mm;在图4中,CSR4.0全球海潮模型与SCHW80模型的X方向的差值可达1 mm,Y方向的差值可达3 mm,Z方向的差值达到1 mm。
2)海潮模型对GPS基线向量的不同改正分量也不相同。在图2中,GPS基线向量的改正方向主要体现在Y方向上;在图3中,GPS基线向量的改正方向主要体现在X方向上;在图4中,GPS基线向量的改正方向主要也体现在Y方向上。可见不同的海潮模型对GPS基线向量的改正存在着差异。
六、结束语
海洋潮汐作为沿海GPS高精度测量的关键误差来源之一,在实施GPS高精度测量过程中必须合理选择海潮模型。本文比较研究了修正海潮对GPS测量影响的CSR4.0、SCHW80与FES2004 3种海潮模型,运用分析软件包GAMIT及现代计算方法,基于沿海江苏CORS参考站单网,试验分析了CSR4.0、SCHW80与FES2004 3种海潮模型修正效果。结果表明:
1)高精度GPS测量必须加入海潮模型改正,海潮对GPS测量基线坐标分量的影响不同,一般来说,Z方向最小,X方向次之,Y方向最大。
2)尽管海潮模型差异很小,但是仍存在差异,实施沿海高精度GPS测量,选择适合局域的海潮模型,对于江苏沿海GPS测量来说,选用FES2004模型实施海潮影响改正较为有利。
[1] 周旭华,吴斌,李军.高精度大地测量中的海潮位移改正[J].测绘学报,2001,30(4):327-330.
[2] 张捍卫,郑勇,赵方泉.海洋负荷潮汐对测站位移影响的理论研究[J].大地测量与地球动力学,2003,23(1):69-73.
[3] 周江存,孙和平.近海潮汐效应对测站位移的负荷影响[J].地球物理学进展,2007,22(5):1340-1344.
[4] 陈宪冬.GPS精密定位中的海潮负荷改正[J].西南交通大学学报,2006,41(4):429-432.
[5] 许军,暴景阳,刘雁春,等.潮汐模型对利用卫星测高数据研究海平面变化的影响[J].武汉大学学报:信息科学版,2006,31(6):503-507.
[6] 袁林果,丁晓利,孙和平,等.利用GPS技术精密测定香港海潮负荷位移[J].中国科学:地球科学,2010,40(6):699-714.
A Comparative Analysis of Global Ocean Tide Model Based on JSCORS
DONG Chunlai,JIANG Tingchen,ZHOU Li
0494-0911(2012)08-0001-03
P731
B
2012-03-14
江苏省海洋资源开发研究院开放基金(JSIMR10C01)
董春来(1963—),男,安徽安庆人,副教授,主要研究方向为大地测量及数据处理。

