独立分量分析在煤仓沉降分析中的应用

赵国忱，苏运强，范 良

(辽宁工程技术大学测绘与地理科学学院，辽宁阜新123000)

独立分量分析在煤仓沉降分析中的应用

赵国忱，苏运强，范 良

(辽宁工程技术大学测绘与地理科学学院，辽宁阜新123000)

煤仓是煤炭生产中重要的建筑物，因其装载大量的煤炭，故需对其进行沉降观测，观测的主要方法是高等级水准测量。独立分量分析是一种在信号组成成分未知的情况下，将信号分为几个相互独立的成分的数学方法。将独立分量分析用于煤仓沉降数据的分析，比较可能会对煤仓沉降产生影响的几个因素，并获得成分之间的对应关系。

煤仓;沉降观测;独立分量分析;FastICA算法

一、引 言

内蒙古自治区鄂尔多斯市某煤矿是设计年产千万吨级的大型煤矿，于2011年年初正式投产，其工业广场上建有原煤仓、沫煤仓、精煤仓和矸石仓总计10个，其中，装载量最大的是两个2.5万吨的沫煤仓。为保证煤仓运行的安全性，需要定期对其进行沉降变形观测。

二、观测方法

煤仓建设时，建设单位在每个煤仓圆形基础上对称设置了4个沉降观测点。由于厂区面积较小，周边地势坡度较大，不利于建立两级沉降观测控制网。在厂区内部尽量远离煤仓，而且在采动影响范围外的位置建立了3个沉降控制点，作为观测基准点。定期将沉降观测点和厂区内的某一沉降观测基准点进行联测。计算各个点的沉降量，同时定期将沉降观测基准点与厂区外的国家控制点联测，检核其准确性。

沉降观测使用Leica DNA03电子水准仪，按照二等水准测量的要求进行，观测周期为10天。从2010年4月到2010年11月，进行了多次观测，获取了沉降数据和装煤量的数据。观测数据表明在该观测时间段内，煤仓的运行是安全的，煤仓的沉降也与装煤量表现出了明显的正相关关系，如图1所示。

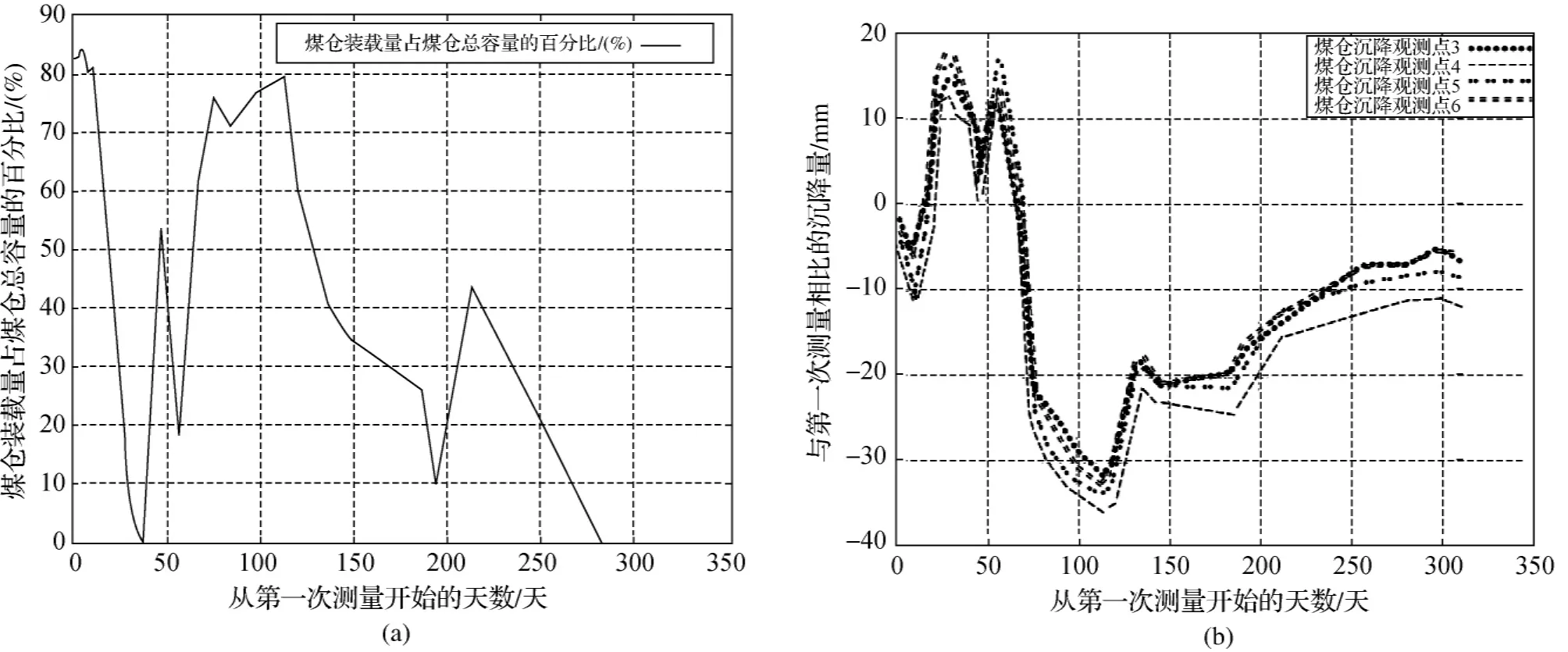
图1 一号沫煤仓的装煤量和沉降量关系图

三、独立分量分析

1.独立分量分析的历史和应用

独立分量分析是一种统计和计算机技术，用于揭示随机变量、测量数据或信号中的隐藏成分。该技术于20世纪80年代初期首先在神经网络建模领域中引入，20世纪90年代引入一些极为成功的算法，解决了一系列问题，典型的如鸡尾酒会问题。它在神经网络领域(特别是无监督学习)中成为一个非常重要的方法。独立分量分析在生物信号处理、语音信号分离、无线通信、故障诊断、特征提取、金融时间序列分析和数据挖掘等现实领域中得到了广泛的应用［1］。

所谓鸡尾酒会问题，即多个人同时说话，同时有多个录音设备将其录下，如何使用数学方法，将不同人的声音区分开来。其最简单的情形是说话的人数和录音设备的数量相同，比如都是4个，因为不同人的声音到达每个录音设备的时间不同，根据各个录音设备记录时间差将不同来源的声音进行分离。

2.独立分量分析的基本原理

独立分量分析是所谓盲源分离或者盲信号分离问题的一种解决方法。“源”是指原始信号，即独立分量，如鸡尾酒会问题中的说话者;“盲”表示对所研究的问题知之甚少，所能依据的仅仅是几条假设。

对于一个问题，假设其有n个因子，用s表示，称为源信号。与此同时，可以观测到一系列信号，用x表示，称为观测信号。s和x有一定的关系，现在假设此关系为线性关系，用矩阵A表示此关系，称为混合矩阵，于是

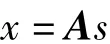
现在由于s、A均未知，就要根据一定的假设，在某种极值条件下得出对s的某种估计。

独立分量分析的几个假定包括:假定独立分量统计独立、独立分量的分布具有非高斯性、假定未知的混合矩阵是方阵(即观测数量和源信号数量相等)。

几种可用的极值条件有极大非高斯性、极大似然、极小化互信息等。

但是，独立分量分析也有两个含混因素，即无法确定独立分量的方差、无法确定独立分量的次序。

3.FastICA算法

FastICA算法是解算独立分量分析的一种具体算法，也称为固定点算法。该算法是基于定点递推算法得到的，对任何类型的数据都适用，同时它的存在对运用ICA分析高维的数据成为可能。

FastICA算法的优点有:收敛速度快;不需要选择步长，更容易使用;通过使用一个非线性函数便能直接找出任何非高斯分布的独立分量;性能能够通过选择一个适当的非线性函数而达到最佳;独立分量可被逐个估计出来，在探索性数据分析里是非常有用的。

四、独立分量分析应用于煤仓沉降数据处理

1.基本思想

假设有4个相互独立的因素对煤仓的沉降产生了影响，如温度、装煤量、时间、装载时的不均匀程度。将这几个因素当做源信号，即类比成鸡尾酒会问题中的说话者。将每个煤仓上的4个点测得的沉降量当做4个观测到的信号，即类比成鸡尾酒会问题中记录下的声音。

使用FastICA算法对煤仓的观测序列进行分析，得到分离后的4个独立分量。比较得到的独立分量和可能的影响因素之间的关系。

2.结果分析

根据以上方法，使用Python语言和Python语言的数据处理模块工具集(Modular toolkit for Data Processing)编写程序，处理数据后绘得图2。

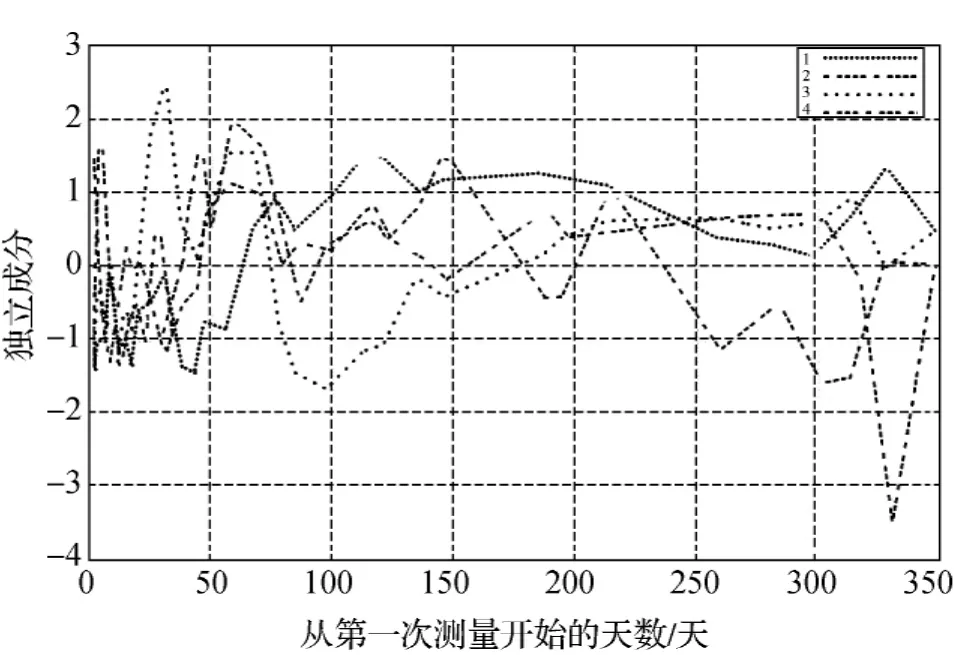
图2 FastICA分析得到的4个独立分量

对比装煤量、当地平均气温、观测时间等信息，比较图中的4个分量，可以得出如下结论:

1)煤仓刚投入使用的时候，各分量变化比较混乱。

2)后期大体可以认为3号线条表示因为时间变化而产生的塑性下沉。因为随着时间的变化，其逐渐增大，到后期已经基本不变。

3)4号线条走势和装煤量的走势基本相同，可以认为是因装煤而产生的弹性下沉。

4)2号线条的后期走势和当地气温比较符合，可以认为是气温对沉降产生的影响。

总的可以看出，对沉降产生影响最大的还是装载量。现在煤仓已经基本稳定，不会因为时间的推移继续下沉，总的下沉量也比较小，可以认为地基处理还是比较好的。

五、结束语

从以上的分析和图2可以看出，各种环境因素对煤仓沉降的定性影响基本符合预期。

但是由于观测的时间还比较短，可能与实际情况有较大差异，需要更多的数据来确定这种关系，以上分析只是定性分析，还不能给出各个因素对沉降的具体影响的大小。使用的线性的独立分量分析，或许与实际情况不完全符合。因此需要进一步对该煤仓的沉降进行跟踪观测，对数据进行定量分析，使用非线性独立分量分析代替线性的独立分量分析，进而获得沉降量与各种影响因素的定量关系。

［1］ AAPO H，JUHA K，ERKKI O.Independent Component Analysis［M］.Hoboken:John Wiley＆Sons Inc.，2001.

［2］ ZITO T，WILBERT N，WISKOTT L，et al.Modular Toolkit for Data Processing:a Python Data Processing Framework［EB/OL］.2008-08-26［2011-10-12］.http:∥www.frontiersin.org/neuroinformatics/10.3389/neuro.11.008.2008/abstract.

［3］ 赵少荣，陶本藻，于正林.论变形测量数据的反演［J］.测绘学报，1992，21(3):161-172.

［4］ 冯延明.监测水准网的滤波方法［J］.武汉测绘科技大学学报，1987，12(1):14-25.

［5］ 吴冰.基于ICA和小波变换的过程监测方法的研究［D］.沈阳:东北大学，2008.

［6］ 刘喜武，刘洪，李幼铭.独立分量分析及其在地震信息处理中应用初探［J］.地球物理学进展，2003，18(1): 90-96.

［7］ 王刚，胡德文.独立分量分析对相关信号源的盲辨识性能分析［J］.计算机工程与应用，2005(4):23-26.

Application of Independent Component Analysis in Settlement of Coal Bunker

ZHAO Guochen，SU Yunqiang，FAN Liang

0494-0911(2012)06-0016-03

P258

B

2011-10-11;

2012-02-17

赵国忱(1962—)，男，辽宁辽中人，教授，主要从事变形监测与预报、沉陷治理、数字化测图技术等方面的研究工作。