基于已知两个方向角的相对位姿标定

陆义云

（南京邮电大学 自动化学院，江苏 南京 210046）

0 引言

多个点的PnP问题已经得到很广泛的研究，对于所谓的PnP问题[3]，在计算机视觉一般描述为：给定一个世界坐标系中的已知点集和它们在像平面对应的投影，求在世界坐标系和摄像机坐标系之间的变换矩阵（3个旋转参变量和3个平移参变量）。由于PnP问题在目标跟踪、物体识别、视觉导航等许多领域有着广泛的应用前景，因此一直是计算机视觉中的一个重要问题。目前，在计算机视觉方面，对于PnP问题的研究存在许多方法，比较流行的有P3P问题和P4P问题,对于P3P问题解的研究也取得了众多的成果。在国内，2006年吴毅红等利用正交变换下求解正解等价于求解基于变换定义下的旋转矩阵和平移向量；不过吴毅红等只指出了解的上限，没有作详细的证明；在国外，Zuzana Kekelova[15]等人对于基于未知焦距的P3P问题也作了研究[13]。对于P4P问题的研究，T.Pajdla[13]等人提出了基于未知焦距的P4P方法，Bujnak M[14]等人提出了基于未知焦距和径向畸变的P4P问题的方法。但无论是基于3点的PnP问题还是基于4点的PnP问题，它们有一个共同的缺点，就是要求的计算量都比较大，运算速度比较慢，此外还会受到各种条件的影响。本论文中提供了一种基于2点的PnP的方法来求解相机的旋转矩阵和平行向量。

本文中，研究已知两个方向下相对位姿标定问题的计算。它主要是受到手机重力感应技术和装有惯性测量单元（IMU）的智能手机（如NOKIA, iPhone）启发。在智能手机中主要是由加速度计测量地球重力矢量测量到两个方向角度（如在iPhone中采用的加速度计是3轴加速度计，分别X，Y和Z轴，这3个轴构成的立体空间以侦测你在iPhone上各种动作，实际应用时通常以这3个轴或任意两个轴所构成的角度来计算iPhone倾斜的角度[0]）。本文中给定的P2P问题，最终转化为求解多项式方程组的问题，通过利用Grobner基法[2，9]求解。

1 相机标定

摄像机的基本成像模型，通常称为基本针孔模型，由三维空间到平面的中心投影变换所给出，令空间点Oc是投影中心，它到像平面π的距离为f，空间点X在平面π上的投影（或像）u是以点Oc为端点并经过Xw的射线与平面π的交点[1,11]，则由空间点Xw到图像点u的投影矩阵可以写成：

P是3×4投影矩阵，其可表示成 ：

其中，λ为深度因子，K为摄像机内参矩阵，t=[tx,ty,tz]T为平移向量，R是一个3×3的正交矩阵，对于摄像机内参矩阵K，可以写成：

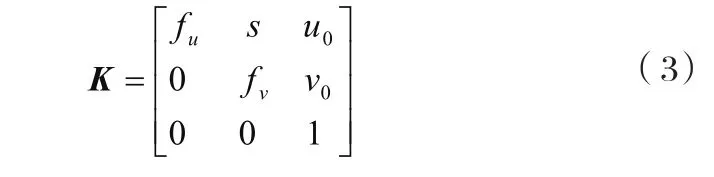
式（3）中fu为图像横坐标轴尺度因子，fv为图像纵坐标轴尺度因子。s为歪斜因子，表示两个坐标轴的垂直程度，（u0,v0）表示主点横坐标和纵坐标。

对于旋转矩阵R，在三维空间中，可以用欧拉角（α、β、γ）来表示，其中α（也称roll）为绕Z轴旋转角，γ（pitch）为绕X轴旋转角，β（yaw）为绕Y轴旋转角，R可以写成：

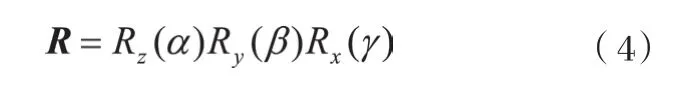
其中：绕Z坐标轴旋转矩阵为：

绕X坐标轴旋转矩阵为：

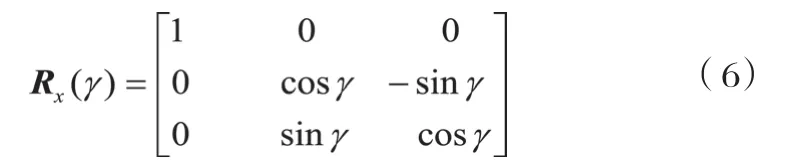
绕Y坐标轴旋转矩阵为：

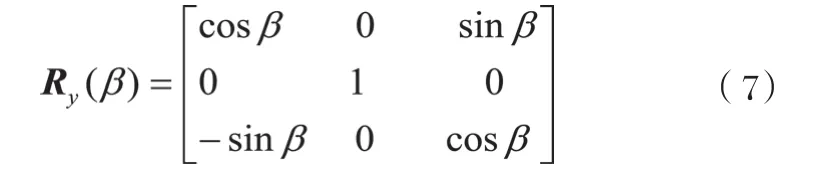
现在基于重力感应的手机（如iphone，NOKIA等）可以利用加速度计测量地球重力矢量来测量到两个方向角度，即可测量到绕Z坐标轴的旋转角α和绕X坐标轴旋转角γ。对于一个P2P问题的摄像机，其绕X和Z这两个坐标轴转动的角度为Roll和Pitch，即垂直方向已知，求摄像机的绝对位置。因此在式（4）中β是唯一的参数。

对于尺度因子λ的消去，通常采用反对称矩阵[u]×与方程相乘的方法，因此可以得到：

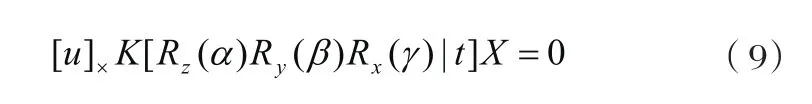
其中反对称矩阵为：

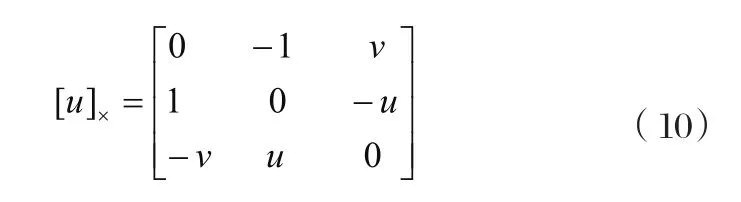
因此式（9）可以写成：

在式(10)中，由于对称矩阵的秩为2，因此在（11）式得到的3个多项式方程中，其中2个是线性不相关的。在这3个多项式方程组中，含有q2，q，tx，ty，tz这几个变量。在此，可以运用Grobner基的方法求解多项式方程组。

2 Grobner 基求解多项式方程组

代数方程组的求解是许多领域中经常要处理的问题，而当变元很多时,求解过程往往比较困难。为此，我们可以使用Grobner基[2-3,5]的方法求解代数方程组。

将多项式加上“=0”即变成方程组，所以方程组和多项式的关系是非常密切，为了解多元多次方程组的问题，我们可以考虑将它转化为多项式问题。同时有必要定义个一个多元多次多项式中每个单项的排列次序，即单项式的大小[4,6,8-9,11]。在这方面一般定义方法为：

定义：

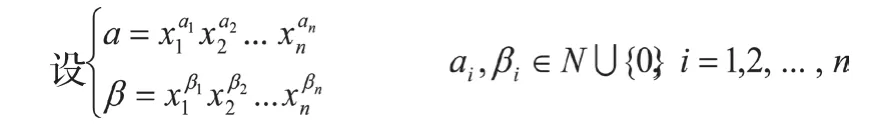
定义两个单项式的大小顺序为x1＞x2＞…xn，再者，同一未知数定义xm+1＞xm＞…x2＞x＞1，我们称α＞β，这种次序大小称为字典序（简称lex order）。

定义：设K是一个域，k[x1,x2,…,xn]为系数属于K的n元多次多项式所成集合，即：

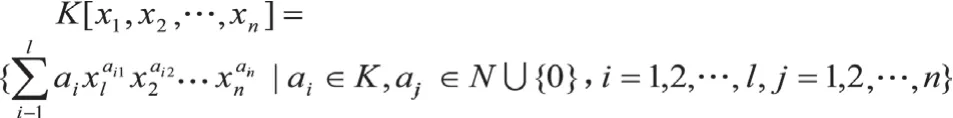
（a）0∈I；

（b）若f,g∈I，则f+g∈I；

（c）若f,g∈I，且则。

定义：

lp(f)=X a1，即lp(f)表示f的首项幂积；

lc(f)=a1，即lc(f)表示f的首项系数；

lt(f)=a1X a1，即lt(f)表示f的首项；

假设域K上的多项式方程组Pi(X)=0,i=1, 2, …,m，要求解这样一个方程组，需要解决一些问题：该方程组有多少解，怎么求解。考虑由该方程组的多项式生成一组理想，计算某字典序下的Grobner基G，则上述的多项式方程组问题可以通过G来求解，下面给出方程组的求解方法，设给定域K[X]中的一个方程组：

Pi(X)=0,i=1, 2, …,m；

选取字典序x1＞x2＞…xn，计算理想[2]＜p1,p2,…pm＞ 的Grobner基G={G1,G2, …,Gr}，对G中的多项式适当排序后，存在Gi∈G,与mi使得lp（Gi）=，i=1,2,…,n,则必有n≤r，在字典序[2]x1＞x2＞…x下，lp（G）=，Gn的其它项也必含xn，即Gn是xn的一元多项式。同理Gn-1仅xn-1,xn类推下去，可知G包含如下多项式方程组：

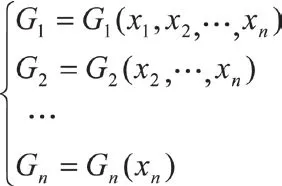
由最后一个方程Gn=0解一组xn的解（an1,an2,…,anl），再将每个ani(i=1, 2, …,l)代入Gn-1以及其它G中仅含xn-1，xn的多项式Gj=（xn-1,xn）=0,…,可得xn-1的方程组Gn-1=（xn-1,ai）=0，Gj=（xn-1,anj）=0, …，仍然是一个一元多项式方程组，解之又可得到对应xn-1的解，继续下去即可得到原方程组的全部解。

3 仿真及分析

本文运用Grobner基算法，采用的图像如图1所示，使用iphon4手机拍摄测试图片，在拍摄测试图片时，经过一定计算可得，摄像机绕Z坐标轴选择角度约为 pitch=-139.41°，绕 X坐标轴旋转角度约为roll=25.83°，建立如图1所示的三维坐标系，选取3组2D-3D对应点，图像点 A坐标（129.1875,634.9875）对应空间点坐标（130,0,0）。图像 C 点（664.1250,350.1250）对应空间点坐标为（130,66,0），图像 D 点坐标（1424.9755，1769.3000）对应空间点为（0,66,146），其中D点作为验证点，此时已知相机的内部参数矩阵为：

选取A点和C点作为测试点，利用Groebner基求可得解约为：

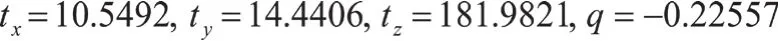
即此时绕Y坐标轴旋转角度约为yaw=-25.42，此时旋转矩阵为：

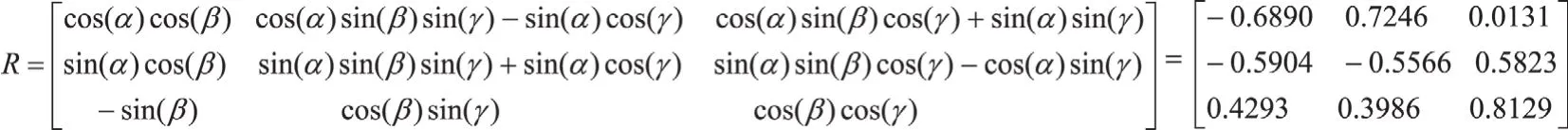
平移向量为T=[10.5492 14.4406 181.9821]

将D点代入到其中验证可得D点的重投影在图像上的坐标为（1420.9671,1768.2998），即所得点的坐标在误差允许的范围之内。

图1 测试用图

4 结论

计算机视觉中，PnP问题的应用越来越广泛，本文中利用一些设备来获取两个角度，并利用2组2D-3D的对应点来解决PnP问题，与传统的PnP问题相比，其在求解速度上有了很大的提高，而且更方便，现在的智能手机几乎都安装有惯性测量单元，其利用重力感应能测量手机的在空间中方位，此外在一些导航设备（如GPS）上都有应用。

计算机视觉中，PnP问题的应用越来越广泛，因此能否快速且有效得解决PnP 问题对计算机视觉中许多问题起着很重要的影响（如三维重建等），本文中利用一些设备来获取两个角度，并利用2组2D-3D的对应点来求解旋转矩阵和平移向量，与传统的求解PnP问题相比，其在求解速度上有了很大的提高。随着社会的发展，智能手机的运用也越来越广泛，现在的智能手机几乎都安装有惯性测量单元，其利用重力感应能测量手机的在空间中方位，并且现在的许多手机游戏都用到了惯性测量单元，此外在一些导航设备（如GPS）上都有应用。

[1]马颂德,张正友.计算机视觉[M].北京:科学出版社,1998.

[2]刘木兰.Grobner基理论及其应用[M].北京:科学出版社,2000.

[3]汤建良,高小山.透视n点定位（PnP）问题研究[D].中国科学院研究生院,2004.

[4]李源顺.浅谈多元多次方程[J].数学传播,2003.

[5]吴福朝.计算机视觉中的数学方法[M].北京:科学出版社,2008.

[6]刘侍刚,吴成柯.高精度三维重建技术的研究[D].西安:西安电子科技大学,2005.

[7]彭丰富.Grobner基与约化的研究及其应用[D].长沙:中南大学,2001.

[8]D.Martinec,T.Pajdla.Robust Rotataion and Translation Estimation in Multivie Reconstruction[J].In CVPR,2007.

[9]Bruno Buchberger,Grobner Bases.A Short Introduction for Systems Theorists[J].Computer Aided Systems Theory EUROCAST,2001.

[10]Zuzana Kukelova.MartinBujnak.Tomas Pajdla.Closed-form solutions to the minimal absolute pose problems with known vertical direction.[J]. In:ACCV 2,Vol.6493Springer:216-229.

[11]Martin Byrod ,Klas Josephson.Kalle Astrom Fast and Stable Polynomial Equation Solving and Its Application to Computer Vision [J]. Int J Computer Vision,2009,84:237-256.

[12]B.Buchberger.An Algorithmical Criterion for the Solvability of Algebraic Systems of Equations (German)[C].Aequationes Mathematicae,1970,4(3):374-383.

[13]M. Bujnak,Z.Kukelova,T.Pajdla.A general solution to the P4P problem for camera with unknown focal length[C]. CVPR 2008, Anchorage, Alaska, USA, June 2008.

[14]Bujnak M,Kukelova,Z.,Pajdla,T.A general solution to the P4P problem for camera with unknown focal length[C]. In Proceedings of CVPR. 2008.

[15]Kukelova Z.,Bujnak M.,Pajdla T.Closed-form solutions to the minimal absolute pose problems with known vertical direction[C].ACCV 2010, Queenstown, NZ,2010,November:8-12.