Wigner-Ville分布在电力系统低频振荡中的应用

胡 思

（电子科技大学自动化工程学院，四川成都 611731）

0 引言

电力系统运行机组间有时会出现功率振荡的问题，振荡频率的范围在0.2～3 Hz，因此称为低频振荡。随着电力系统规模的不断扩大、互联以及大型机组快速励磁系统的采用，低频振荡问题日益突出，严重地威胁着电力系统的安全稳定运行。

在高维非线性动态电力系统中，其时间响应信号往往表现为一种典型的非平稳过程，即信号的统计特性(包括时域统计特性和频域统计特性)随时间的变化特性[2-4]。其原因是低频振荡的暂态过程中往往共存着多个不同的非线性模式，各振荡模式间存在或强或弱的相互作用，从而衍生出新的振荡模式[5-6]，从系统非线性变化特性的角度来看，低频振荡过程一定具有时变特性[6-7]。

目前对于电力系统低频振荡信号分析的问题已有过大量的研究，也提出了很多算法。分析方法有傅里叶算法、Prony算法[8]、小波算法等。傅里叶算法是一种全局的变换，无法反映振荡的阻尼特性及瞬时频率问题，而这是非平稳信号最根本、最关键的性质。传统Prony算法的拟和结果对噪声很敏感，且阶数难以确定。针对以上问题，某些学者提出了一些解决办法并做了有益的改进[9-11]。但是在非平稳信号的处理上，Prony算法仍不能提供信号的频率时变特性和局部特征的时变特性[12]。小波算法能将时域和频域结合起来描述观察信号的时频联合特征，构成信号的时频谱，可以反映振荡的时变特性。但小波变换的分析分辨率仍存在一定的极限。

作为一种优良的时频分析方法，Wigner-Ville 分布能够精确地估计出电力系统低频振荡信号的幅值和频率参数[13-16]，相对于其它的联合时频分析方法，具有简洁、有效，分辨率高，能量集中性和跟踪瞬时频率的能力强等优点，可以清晰地表征信号在时频域内的变化。

本文提出应用WVD对电力系统低频振荡信号进行分析的方法，该方法能够精确地估计出电力系统低频振荡信号的幅值和频率参数。

1 Wigner-Ville分布

WVD分布是Cohen类双线性时频分布一种，它以自相关函数相对时间位移为积分变量对信号自相关函数作傅里叶变换，从而得到的关于时间和频率二维线性函数其定义为：

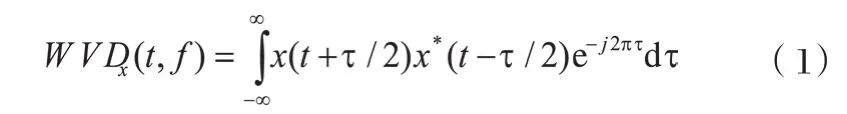
其中x(t)是实际信号s(t)的复频率信号，借助Hilbert变换（HT）将原信号移相90°组成解析信号[14]：

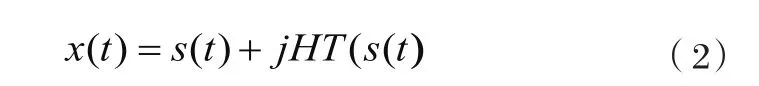
采用解析信号能保证频谱为正，避免采样序列复频率谱线带来畸变。

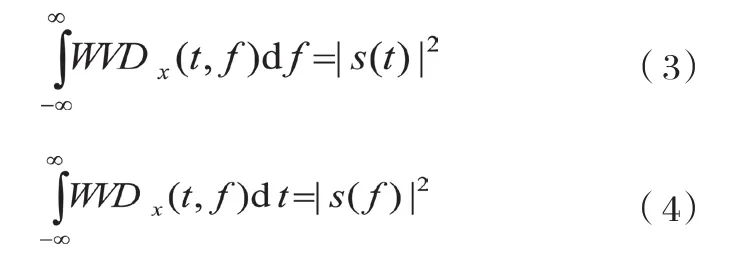
式（3）和（4）分别表示为WVD的时间边缘特性和频率边缘特性。其中|s(t)|2表示每单位时间的能量强度，|s(f)|2为每单位频率的能量强度。

WVDx(t,f)所表示的能量等于实际信号的能量，可视为一种时间和频率的能量强度函数。

2 离散WVD分布及低频振荡信号分析原理

低频振荡信号是一种非平稳信号，对于非平稳信号，需描述频谱含量与时间变化的关系。信号的时-频分布弥补了时间和频率描述的缺点，不仅提供了信号时间与频率的信息，还可以清楚地表示频率与时间的线性变化关系。

低频振荡的暂态过程中往往共存着不同的非线性模式，各振荡模式间存在相互作用，从而产生了更多的振荡模式。而WVD方法的一个重要特征是它能将复杂成分进行识别、分离并加以描述。

离散Wigner-Ville分布的定义为：

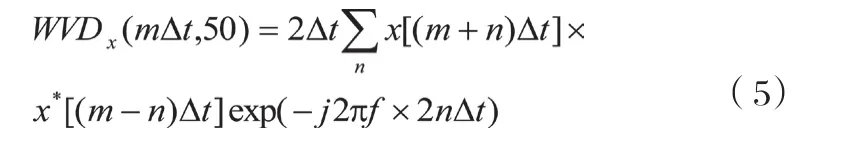
式（5）中：m=1,2,…,N；N为采样点数；Δt为采样时间间距；nΔt为自相关函数的时间延迟。设电网信号采样序列：

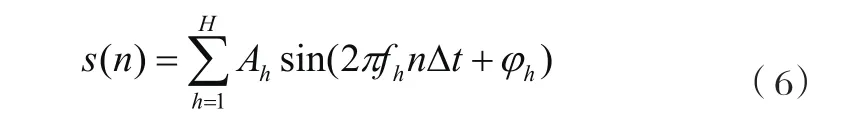
式中：n为采样点数；Δt为采样时间间距；Ah为信号幅值；φh为谐波初时相位，共有H个信号模式。对h模式信号分量，Wigner-Ville分布的信号项为：

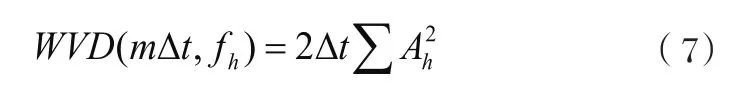
根据(4)所述的频率边缘特性可得：

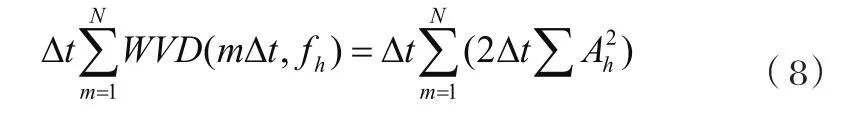
则h模式信号分量的幅值为：

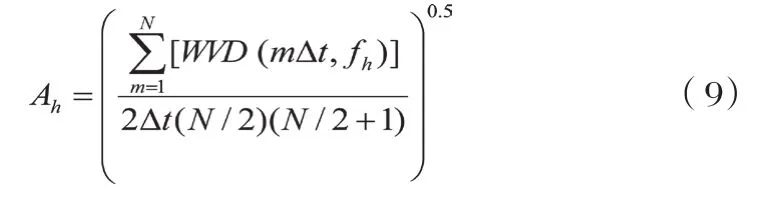
对时域仿真或实测振荡信号x(t)进行希尔伯特变化得到解析信号。解析信号经过WVD计算，得到原信号WVDx(t,f)的值，在时间-频率平面(t-f平面)上形成二维的信号能量时频分布图。当信号没有振荡时，信号的能量理论上是没有变化的。因此我们可以根据信号在时域和频域上能量的变化得知该信号的振荡特性。信号能量时频分布图较为精确地描述了信号的能量随频率和时间的分布情况，它对各振荡模式间的非线性相互作用刻画得非常细腻。

由式（7）可以准确计算该信号各模式的振荡幅值，由谱峰检测方法可以得到各模式的振荡频率。基于时频分布（TFD）的谱峰检测方法，采用时间和频率的联合函数来描述信号的频谱(或能量谱)特征。时频分布法具有良好的时频局部聚集性，WVD具有最理想的时频聚集性，这种谱峰检测方法的精确度高，具有良好的抗噪声能力。利用数学算法，对时-频分布图中的谱峰位置进行搜索，对应的即为信号的瞬时频率。同样由谱峰检测法可以得到各模式振荡信号的主导时间。

3 WVD算法仿真实例验证

3.1 算例1

构造一个由3个时间段组成的测试信号，将结果与已知值比较，从而考核WVD算法的准确性，其各段振荡波形具有不同的频率、阻尼和振幅(见表1)。

表1 测试信号组成

根据式（2）将该测试信号进行希尔伯特变化得到解析信号。采样频率为10 Hz，取256个采样点。

采用本文方法，计算得到256×256 Wigner-Ville分布矩阵。其频率分辨率为0.04 Hz。最高能分辨由式（3）对分布矩阵进行处理，得到的信号能量谱线图如图1所示。

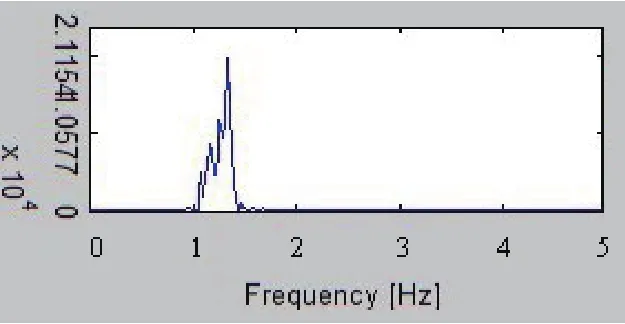
图1 测试信号能量-频率分布

信号谱图频率段1～1.5 Hz有明显的能量变化，有3个能量波峰，说明该频率段有振荡存在。由谱峰检测法计算图中 3 个能量尖峰分别出现在 1.152，1.250，1.328频率处，说明该振荡信号的主导频率为1.152 Hz，1.250 Hz，1.328 Hz。结果与测试信号主导频率值非常相近。

图2为时间-频率平面（t-f平面）上形成的二维的信号能量时频分布图。由该图可以清晰地观察得到信号随时间和频率的能量变化。利用式(9)可以计算各模式信号的幅值，而根据谱峰检测法可以计算各模式的主导时间。计算结果如表2所示。

图2 测试信号能量-时间-频率分布

表2 WVD分析结果

由表2结果可以得知，WVD时频分析方法较为精确的测得3个模式下信号的振荡频率，振荡幅值，各模式振荡信号的主导时间等信息。

3.2 算例2

用WVD方法从广域测量系统中提取电力系统动态特性的步骤是：

1) 将扰动后系统轨迹分群。

2) 对该信号进行希尔伯特变化得到解析信号。

3) 进行WVD分析。

4) 分析时间频率能量谱图。

5) 求取模式参数。

以实际电网中主要远距离交流联络线为分析对象，某时刻有功率时变信号x(t)如图3所示。

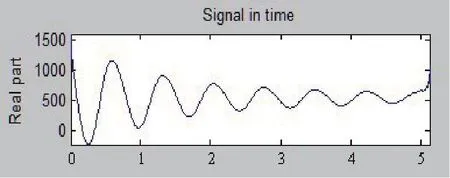
图3 x(t)信号时间-幅值分布

由图3可得知该信号为一个幅度衰减的低频振荡信号。信号的采样频率为100 Hz/s，时间选取5 s，将该信号进行WVD分析，如图4、图5所示。

由于时频分布的边缘效应(在信号的起始和结束段不能获得高度聚集的时频分布)，如图4、图5所示。故在边缘处的IF(瞬时频率)估计偏差较大，在假设整个观测时间内信号的IF都存在的基础上，以信号中间部分的IF估计值外推出信号起始段和结束段的少量IF值，这样不但可以提高估计精度，还可以缩短运行时间。由图中可以看出，在频率段0～5 Hz，有一个明显的能量波峰，随着频率的变大，信号能量趋于稳定。

同样由式（5）可计算得该信号振荡幅值为3.085×102。利用谱峰检测方法可得主导频率为1.38 Hz。

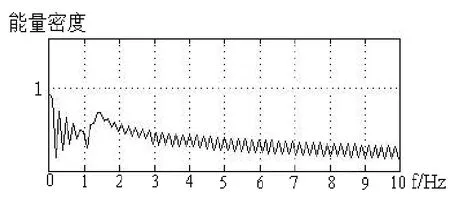
图4 x(t)信号能量-频率分布

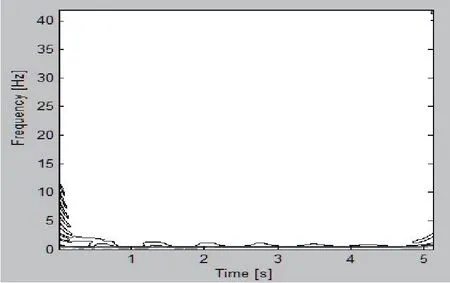
图5 x(t)信号能量-时间-频率分布

为比较和说明WVD算法的有效性，用Prony算法进行信号分析，结果如图6所示。

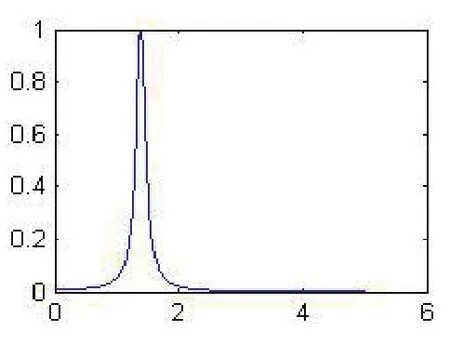
图6 x(t) Prony分析结果

图中横轴为频率，纵轴为归一化幅值。计算得主导频率为 1.287 Hz，幅值 3.075×102，阻尼系数为 -0.56。

综合比较WVD和Prony方法在该实际系统算例中的分析结果，发现前者可以反映信号的频率瞬变特性和局部特征中的时变特性。

值得注意的是，由于WVD是双线性形式的变换，因此叠加信号和的分布将存在交叉项。WVD自项和交叉项会有多种组合形式，同时交叉项可能出现在自项的位置，使得自项分布受到干扰。观察图2可以发现，图中存在交叉项的干扰。在基于时-频分布的瞬时频率估计中，交叉项的存在会影响对频峰正确位置的检测。

4 结论

本文研究了WVD方法在电力系统低频振荡问题分析中的应用。实例分析表明，该分析方法相对传统分析方法，能够很好地表现信号的局部特性及其变化规律、突出信号的瞬时频率变化，可实现系统动态振荡特性以及故障暂态信息的准确提取，为振荡机理研究奠定基础。

[1]王铁强, 贺仁睦,王卫国,等.电力系统低频振荡机理的研究[J].中国电机工程学报,2002,22(2):21-25.

[2]张贤达.现代信号处理[M].北京:清华大学出版社,1995.

[3]Kundur.P Power System Stability and Control[M].MacGraw-Hill.Inc.,1994.

[4]卢强,梅生伟,孙元章.电力系统非线性控制[M].2版.北京:清华大学出版社,2008.

[5]李天云,高磊.基于HHT的电力系统的低频振荡分析[J].中国电机工程学报,2002(02).

[6]邓集祥,刘洪波.多机电力系统非线性振荡的研究[J].中国电机工程学报,2002(02).

[7]张鹏飞,薛禹胜,张肩平.电力系统时变振荡特性的小波脊分析[J].电力系统自动化,2004(16).

[8]王铁强,贺仁睦,徐东杰,等.Prony算法分析低频振荡的有效性研究[J].中国电机工程学报,2002,22(10):67-70.

[9]Hauer J F.Initial results in Prony analysis of power system response signals[J].IEEE Trans on Power System,1990,5(1):80-89.

[10]Hauer J F.Application of Prony analysis to the determination of modal content and equivalent models for measured power system reponse[J].IEEE Trans on Power Systems,1991,6(3):1062-1068.

[11]Trudnowski D J.Making Prony analysis more accurate using multiple signals[J].IEEE Trans on Power Systems,1999,14(1):226-231.

[12]Sanchez G J J,Chow J H.Performance comparison of three identification methods for the analysis of electromechanical oscillations[J].IEEE Trans on Power Systems,1999,14(3):995-1002.

[13]乐叶青,徐政.基于时频分布的电能质量交叉扰动检测[J].电力系统及其自动化学报,2007,19(6):114:-117.

[14]Ifeachor E C, Jerv is B W. Digital Signal Processing ,a Practical Approach[M].Boston,MA,USA:Addison-Wesley Longman Publishing Co.1993.

[15]Wright P S. Short-time fourier transforms and wignerville distributions applied to the calibration of power frequency harmonic analyzers [J].IEEE Trans on Instrumentation and Measurement,1999,48(2):475-478.

[16]ShieQian.Introduction to Time-Frequency and Wavelet Transforms [M].Prentice Hall,2001.