关于退化拟正则映射的加权不等式

刘倩倩，高红亚，展正然

(1.河北大学 工商学院，河北 保定 071000;2.河北大学 数学与计算机学院, 河北 保定 071000;3.中国地质大学 长城学院，河北 保定 071000)

关于退化拟正则映射的加权不等式

刘倩倩1，高红亚2，展正然3

(1.河北大学 工商学院，河北 保定 071000;2.河北大学 数学与计算机学院, 河北 保定 071000;3.中国地质大学 长城学院，河北 保定 071000)

为了研究退化拟正则映射的性质，将拟正则映射的加权Poincaré型不等式进行了推广.首先给出当权重为拟正则映射时的Poincaré型不等式和退化拟正则映射的概念，然后证明了当权重为退化拟正则映射时Poincaré型不等式仍然成立.

退化Jacobian行列式; 退化拟正则映射;Poincaré型不等式

近年来，许多学者在退化椭圆方程的基础上，建立了加权Poincaré型不等式.文献[1]证明了下面2 个不等式是等价的：

(1)

(2)

其中，1lt;plt;∞，ω(x)和v(x)-1/(p-1)是定义在A∞上的加权函数.文献[2]证明了在不等式(1)中，权ω和v不一定是定义在A∞上的函数，并证明了如果f∈W1,n(Ω,Rn)∩L∞是拟正则映射，令ω(x)=J(x,f),v(x)=J(x,f)1-(p/n)，1lt;plt;n，那么不等式(1)成立.本文是建立在文献[2]的基础上，证明了如果f∈W1,l(Ω,Rn)∩L∞是退化拟正则映射，令ω(x)=Jl(x,f)，v(x)=Jl(x,f)1-(p/l)，1lt;plt;l，那么同样有不等式(1)成立.

1 定义

退化拟正则映射的概念和性质被许多学者广泛研究[3-8]，退化拟正则映射的定义如下.

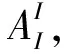
2)

|Df(x)|l≤KJl(x,f), a.e.Ω.

(3)

其中|Df(x)|是矩阵范数，|Df(x)|=sup|ξ|=1|Df(x)ξ|.

定义2 对于每一个方体Q及Q的任意一个可测子集E, 如果存在常数c,δgt; 0, 使得

成立，则称权ω(x)属于A∞类.

2 Poincaré型不等式

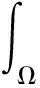
(4)

其中，c∈Rn是一个常向量.

证明

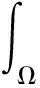
因为φ在Ω的边界为0, 得

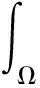
(5)

对于退化的拟正则映射f(x),由式(3)不难得|Df(x)|l-1≤K1-(1/l)Jl(x,f)1-(1/l)，令M=‖f‖∞，从式(5)中，得

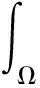
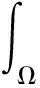
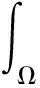
所以

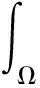
其中c=c(l,K,‖f‖∞).

[1] PÉREZ C.Two weighted norm inequalities for Riesz potentials and uniformLp-weighted Sobolev inequalities [J].Indiana Univ Math J, 1990, 39: 31-42.

[2] MOSCARIELLO G.Weighted Sobolev inequalities associated with quasiregular mappings [J].Nonlinearity, 1993, 6: 49-55.

[3] 郑神州, 方爱农.关于退化的拟正则映射[J].数学年刊, 1998, 19A(6): 741-748.

ZHENG Shenzhou, FANG Ainong.Degenerate quasiregular mappings [J].Chinese Annals of Mathematics,1998, 19A(6): 741-748.

[4] 高红亚, 吴泽民.退化拟正则映射的正则性[J].数学研究与评论, 2002, 22(4)：603-608.

GAO Hongya, WU Zemin.Regularity of degenerate weakly quasiregular mappings[J].Journal of Mathe-matical Research and Exposition, 2002, 22(4)：603-608.

[5] 高红亚.弱拟正则映射的若干性质[J].数学学报, 2002, 45(1):191-196.

GAO Hongya.Some properties of weakly quasiregular mappings[J].Acta Mathematica Sinica, 2002,45(1):191-196.

[6] 高红亚.弱(K1，K2)- 拟正则映射的正则性[J].中国科学, 2003, 33(1),:83-88.

GAO Hongya.Regularity of weakly(K1;K2)-quasiregular mappings[J].Science in China, 2003, 33(1),:83-88.

[7] 高红亚, 赵洪亮.保向形式Jacobian 行列式的可积性[J].中国科学, 2005, 35A(9): 1060-1070.

GAO Hongya, ZHAO Hongliang.Integrality of orientation Jacobian[J].Science in China, 2005, 35A(9):1060-1070.

[8] 高红亚, 顾广泽, 史明宇.退化弱拟正则映射的Caccioppoli 不等式[J].系统科学与数学, 2008，28(5):548-553.

GAO Hongya, GU Guangze, SHI Mingyu.Caccioppoli type inequality for degenerate weakly quasiregular mappings[J].Journal of Systems Science and Mathematical Sciences, 2008，28(5):548-553.

(责任编辑：王兰英)

Weighedpoincaréinequalitiesassociatedwithdegeneratequasiregularmappings

LIUQian-qian1，GAOHong-ya2,ZHANZheng-ran3

(1.Industrial and Commercial Collge, Hebei University, Baoding 071000, China； 2.College of Mathematics and Computer Science, Hebei University, Baoding 071002,China； 3.Great Wall College, China University of Geosciences, Baoding 071000,China)

In order to study the properties of degenerate quasiregular mappings, a weighed Poincaré type inequalities associated with quasiregular mappings is generalized.First the article gives the Poincaré type inequalities which weight is a quasiregular mapping and the definition of degenerate quasiregular mappings, then proves that the Poincaré type inequalities is still right when the weight is degenerate quasiregular mappings.

degenerate Jacobian; degenerate quasiregular mappings; Poincaré type inequality

O186.15

A

1000-1565(2012)01-0017-03

2010-11-28

国家自然科学基金资助项目(10971224) .

刘倩倩(1983-), 女，河北涞源人，河北大学助教，主要从事复分析和偏微分方程方向研究.

E-mail:lqq1688@163.com

高红亚(1969-), 男，河北顺平人，河北大学教授，主要从事复分析和偏微分方程方向研究.

E-mail:hongya-gao@sohu.com

MSC2010: 53C43