基于广义特征分解的盲信号分离算法

赵 艳，缪善林

(1.通信信息控制和安全技术重点实验室，浙江嘉兴 314033;2.中国电子科技集团第36研究所，浙江嘉兴 314033)

0 引言

盲信号分离是在信号源和传输信道完全或部分未知的情况下，只利用传感器阵列或天线阵列的观测数据来分离、提取源信号的信号处理理论。盲信号分离技术是近年来信号处理领域的一个研究热点，主要用于语音信号处理、图像信号处理、通信信号处理及地震信号处理等。C.Jutten等学者在20世纪80年代早期就针对盲信号分离引入了独立分量分析(ICA)技术，ICA技术包括极大似然估计方法［1］、最大熵方法、最小互信息方法、高阶累积量方法［2］、主分量分析(PCA)算法［3，4］、自然梯度算法［5～7］及 FastICA 算法［8，9］等。一般研究数学模型中，都假设源信号的数目和观测信号的数目相等，但实际电磁环境较为复杂，侦收到的源信号数目未知，即源信号数目可能比观测信号数目少或者多，且观测到的源信号频谱可能存在重叠的现象，这就给现有算法的应用带来了一定的局限性。对于源信号数目多于观测信号数目的盲信号分离，虽然已经提出了一些解决办法［10，11］，但在实际应用中效果并不理想，还有待进一步的研究。而当源信号数目少于观测信号数目时，常规方法认为只要所有的源信号至少被重构一次，即源信号可能被多次拷贝输出，则实现了对源信号的有效盲分离，但是若要真正地提取源信号，还需要已知源信号数目及相关的信号处理技术才能实现。针对常规盲分离方法存在的这些问题，给出了基于广义特征分解的盲信号分离方法，不需要知道信号数目就能够对源信号实施有效分离，所得的源信号不会被多次拷贝，并且在实际的应用中取得了较好的效果。

1 基本原理

假设有M个天线单元接收N个相互独立的入射信号(设为s1，s2，…，sN)，则天线阵列接收到的混叠信号可以表示为

式中，S=［s1，s2，…，sN］T;A 为 M ×N 列满秩混叠矩阵;X=［x1，x2，…，xM］T为各个天线单元接收到的信号;［·］T为矩阵转置。

为了得到各个输入信号，需要找到一个去混叠矩阵W，即

式中，Y=［y1，y2，…，yN］T为 S 的估计矩阵。因此，Y中的任意一个元素y都可以认为是N个输入信号的线性混叠信号，即

式中，q=［q1，q2，…，qN］T是 N 维非零向量。

假设存在一个函数f使得f(si)(i=1，2，…，N)之间互不相关，且满足式(4)和(5)

式中，cov(y)非零;cov(·)为求解协方差。则定义

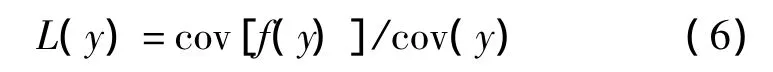
由于S及f(S)都是由非相关信号组成的，其中 f(S)=［f(s1)，f(s2)，…，f(sN)］T，则存在以下关系

式中，diag［·］为对角阵。于是

即有

根据式(7)可以得到

另外，根据式(3)可以得到

根据前面的分析可以得到

式中，L(sm)=max{L(s1)，…，L(sN)}，则有

当且仅当y=asm时，式(13)等号才能成立。因此，可以根据下面的连续函数获得信号sm的最优求解

式中，y=wX(w为W的某一行向量)。恢复sm后即可恢复出其他信号，并最终获得解混叠矩阵W。

2 基于广义特征分解的求解方法

由于 L(s1)，L(s2)，…，L(sN)相互不相等，假设

根据前面的分析可以得到

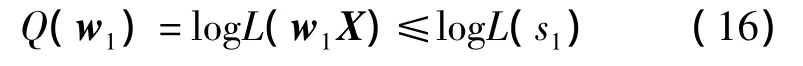
即

式中，wGOP为w1的最优求解。为了获得wGOP，根据Q(w1)的梯度计算可得

令▽Q(w1)=0可得

则利用广义特征分解即可获得w1。

在实际计算中，需要将原始接收数据X进行中心化及白化处理，中心化处理即将接收数据X变为均值为0的信号为

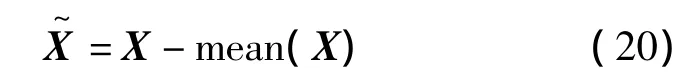
式中，mean(·)为取均值。同时，为了将中心化处理后的信号进行白化处理，需要对信号进行特征值分解，即

式中，E表示特征向量;D表示特征值。

白化信号可以表示为

根据式(19)～(22)即可获得混合前的信号。

3 实验结果

实验1:实验采用的输入信号样式如式(23)表示，其混叠矩阵采用如式(24)所示。混合前的3个原始信号如图1所示，混合后的3路接收信号如图2 所示，分离后的3个信号如图3所示。

实验2:某系统接收天线是由5单元天线组成的均匀圆阵，接收来自远处的2个信号，信号1的频率为2 209.075 MHz和码速率为9.6 ksps的 QPSK信号，信号2的频率为2 209.045 MHz和码速率为19.2 ksps的BPSK信号，则分离前后信号的频谱如图4所示。

图4 分离前后信号频谱图

根据分离后的信号进行参数估计，结果见表1，分离后的两个信号解调结果，如图5和图6所示。

表1 分离信号参数估计

实验3:采用实验2的系统，接收来自远处的两个信号，信号1的频率为2 209.075 MHz和码速率为24.8 ksps的QPSK信号，信号2的频率为2 209.045 MHz和码速率为19.2 ksps的BPSK信号，经过多普勒频率漂移之后，频谱有所重叠，本文盲分离方法与常用的FastICA方法及自然梯度方法的分析处理结果，如图7～图9所示。其中，每幅图中的第一个为观测信号的频谱图，第二个至第六个为五个分离后的估计信号的频谱图。

通过实验验证可以看出，利用盲分离方法，输出的估计信号中不存在源信号多次拷贝的问题，在源信号数目未知的情况下即可实现对频率相隔很近的源信号进行有效分离，与常规方法相比具有更好的分离效果。

4 结语

针对当前复杂的电磁环境，给出了一种基于广义特征值分解的盲信号分离方法，该方法无需进行迭代运算即可实现盲信号分离，从而降低了计算的复杂度，且对信号的适应性具有较好的效果，通过实验验证了该方法的有效性。

［1］LIN S L，TUNG P C.Application of Modified ICA to Secure Communication in Chaotic Systems［C］//Lecture Notes In Computer Science，2007(4707):431-444.

［2］TAOUFIKI M，ADIB A，ABOUTAJDINE D.Blind Separation of Any Source Distributions via High-Order Statistics［J］.Signal Processing，2007，87(8):1 882-1 889.

［3］吕齐，朱孝龙，张贤达.卷积盲信号分离的非线性PCA方法［J］.清华大学学报(自然科学版)，2006，46(4):492-494.

［4］马丽艳，李宏伟.一种基于非线性PCA的卷积混合盲源分离算法［J］.电子学报，2008，36(5):1 009-1 012.

［5］付卫红，杨小牛，曾兴雯，等.适用于通信侦察的信号盲分离算法［J］.南京理工大学学报:自然科学版，2008，32(2):189-194.

［6］CICHOCKI A，UNBEHAUEN R.Robust Neural Networks with On-line Learning for Blind Identification and Blind Separation of Sources［J］.IEEE Trans.Circuits and Systems I:Fundamentals Theory and Application，1996，43(11):894-906.

［7］AMARI S，CICHOCKI A，YANG H H.A New Learning Algorithm for Blind Signal Separation［C］//Advances in Neural Information Processing Systems，Canbrige，Ma:MIT Press，1995，8:757-763.

［8］郭武，朱长仁，王润生.一种改进的FastICA算法及其应用［J］.计算机应用，2008，28(4):960-962.

［9］贾银洁，许鹏飞.基于FastICA的混合音频信号盲分离［J］.信息与电子工程，2009，7(4):321-325.

［10］T-W LEE.Independent Component Analysis-Theory and Application［M］.Holland:Kluwer，1998.

［11］GIROLAMI M.Advances in Independent Component Analysis［M］.Berlin:SpringerVerlag，2000.