基于多体系统理论的丝杠热误差补偿系统的研究

岳红新,石 岩,李国芹

(河北工程技术高等专科学校 电力工程系,河北 沧州 061001)

机床在加工过程中,热误差是由于温度上升引起机床元件的膨胀变形并最终导致工件和刀具之间的相对位移而引起的加工误差。大量研究表明,在精密加工中,由机床热变形所引起制造误差占总误差的40%～70%[1]。由于热误差具有非线性变化、非正态不平稳分布和多因素交互作用的特性[2-3],采用拟合建模方法来精确建立热误差数学模型具有相当的局限性。

数控机床向高速高精方向的发展对滚珠丝杠的精度提出了更高的要求。研究滚珠丝杠的温升及热变形规律对提高机床的加工精度具有重要意义。丝杠的热变形是一个复杂的非线性时变系统,受到诸多因素的影响,要建立它的数学模型是非常困难的,即使能够建立,求解起来也是非常复杂的。本研究指出了基于多体理论提出了热误差建模的理论和方法,利用神经网络获取热变形参数,计算并补偿热变形误差。

1 基于多体系统的综合热误差模型的建立

多体系统[4]是对一般复杂机械系统的完整抽象和有效描述,它是分析和研究复杂机械系统的最优模式。多体系统误差运动分析的其基本原理是用低序体阵列方法描述多体系统拓扑结构的关联关系,在多体系统拓扑结构上建立广义坐标系,用齐次列阵表示点和矢量,用 4*4阶齐次方阵描述点在广义坐标系中的变换关系,使有误差多体系统的运动分析变得简单、迅速、明了和普遍适用[5]。

1.1 加工中心拓扑结构描述

三轴立式加工中心是较简单的多体系统,图 1为MAKINO三轴加工中心的结构示意图。建模前先给系统中的各体编号,其拓扑结构见图2。从图中可以明显看出,该加工中心拓扑结构包括刀具分支和工件分支,刀具分支为惯性参考坐标系,工件分支为惯性坐标系。

对于任意多体系统,都可用低序体阵列对已定义的拓扑结构进行数字化描述。低序体阵列中,各体通过相连接体按照序号从大到小的原则最终达到惯性参考坐标系。图2中多体系统的拓扑结构可用表1所示的低序体阵列来描述。

图1 立式加工中心结构示意图

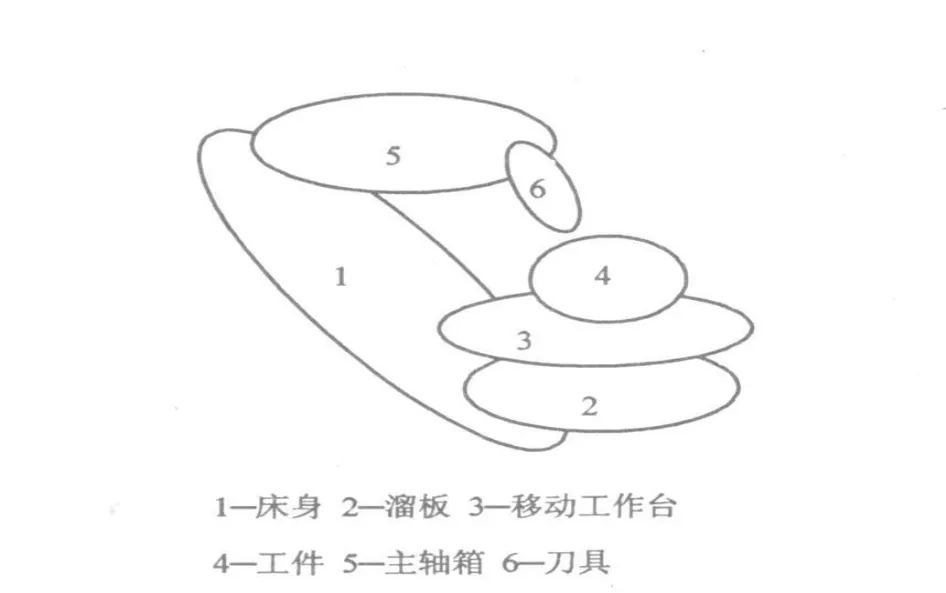
图2 立式加工中心拓扑结构

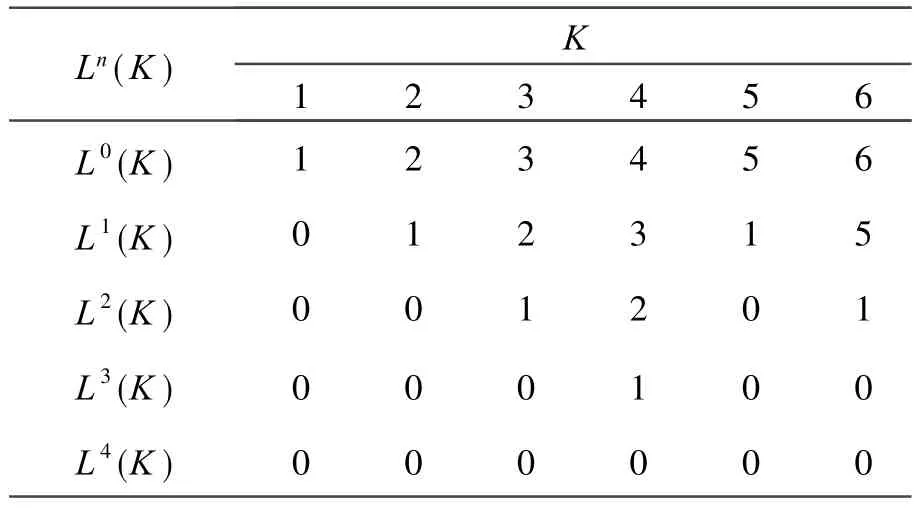
表1 立式加工中心低序体阵列

1.2 相邻体间坐标变换矩阵

基于多体系统理论,其相邻体间变换矩阵为

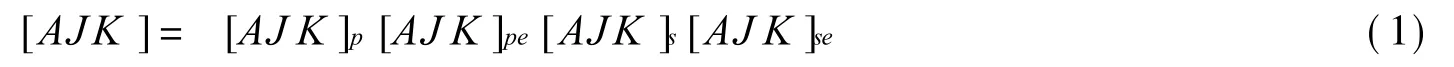
式中,[AJK]p和[AJK]s为坐标系特征矩阵;[AJK]pe和[AJK]se为典型体位置误差和运动误差变换矩阵[5]。 其中

在床身-工件分支中,2体的实际运动参考坐标系相对于理想运动参考坐标系沿Y向平移一个d2py;3体的实际运动参考坐标系相对于2体的体坐标系沿x向平移一个d3py,并转过垂直度误差e3pz,最终平行于X轴。

在床身-测头分支中,主轴箱 5的实际运动参考坐标系相对于理想运动参考坐标系沿Z向平移一个矢量d5pz,并转过垂直度误差e5px和e5py,最终平行于Z轴;测头6的实际运动参考坐标系与理想运动参考坐标系之间存在的位置误差有d6px,d6yp,d6pz,e6px,e6yp和e6pz。

1.3 热误差模型的建立

设刀具在刀具体坐标系中的位置矢径为[t6]=[0,0,-h]T,理论加工点在工件坐标系中的位置矢径为= [w4]= [xw,yw,zw]T。

令etw表示刀具和理论加工点的矢量偏差,则

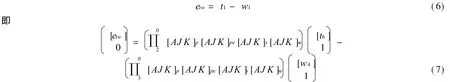
与几何模型相比,热误差模型中多了几项由机床热变形引起的位置误差,并且其中的位置误差和运动误差参数都随温度场的变化而变化。包括刀具实际运动参考坐标系相对于理想运动参考坐标系的六项位置误差W6px,W6py,W6pz,X6px,X6py和X6pz;x轴丝杠的热变形误差W3sx,W3sy,W3sz,X3sx,X3sy,X3sz;y轴丝杠的热变形误差W2sx,W2sy,W2sz,X2sx,X2sy,X2sz;z轴丝杠的热变形误差W5sx,W5sy,W5sz,X5sx,X5sy,X5sz。

在W6px,W6py,W6pz,X6px,X6py和X6pz六项热误差参数中,由于X6pz对加工无影响,因此此取值为零。实验发现W6px,X6py,X6pz引起的误差量很小,可以忽略[6]。W6py和W6pz用多元线性回归方法进行辨识[7]。

2 基于神经网络的丝杠热误差参数辨识

径向基函数神经网络的结构为3层,第 1层是输入层,由信号源节点组成;第 2层为隐含层,神经元个数由所描述的问题确定,神经元的变换函数是中心点径向对称且衰减的非负非线性函数;第 3层为输出层,可对输入模式做出响应。

在丝杠的热误差模型中,网络的输入为某时刻测温点的温升变化,输出为该时刻对应的热误差参数值,变换函数为高斯函数。在每轴丝杠的轴承处作为测量点,同时在丝杠上每隔 100 mm设置一个测点,15个测量点用于测量丝杠不同位置处的温度变化情况。采用 HP10754A双频激光干涉仪测量丝杠的热变形[8]。

3 实验结果

将实验样件设计为两排小凸台,如图 5所示。一排用于无补偿的加工,一排用于带热补偿的加工;分两天进行加工,加工后在三坐标测量机上检测并比较结果,进而验证热误差补偿模型的补偿效果。

从凸台各侧面上的补偿效果看,X侧面的加工精度平均提高72.98%,Y侧面的加工精度平均提高78.39%,Z侧面的加工精度平均提高86.27%;从整体补偿效果来看,经补偿加工凸台的尺寸精度平均提高了79.21%。

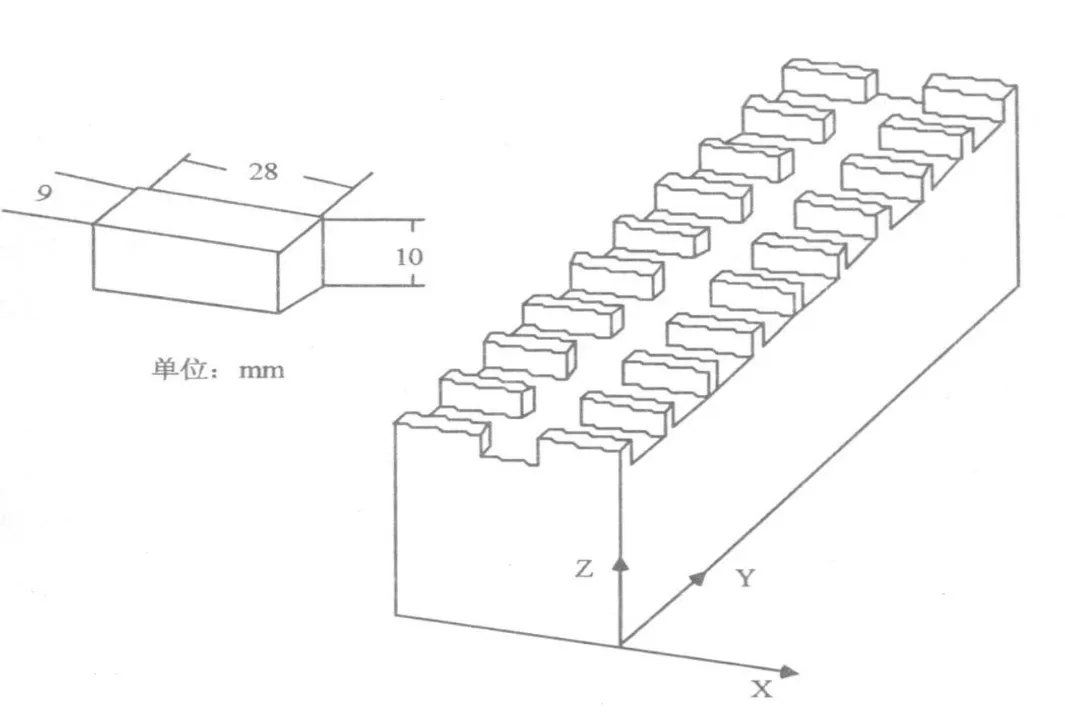
图5 实验样件及在工作台上的安放位置

4 结论

采用多体系统理论方法建立了能对丝杠的热误差进行补偿的综合模型。其中对X、Y、Z轴的W2sy,W3sx,W5sz热误差参数的辨识运用神经网络的方法。通过理论分析和建模举例可以看出,该方法简单明了,不受机械结构、运动复杂程度的限制,具有广泛的通用性,可用于实时补偿。

[1]鲁远栋,徐中行,刘立新,等.数控机床热变形误差补偿技术 [J].机床与液压,2007,35(2):43-45.

[2]郭前建,杨建国,李永祥,等.滚齿机热误差补偿技术研究[J].中国机械工程,2007,18(23):281-282.

[3]Pahk H J,Lee S W.Thermal Error Measurement and Real Time Compensation System for the CN Machine Tools.Incorporating the Spindle Thermal Error and the Feed Axis Thermal Error[J].International Journal of Advanced Manufacture Technology,2002,20(7):487-494.

[4]刘又午.多体动力学的休斯敦方法及其发展 [J].中国机械工程,2000,11(6):601-607.

[5]粟时平,李圣怡.五轴数控机床综合空间误差的多体系统运动学建模 [J].组合机床与自动化加工技术.2003(5):15-21.

[6]张志飞.多轴数控机床热误差与几何误差建模及补偿技术的研究[D].天津大学,2001.

[7]章青,岳红新,王慧清.四轴加工中心热误差建模及补偿技术研究 [J].制造技术与机床,2004(10):55-58.

[8]岳红新,章青,潘平平.基于RBF神经网络的丝杠热误差模型研究 [J].机械设计与制造,2011(2):128-129.