多效蒸发工程中最佳效数的计算

胡柏松，杨玉梅，赵景利

（1.河北工业大学化工学院，天津300130；2.中海油天津化工研究设计院）

化工装备与设计

多效蒸发工程中最佳效数的计算

胡柏松1，杨玉梅2，赵景利1

（1.河北工业大学化工学院，天津300130；2.中海油天津化工研究设计院）

无机盐行业中涉及到溶液浓缩问题，一般均采用多效蒸发工艺。多效蒸发能够节约蒸汽消耗，但随效数增加设备投资也相应增大。由于多效受到设备投资和折旧费以及传热温差的限制，效数不可能无限增大。当设备投资费用不抵节能费用时，再增加效数已毫无意义。在选择最佳经济效数时，由于变量较多，故存在一定难度。将最佳效数与年消耗最低费用关联起来，建立一个年费用目标函数式，提出了最佳效数的简易公式。通过工程实际验证，该公式简便、可行、可靠。

多效；蒸发；最佳效数；年消耗最低费用

在无机盐行业中，碳酸钾、氯化铵、硝酸钾、硫酸钠等溶液的浓缩过程一般采用蒸发操作。由于该工序能耗较大，故在蒸发工程设计时，应尽量确保蒸发装置在低能耗和低投资的前提下高速度、高效率运行，也就是使蒸发装置取得最佳的经济效益［1］。实际操作中，一般采用多效蒸发工艺，但是节能效益直接由设备投资决定。效数越多，节能效果越好。而效数受两方面因素限制［2］：1）设备投资与设备折旧费。设备投资几乎与效数成正比关系，而节能的能耗却与其成反比。当节约出的能源费用不足以补偿设备折旧增加的费用时，再增加效数就失去经济价值。2）传热温差。首效的加热蒸汽温度和末效的真空度确定后，整套装置的总传热温差是一定的。效数越多，分配到各效的传热温差就越小，再加上各效的温差损失之和要大于单效蒸发的温差损失，使得各效蒸发的有效传热温差变小，即多效蒸发装置的生产能力变小了。由于上述两方面原因限制了效数的增加，所以最佳效数的经济性设计与计算成为多效蒸发设计的首要工作。

1 最佳效数目标函数的建立

为简化计算，优化设计中最好在目标函数中只设一个变量［3］，则单变量的优化成为“一维搜集”问题，即可用一元函数的微分求极值法进行优化。

在确定最佳效数时，首先建立一个目标函数，该函数以年蒸发总费用最小为目标。因此，在蒸发规模一定的前提下，设定年费用目标函数为Cr（x），寻求该函数的最小值。设最佳效数的目标函数Cr（x）由基本投资的年折旧费用F（x）与年蒸发单位消耗费用E（x）两个单变量方程组成，即：

上式中基本投资的年折旧费用F（x）与效数呈线性增大关系，即：

式中，j为设备市场变化系数（当年设计、当年施工j=1）；b为价格常数；a为单效蒸发器每蒸发1 t水的折旧费，元/t，可按下式计算：折旧费（a）=（基本投资/设备寿命+年大修费用）/年蒸发量［2］。基本投资按照文献［4］投资估算中“系数连乘法”求得，即基本投资为设备投资的2.245倍；年大修费用为每年投资的5%～10%。表1为蒸发消耗量和效数之间的关系［2］。

表1 多效蒸发蒸汽消耗与效数关系 kg/kg

由表1可以看出，单位蒸汽消耗E′（x）随着效数（x）增加逐渐下降，将表1数据回归，得如下方程：

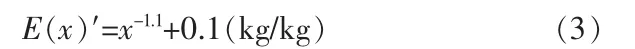
则单位消耗费用方程：

式中，M为蒸汽价格，元/t；k为蒸汽市场变化系数，随时间和地点而变（当地、当时k=1.0）。

将式（2）、（4）带入式（1）中得到总目标函数方程：

该函数为连续的，可微的。按照文献［5］函数求极值的办法，对函数进行求导。欲使目标函数Cr（x）有极值，则令：

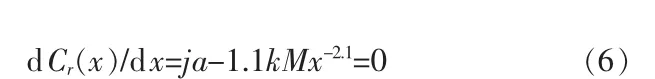
再对该函数进行二次求导：

其中k、M均为正值，因此dCr2（x）/dx2＞0。说明该目标函数有极小值。即当效数取最佳效数时年费用最小。由式（6）可得最佳效数计算方程式如下：

由式（8）分析可知，只要知道当地蒸汽价格和单效蒸发器每蒸发1t水的折旧费，即可快速算出最佳效数。

2 设计计算

某工厂处理氯化铵溶液，原始含量为10%（质量分数），处理量为10 t/h，采用多效蒸发工艺，试确定蒸发工程最佳效数。

2.1 计算过程

①总蒸水量：W=10×（1-10%)=9 t/h；②设定每年工作时间为7 200 h，全年蒸水量：W年=9×7 200＝6.48万t/a；③采用全钛蒸发器，按换热面积4 500元/m2，需要换热总面积530 m2，蒸发器费用4 500×530=238.5万元，其他辅助设备占蒸发器的20%，故整套装置费用：238.5×1.2=286.2万元；④设备设计使用寿命为10 a，设备折旧按平均分摊法，因为氯化铵溶液腐蚀性很强，故年大修费为10%；⑤蒸发每吨水的折旧费：a=[（2.245×286.2/10）×1.1]/ 6.48=10.9元/t；⑥蒸汽价格：150元/t，价格变动指数：j=1，k=1，最佳效数：x=（1.1kM/ja）0.476=（1.1×150/10.9）0.476=3.6。

2.2 与工程实际比较

河北、浙江、山东等某些厂处理含氯化铵工业废水，设计时采用三效加热泵蒸发，实际节能效数为3.5～3.8，运行效果良好。最佳效数的计算公式得到的结果与实际工程设计吻合较好。

3 结论

在多效蒸发工程设计的初始阶段，在确定效数时，未知变量较多，所以确定效数有一定的难度。研究将最佳效数与年消耗费用最小关联起来，建立效数与年消耗费用的函数方程。利用函数极值求法，得到了多效蒸发的单位消耗费用方程。通过该方程可知，只要掌握蒸汽价格和每蒸发1 t水的基本投资折旧费，即可简便地计算出最佳效数，通过工程实例验证，该方程简便、可行、可靠。

［1］史晓平，胡建勋，刘常松，等.复分解法生产小苏打母液的综合处理［J］.无机盐工业，2010，42（8）：57-59.

［2］时钧.化学工程手册.［M］.北京：化学工业出版社：2002.

［3］盛展武.化工装置经济［M］.北京：化学工业出版社，1998：134-135.

［4］黄振仁.过程装备成套技术［M］.2版.北京：化学工业出版社，2008：24-26.

［5］同济大学数学系.高等数学［M］.6版.北京：高等教育出版社，

2007.

Research on calculation of optimum evaporator numbers in multi-effect evaporation system

Hu Baisong1，Yang Yumei2，Zhao Jingli1
（1.School of Chemical Engineering and Technology，Hebei University of Technology，Tianjin 300130，China；2.CNOOC Tianjin Chemical Research&Design Institute）

Generally，the concentration of solutions in inorganic salt industry all adopts multi-effect evaporation method.The steam consumption can be saved by multi-effect evaporation system，but equipment investment will be raised as the increasing of the effect number.The effect number is limited by equipment investment，depreciation cost，and heat transfer temperature difference，so the infinite increase of effect is impossible.When the equipment investment is more than the energy saving，adding effect number is meaningless.The question of selecting the best effect number was very important.Because there are many variables，the selection was very difficult.Correlation between the best effect number and annual minimum cost of consumption was linked,a function for annual cost goal was established and a simple formula for the best effect number was proposed.According to the actual engineering，the formula was simple，feasible，and reliable.

multi-effect；evaporation；the best effect number；annual minimum cost of consumption

TQ051.62

A

1006-4990（2012）11-0055-02

2012-05-19

胡柏松（1981— ），男，实验师，硕士，主要研究方向为蒸发技术与装置的研发、推广，废水处理等工作，已公开发表文章8篇。

联系方式：hubaisong@163.com