磁传感器阵列布置形式对铁磁目标磁场信息量获取的影响

张安明 虞伟乔 郭成豹

1 海军驻大连船舶重工集团有限公司军事代表室，辽宁大连 116005 2 中国人民解放军91656部队，上海 200231 3 海军工程大学 电气与信息工程学院，湖北 武汉 430033

1 引 言

由于目前对复杂铁磁目标的磁性变化过程还不是很了解，因此即使是拥有完整的磁性历史信息，也很难用精确的数学模型去描述这些复杂的物理过程。为了对铁磁目标的磁场进行精确建模，有必要利用磁传感器测量铁磁目标周围特定区域的磁场分布，以根据测量数据重建铁磁目标的磁源分布。类似这样的应用包括：磁特征分析、无损检测、电流测量以及生物磁学应用等。在实际应用中，所面临的一个重要问题是磁传感器的布置位置和需要布置的数量，特别是需在现存或预定义的磁传感器组合阵列中进行对比选择。其中，最关键的就是要建立一种合适的评价标准，以对这些阵列形式的优劣程度进行评估。

本文将采用观测矩阵的奇异值坡度作为评价标准，对理想布置和简化布置形式下的磁传感器三分量阵列和垂直分量阵列进行对比分析和评估，发现简化三分量阵列是实际工程中最可取的阵列形式。

2 铁磁目标磁场信息获取量评估方法

可将铁磁目标的磁场测量和建模问题描述为下述方程：

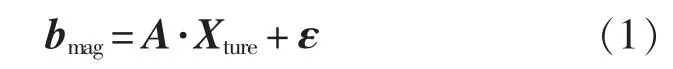
式中，bmag为具有m个磁场分量测量值的列向量；A（m×n）为观测矩阵；Xture为源分布，被表示为一个长度为n的列向量；ε为列向量，表示噪声。

在线性逆问题中，不确定性的一种相关来源是测量系统的不精确性 （如传感器方位或位置变化），这些不精确性会影响到观测矩阵A。在本文的分析中没有考虑这种影响，因为在铁磁目标反演建模中，这种影响所占的比重较小，通常这些问题呈现出超定 （即测量数据的数目大于未知参数数目）和病态的特点。问题的求解通常采用基于奇异值分解的正则化方法，如截断奇异值分解法（TSVD）［1-4］。

观测矩阵的条件数常被作为一种典型的评价标准，但基于条件数的分析却受限于这样的事实：病态逆问题的解是由正则化算法获得，而正则化算法中所采用矩阵的条件数与观测矩阵的条件数又不同。此外，观测矩阵的条件数等于最大奇异值与最小奇异值之间的比值，而未考虑到其它奇异值的作用。因此，本文采用奇异值坡度作为评价标准，对铁磁性目标磁场反演建模所采用的阵列形式进行对比分析。

为了得到观测矩阵A，可以针对铁磁目标磁性磁场模型采用正演计算技术，本文采用了积分方程法［5-9］。本文的模型是基于一个虚拟铁磁船舶的主船体结构（图1），长100m，宽10m，将其划分为44个铁磁薄板单元。

观测矩阵A是病态的，且通常为非对称。由于奇异值分解 （SVD）能够处理非对称和奇异矩阵，因而观测矩阵A可表达为：

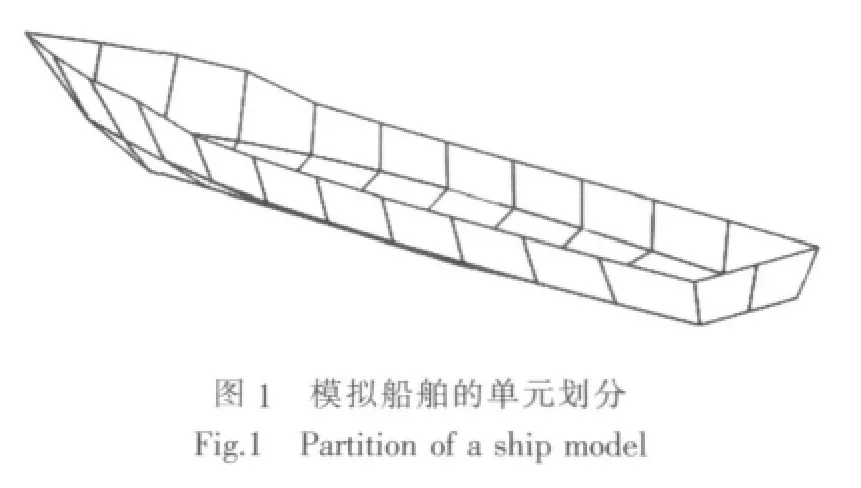
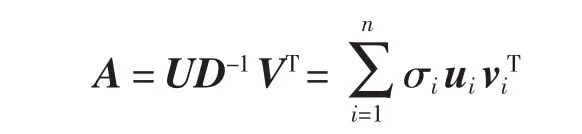
式中，U＝（u1，…，um），V＝（v1，…，vn）为正交矩阵；D＝diag（σ1，σ2，…，σn），为 A 的奇异值矩阵，降序排列。

式（1）的最小二乘解可表示为：

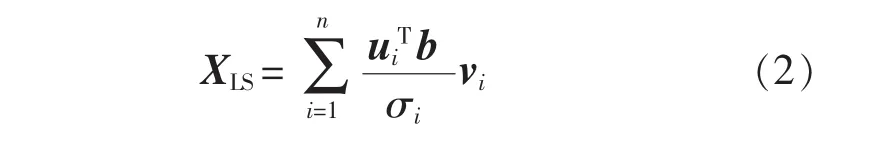
当将观测值b表示为真值与噪声之和时，有b＝bt＋e，其中bt为真值，e为噪声，从而可得式（2）的分解式为：

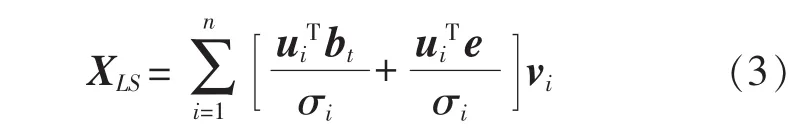
分析式（3）可知，噪声对真解的污染主要反映在右式第2项，特别是当奇异值σi异常小时，该污染项的值很大，甚至掩盖了反映真解的右式第1项，这样得到的解是没有意义的。

为避免小奇异值导致的虚假解，可以采用被称为正则化的特殊滤波技术，如截断奇异值分解法（TSVD），TSVD法可将容易造成不稳定的较小奇异值直接截去。对式（2）和式（3）进行修改：

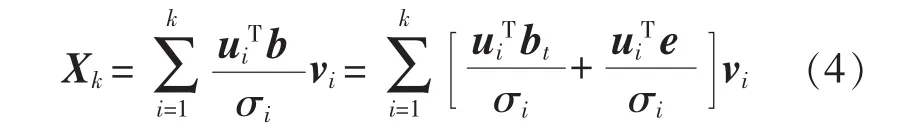
再适当去除（n-k）个大污染项，其虽然恢复了一些解的主要特性，但同时也丧失了一些解的精确性。整数k是截断参数，同时也是正则化参数。

由此可见，在使用正则化方法求解静磁逆问题的过程中，为了得到有效解，只保留了前k个奇异值，并得到了TSVD正则化解。TSVD的截断点k的合理选择取决于数据中的噪声水平，可以按照不同的准则进行判断。因此，在不同结构的磁传感器阵列中进行选择时，以观测矩阵条件数作为评价标准的分析方法已不适用，而本文所采用的将奇异值的坡度作为观测矩阵病态程度的评价标准则可得到更全面、深入的认识。

本文拟将奇异值坡度分析法［10］用于铁磁目标的反演建模问题。首先，采用一种理想的磁传感器阵列作为测量系统，并对上述铁磁船舶模型进行磁场测量，以作为参考标准。然后，构建几种常见的磁传感器阵列形式，并与上述参考标准进行对比分析，从而得到一些有意义的结果。

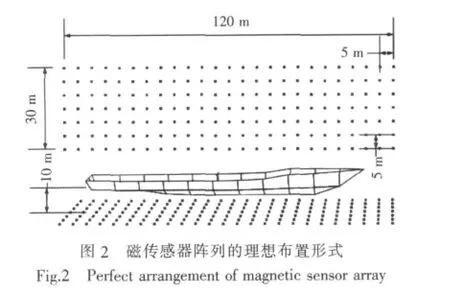
为收集足够的船舶磁场信息，设置了25×7＝175个三分量磁传感器，均匀分布于船舶下方的大平面上（图2），并测量船舶磁场的三分量。船舶中心点位于测磁平面中心的正上方，测磁平面的展布范围为横向［-15m，＋15 m］，纵向［-60m，＋60 m］，磁场测量点横向与纵向间的间隔均为5 m。若利用三分量磁场测量结果，可以形成的线性方程组具有44×2＝88个未知数 （各个单元的磁化强度分量），175×3＝525个方程 （此时称为理想三分量阵列）；若利用垂直分量磁场测量结果，则有175×1＝175个方程 （此时称为理想垂直分量阵列）。

为减少传感器数目，对磁传感器阵列进行了简化（图3）。此时的磁场测量结果可以形成的线性方程组具有44×2＝88个未知数 （各个单元的磁化强度分量），65×3＝195个方程（此时称为简化三分量阵列）。若利用垂直分量磁场测量结果，则有65×1＝65个方程 （此时称为简化垂直分量阵列）。

3 计算结果分析

本文对上述理想三分量阵列、理想垂直分量阵列、简化三分量阵列和简化垂直分量阵列这4种情况所对应的观测矩阵进行了计算，然后，又分别进行了奇异值分解计算，得到了相应的奇异值分布，如图4所示，图中的奇异值分布根据各自的最大值分别进行了归一化处理。

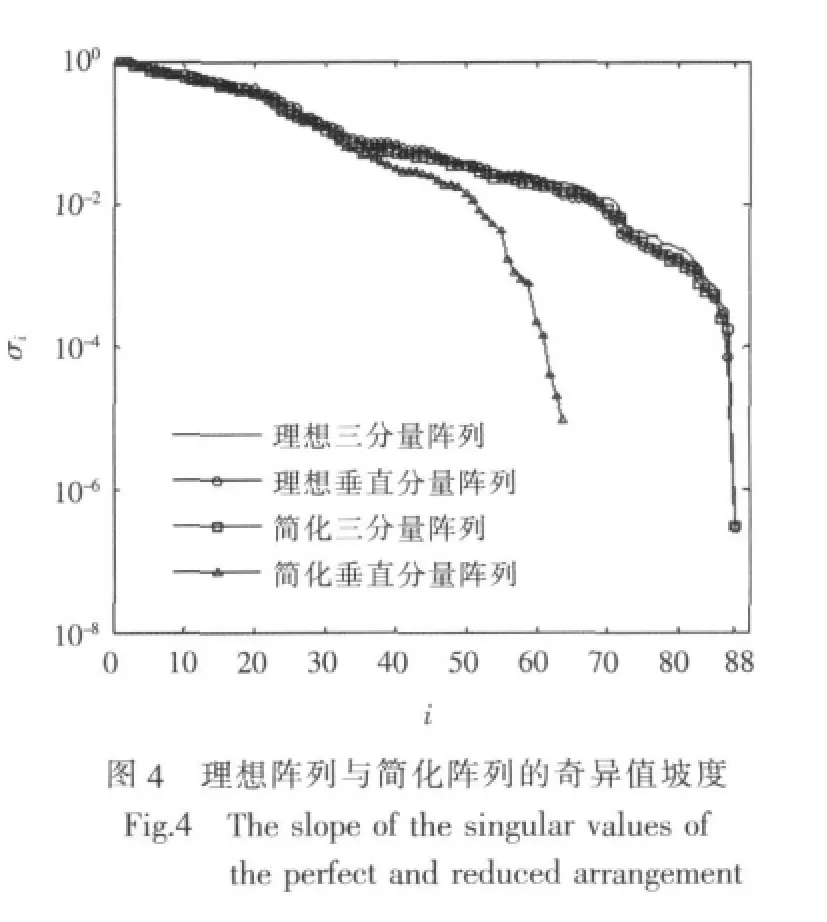
图4中所示的奇异值坡度表明，船舶磁场反演建模问题是病态的，其中，理想三分量阵列可以得到最小的奇异值坡度，理想垂直分量阵列和简化三分量阵列得到的奇异值坡度与理想三分量阵列相比稍大，简化垂直分量阵列得到的奇异值坡度最大。由此，可得出以下结论：

1）在理想阵列情况下，即测磁阵列分布范围足够广、磁传感器分布最稠密的情况下，进行三分量磁场测量和垂直磁场测量所得到的磁场信息均较多，这两种测磁阵列的效能相差不大。

2）在简化阵列情况下，即测磁阵列分布范围不够广、磁传感器分布不够稠密的情况下，进行三分量磁场测量比进行垂直磁场测量所得的磁场信息多，这两种测磁阵列的效能相差较大。

3）与垂直磁场测量相比，三分量磁场测量能得到更多的磁场信息。理想垂直分量阵列采用的是175个测磁通道，简化三分量阵列采用的是65×3＝195个测磁通道，二者采用的测磁通道数目相近，几乎得到了同样多的磁场信息（由图4可看出，理想垂直分量阵列与简化三分量阵列所得到的奇异值坡度非常接近）。

4 结 论

本文以奇异值坡度为评价标准，进行了理想测磁阵列和简化测磁阵列的对比分析。结果表明，在实际应用中，简化三分量阵列是最可取的阵列形式，因为这种阵列既能获得较多的磁场信息，又能减少测量点数，且占地也最小，若综合考虑场地、投资以及施工便利性等因素，简化三分量测磁阵列的优势将更加显著。

［1］杨文采.地球物理反演的理论和方法［M］.北京：地质出版社，1989.

［2］李卫兵，陈剑，毕传兴，等.联合波叠加法的全息理论与实验研究［J］.物理学报，2006，55（3）：1264-1270.LI W B，CHEN J，BI C X，et al.Investigation on holographic algorithm and experiment of combined wave superposition approach［J］.Acta Physica Sinica，2006，55（3）：1264-1270.

［3］毕传兴，陈心昭，陈剑.半自由声场的全息重建和预测实验研究［J］.物理学报，2004，53（12）：4268-4276.BI C X，CHEN X Z，CHEN J.Experimental study on the holographic reconstruction and prediction of semi-free field［J］.Acta Physica Sinica，2004，53（12）：4268-4276.

［4］黄群星，刘冬，王飞，等.基于截断奇异值分解的三维火焰温度场重建研究［J］.物理学报，2007，56（11）：6742-6748.HUANG Q X，LIU D，WANG F，et al.Study on threedimensional flame temperature distribution reconstruction based on truncated singular value decomposition［J］.Acta Physica Sinica，2007，56（11）：6742-6748.

［5］郭成豹，肖昌汉，刘大明.基于积分方程法和奇异值分解的磁性目标磁场延拓技术研究［J］.物理学报，2008，57（7）：4182-4188.GUO C B，XIAO C H，LIU D M.Research on continuations of magnetic object based on integral equation method and singular value decomposition［J］.Acta Physica Sinica，2008，57（7）：4182-4188.

［6］CHADEBEC O，COULOMB J.Magnetization identification problem illustration of an effective approach［J］.COMPEL：The International Journal for Computation and Mathematics in Electrical and Electronic Engineering，2004，23（2）：518-530.

［7］CHADEBEC O，COULOMB J，LECONTE V.Modeling of static magnetic anomaly created by iron plates［J］.Transactions on Magnetics，2000，36（4）：667-671.

［8］IGARASHI H，HONMA T，KOST A.Inverse inference of magnetization distribution in cylindrical permanent magnets［J］.Transactions on Magnetics，2000，36（4）：1168-1171.

［9］ESKOLA L，PURANEN R，SOININEN H.Measurement of magnetic properties of steel sheets［J］.Geophysical Prospecting，1999，47（4）：593-602.

［10］NALBACH M，DÖSSEL O.Comparison of sensor arrangements of MCG and ECG with respect to information content［J］.Physica C：Superconductivity，2002，372/376：254-258.