舱壁打孔的环肋圆柱壳振动性能分析

黄振卫 周其斗 纪 刚 王路才 刘文玺

海军工程大学船舶与动力学院，湖北武汉 430033

1 引 言

在潜艇舱段的实际结构中，由于主机轴承和鱼雷发射管的安装要求，往往需要在舱壁上布置圆形孔，从而导致舱壁结构发生变化。因此，研究因舱壁出现圆形孔所导致的潜艇振动性能变化，对潜艇振动优化设计具有重要意义。

带肋圆柱壳作为潜艇的典型结构形式，近年来对它的研究越来越多［1-3］。 曾革委等［4］借助线弹性理论，建立了加肋圆柱壳声辐射计算模型，通过大量数值计算，研究了舱壁、环肋刚度与间距以及结构阻尼等因素对辐射声压的影响。陈美霞等［5］研究了不同激励力对流场中敷设阻尼材料的有限长加筋双层圆柱壳的振动和声辐射性能的影响。谢志勇等［6］采用结构有限元和内域流体有限元的流固耦合计算方法，对加筋双层圆柱壳的固有频率和振型进行了计算，并与试验结果进行了对比。艾海峰等［7］研究了通过增加双层加肋圆柱壳的刚度降低低频噪声。王路才等［8］采用结构有限元耦合流体边界元的附加质量附加阻尼算法，讨论了以舱段模型代替整艇模型进行噪声估算的可行性。白雪飞等［9］以出现较大损伤变形的环肋圆柱壳为研究对象，计算了这种结构在静水外压作用下的应力分布和失稳临界压力。但以上研究都是针对严格按照设计制作的舱壁完整结构展开的，而实际制作的结构由于设备安装的要求，在舱壁上需要布置一定数量和大小的圆形孔，对由此带来的整个结构振动性能的变化规律的研究，目前仍处于起步阶段。

本文将运用PATRAN建立结构有限元模型，计算结构在不考虑开孔加强结构的条件下，改变圆形孔的大小、位置、数量以及含圆形孔的舱壁数量时的均方法向速度级，并对数值计算结果进行初步的比较和分析，从而得到舱壁开孔对环肋圆柱壳真空中振动性能的影响。

2 结构有限元算法

用有限元对模型进行有限元离散，并考虑稳态响应问题，可以得到：

3 环肋圆柱壳振动模型

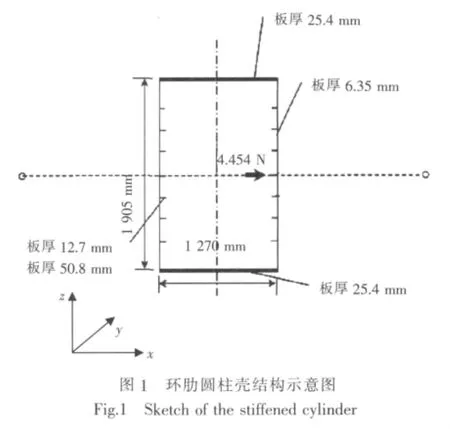
本文将以文献［11］中的环肋圆柱壳为研究对象，探讨舱壁上的圆形孔对整个结构振动性能的影响规律。环肋圆柱壳的相关参数如表1所示。用于讨论的环肋圆柱壳结构激振工况示意图如图1所示，其中激振力幅值为4.454 N，作用于极角为0°的位置，方向为径向。带孔环肋圆柱壳是在完整的环肋圆柱壳舱壁上布置一定大小、位置、数量的圆形孔，环肋圆柱壳的其他参数不变。为研究舱壁上的圆形孔对环肋圆柱壳振动性能的影响，将圆形孔的大小、位置、数量以及含圆形孔的舱壁数量设置为：圆形孔的半径为r0；以舱壁圆心为原点，x轴方向设为0°；圆形孔圆心与舱壁圆心的距离为r；圆形孔数量为k；含圆形孔的舱壁数量为m。

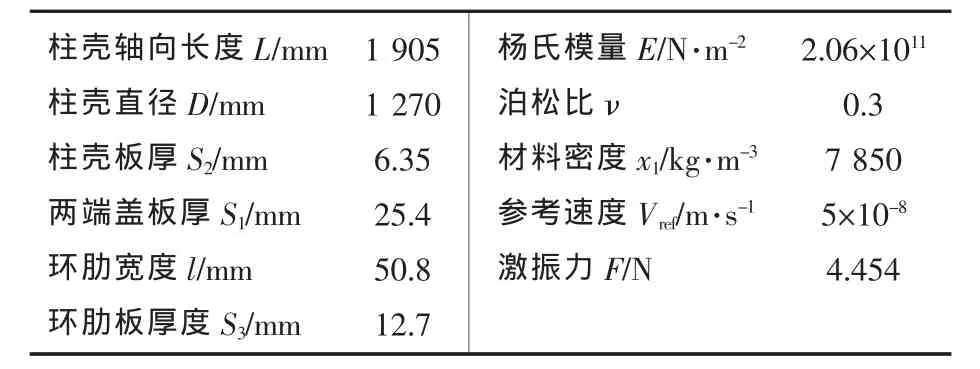
表1 环肋圆柱壳相关参数Tab.1 Parameters of the stiffened cylinder

4 有限元网格划分

本文对不同工况下的模型用PATRAN进行有限元建模，所有模型的表面与两侧端盖均使用三角形单元进行划分，肋骨使用四边形单元进行划分，在每个肋骨间距上设7个节点，6个单元。舱壁带孔模型与完整模型网格划分的主要区别是，舱壁上圆形孔附近网格划分比较密集。图2所示为部分工况下模型有限元网格划分示意图。

5 舱壁圆形孔对整个结构的表面均方法向速度级的影响

本文将采用结构有限元法，研究在单点激振力作用下，忽略结构阻尼与材料阻尼以及自由边界条件时，舱壁上圆形孔的大小、位置、数量以及含圆形孔的舱壁数量对整个结构表面的均方法向速度级的影响。激振频率取150～1 000 Hz，其中150～500 Hz的间隔频率为 5 Hz，500～1 000 Hz的间隔频率为10 Hz。不同工况的算例描述如表2所示。

5.1 圆形孔大小对整个结构的表面均方法向速度级的影响

取含圆形孔的舱壁数量m＝1，圆形孔数量k＝1，圆形孔位于舱壁中心r＝0 mm处，以圆形孔的大小为变化参数，计算结构表面振动的均方法向速度级。圆形孔大小用其半径r0进行度量，取r0=50～250 mm，间隔为50 mm。表3所示为结构真空中部分阶的固有频率（Hz）。

表2 不同工况下模型的算例描述Tab.2 Calculation models under different conditions

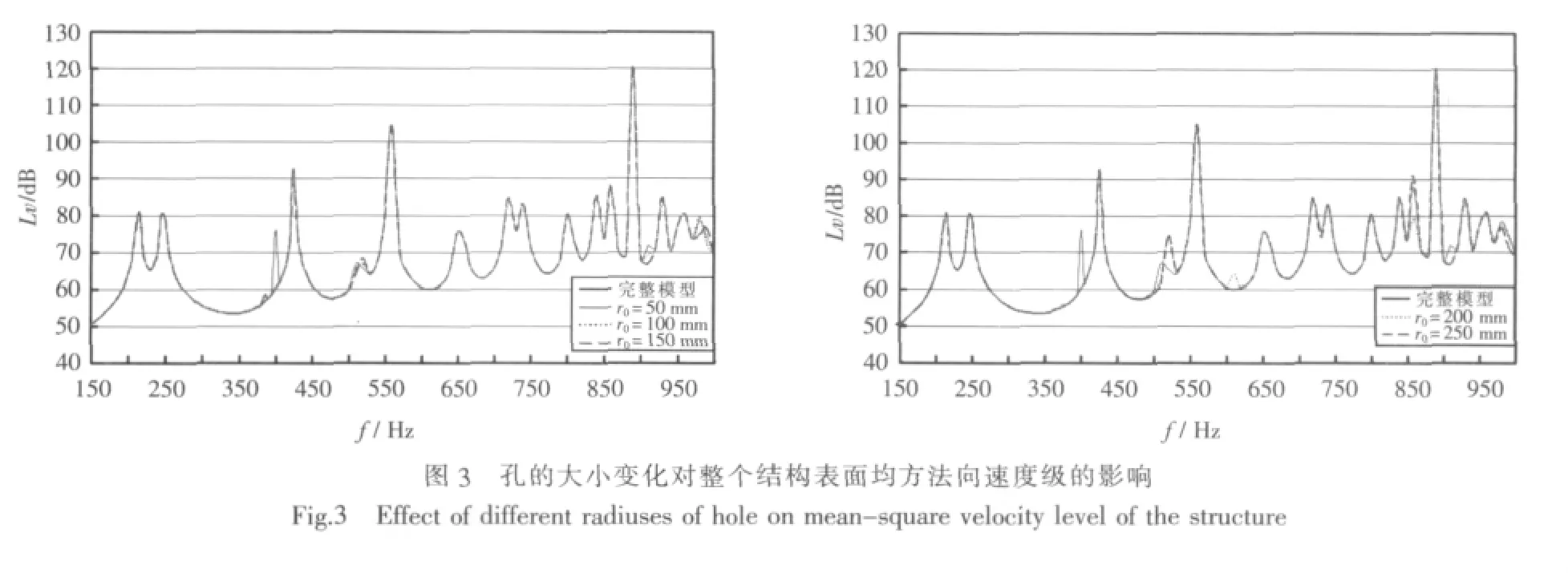
图3所示为圆形孔的大小变化时整个结构表面的均方法向速度级随激振频率变化的曲线。从图中可看出，在150～350 Hz范围内，圆形孔大小对整个结构表面的均方法向速度级影响不大；在350～1 000 Hz范围内，圆形孔大小对整个结构表面的均方法向速度级影响变大；至400 Hz时，圆形孔的大小改变了曲线幅值特性，圆形孔半径变大，幅值变小。

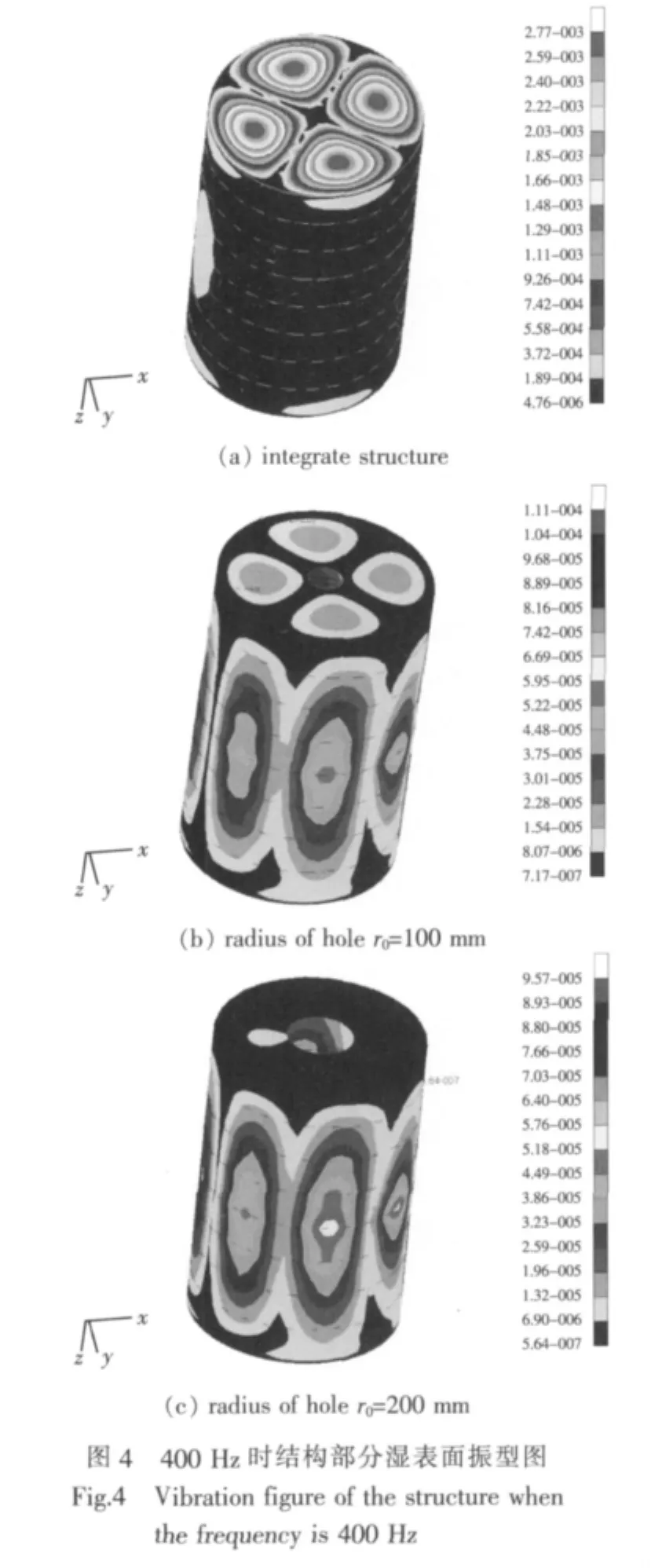
图4所示为孔的大小变化时模型在400 Hz时的振型图。从图中可看出，与完整模型相比，在此频率点下，振型有一定的差别，圆形孔半径越大，其振动幅度便越小。

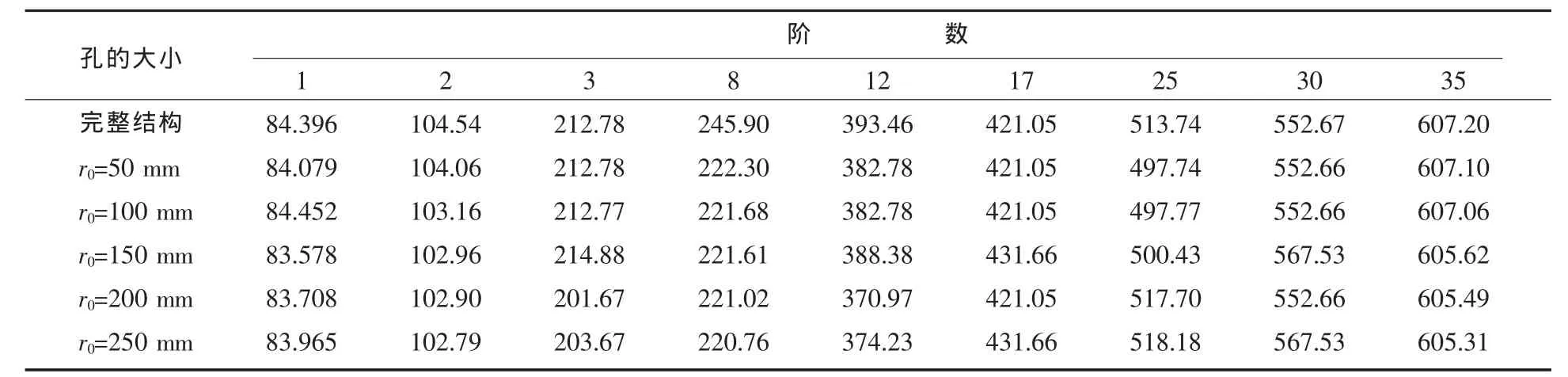
表3 结构的固有频率（工况1）Tab.3 Natural frequencies under condition 1

5.2 圆形孔位置对整个结构的表面均方法向速度级的影响

取含圆形孔的舱壁数量m＝1，圆形孔数量k＝1，圆形孔半径r0＝50 mm，以圆形孔位置为变化参数，计算结构表面振动的均方法向速度级。圆形孔的位置用孔的圆心与舱壁圆心的距离r度量，取r=0～400 mm，间隔为100 mm。表4所示为结构真空中部分阶的固有频率（Hz）。

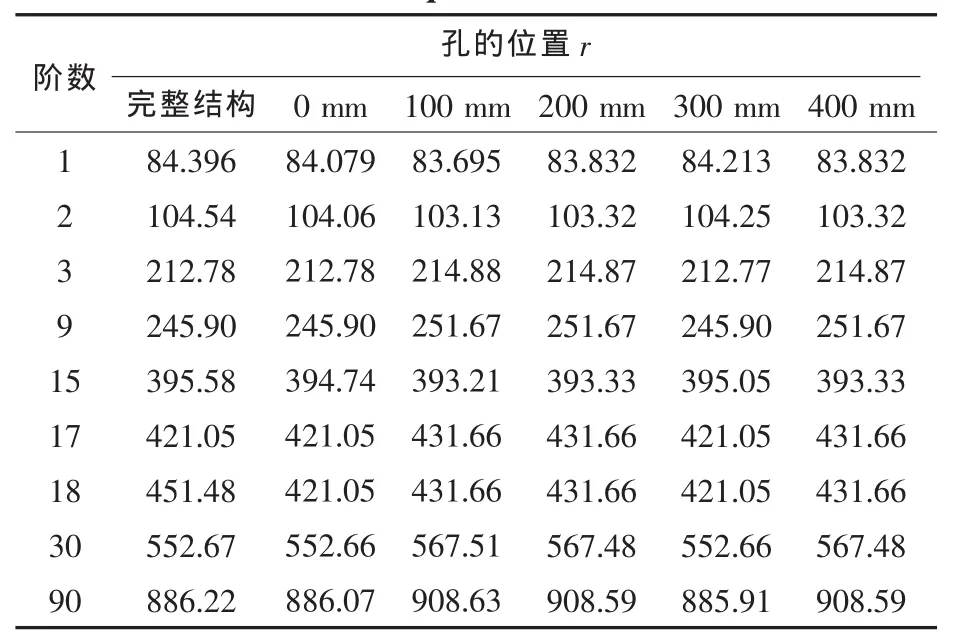
表4 结构的固有频率（工况2）Tab.4 Natural frequencies under condition 2

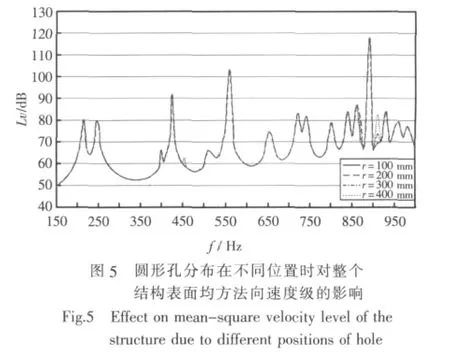
图5所示为圆形孔分布在不同位置时整个结构表面均方法向速度级随激振频率变化的曲线。从图中可看出，在150～350 Hz范围内，圆形孔的位置对整个结构表面均方法向速度级影响不大；在350～1 000 Hz范围内，在个别频率点处，圆形孔的位置改变了曲线的幅值特性。

5.3 圆形孔数量对整个结构的表面均方法向速度级的影响

取含圆形孔的舱壁数量m＝1，半径为r0＝50 mm的圆形孔均匀布置在以舱壁中心为圆心、半径r＝317.5 mm的圆周上，以圆形孔的数量k为变化参数，k 取 2，3，4，6，8。 表 5 所示为结构真空中部分阶的固有频率（Hz）。

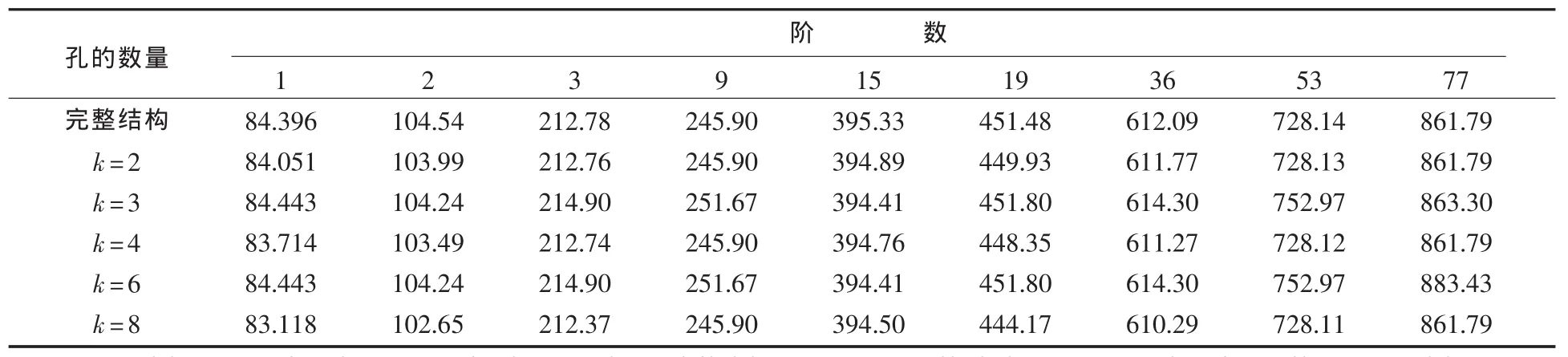
表5 结构的固有频率（工况3）Tab.5 Natural frequencies under condition 3

图6所示为圆形孔的数量不同时整个结构表面均方法向速度级随激振频率变化的曲线。从图中可看出，在150～350 Hz，圆形孔数量的变化对模型均方速度级影响不大，但随着激振频率的增大，圆形孔数量的变化对模型均方速度级影响变大；在 400 Hz、730 Hz和 980 Hz处，随着圆形孔数量的增多，改变了曲线的幅值特性。

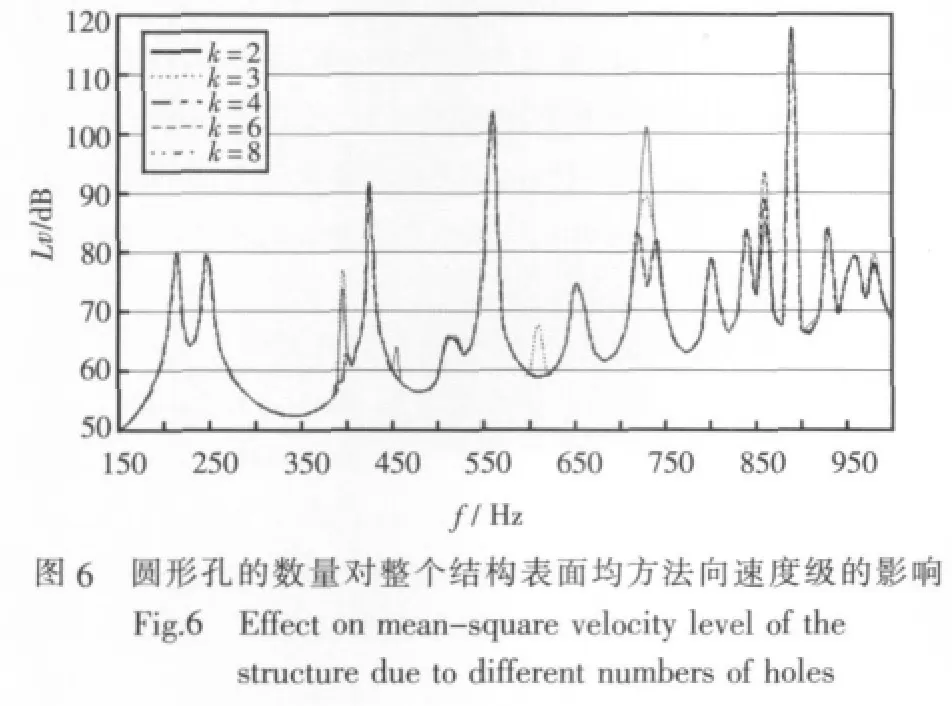
图7所示为圆形孔数量不同时模型在400 Hz时的振型图。从图中可看出，随着孔的数量增大，振型有较大差别。

5.4 含圆形孔的舱壁数量对整个结构的表面均方法向速度级的影响

取圆形孔数量k＝8，圆形孔半径r0＝50 mm，圆形孔圆心距舱壁中心r＝317.5 mm，以含圆形孔的舱壁数量为变化参数，舱壁数量m取1，2。表6所示为结构真空中部分阶的固有频率。

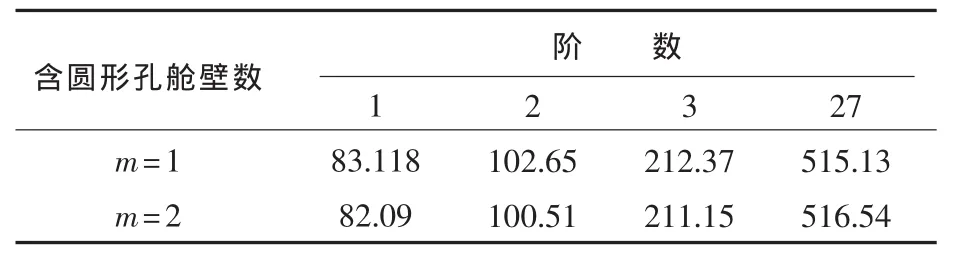
表6 结构的固有频率（工况4）Tab.6 Natural frequencies under condition 4

图8所示为含圆形孔的舱壁数量变化时整个结构表面均方法向速度级随激振频率变化的曲线。从图中可看出，在150～350 Hz范围内，含圆形孔的舱壁数量对整个结构表面均方法向速度级影响不大；在350～1 000 Hz范围内，含圆形孔的舱壁数量对整个结构表面均方法向速度级影响变大；在520 Hz处，随着含圆形孔的舱壁数量的增加，曲线峰值频率后移；至860 Hz处，随着含圆形孔的舱壁数量的增加，曲线幅值变大。

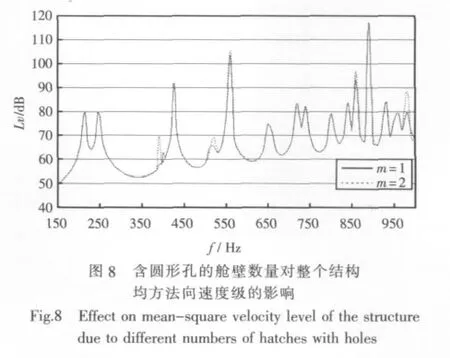
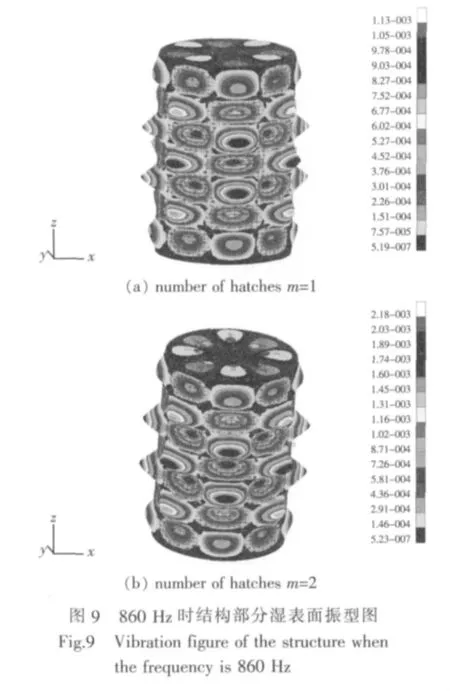
图9所示为含圆形孔的舱壁数量变化时模型在860 Hz处的振型图。从图中可看出，振型差别不大，振幅有一定的差别。

6 结 语

本文以环肋圆柱壳为研究对象，采用有限元法，计算了结构在不考虑开孔加强结构的条件下，改变圆形孔的大小、位置、数量以及含圆形孔的舱壁数量时的均方法向速度级，并对数值计算结果进行了分析。结果表明，激振频率在150～350 Hz时，4种工况对模型的均方法向速度影响不大；350～1 000 Hz时，在部分激振频率下，4种工况对模型的均方法向速度影响变大。舱壁开孔在满足工程需求的同时，可以有效减少艇体质量，但也会在一定程度上改变结构的声学特性，这是在潜艇实际设计中必须要考虑的问题。

［1］BURROUGHS C B.Acoustic radiation from fluid-loaded infinite circular cylinders with doubly periodic supports［J］.Journal of the Acoustical Society of America，1984，75（3）：715-722.

［2］YOSHIKAWA S，WILLIAMS E G，WASHBURN B.Vibration of two concentric submerged cylindrical shells coupled by the entrained fluid［J］.Journal of the Acoustical Society of America，1994，95（6）：3273-3286.

［3］LAULAGNET B，GUYADER J L.Sound radiation by finite cylindrical ring stiffened shells［J］.Journal of Sound and Vibration，1990，138（2）：173-191.

［4］曾革委，黄玉盈，马运义.舱壁和环肋加强的无限长圆柱壳声弹耦合模型及其声特性［J］.固体力学学报，2002，23（3）：269-279.ZENG G W，HUANG Y Y，MA Y Y.Acoustic radiation from fluid-loaded infinite cylindrical shell stiffened by rings and bulkheads［J］.Acta Mechanica Sodida Sinica，2002，23（3）：269-279.

［5］陈美霞，骆东平，王祖华，等.激励力对双层圆柱壳声辐射性能的影响［J］.船舶力学，2005，9（2）：124-130.CHEN M X，LUO D P，WANG Z H，et al.Effect of driving forces property on characteristics of sound radiation from finite double cylindrical shell［J］.Journal of Ship Mechanics，2005，9（2）：124-130.

［6］谢志勇，周其斗，纪纲.双层柱壳的流固耦合模态计算与试验研究［J］.海军工程大学学报，2009，21（2）：97-101.XIE Z Y，ZHOU Q D，JI G.Computation and measurement of double shell vibration mode with fluid load［J］.Journal of Naval University of Engineering，2009，21（2）：97-101.

［7］艾海峰，陈志坚，孙谦.降低双层加肋圆柱壳低频噪声的声学设计技术［J］.噪声与振动控制，2007，27（3）：106-109.AI H F，CHEN Z J，SUN Q.Acoustics design to depress the low frequency noise of the ring-stiffened cylinder with double-shell［J］.Noise and Vibration Control，2007，27（3）：106-109.

［8］王路才，周其斗，纪刚，等.以舱段模型代替整艇模型进行噪声估算的可行性探讨［J］.中国舰船研究，2010，5（6）：26-32.WANG L C，ZHOU Q D，JI G，et al.Approximate method for acoustic radiated noise calculation of sub cabin model in replacing full-scale model［J］.Chinese Journal of Ship Research，2010，5（6）：26-32.

［9］白雪飞，郭日修.带有损伤凹陷的环肋圆柱壳应力和稳定性分析［J］.海军工程大学学报，2010，22（3）：76-83.BAI X F，GUO R X.Analysis of stress and stability of damaged ring-stiffened cylindrical shell［J］.Journal of Naval University of Engineering，2010，22（3）：76-83.

［10］刘监波，刘文玺，周其斗，等.水下结构物舱壁振动控制的结构参数优化研究［J］.中国舰船研究，2010，5（6）：21-25.LIU J B，LIU W X，ZHOU Q D，et al.Optimal parametric design of bulkhead vibration control for under water structure［J］.Chinese Journal of Ship Research，2010，5（6）：21-25.

［11］CHEN L H，SCHWEIKERT D G.Sound radiation from an arbitrary body［J］.Journal of the Acoustical Society of America，1963，35（10）：1626-1632.