Bayes条件下非线性模型参数估计的渐近展开
吴一凡
(江苏食品职业技术学院 基础教学部, 江苏 淮安 223003)
Bayes条件下非线性模型参数估计的渐近展开
吴一凡
(江苏食品职业技术学院 基础教学部, 江苏 淮安 223003)
给出了在Bayes条件下非线性回归模型的参数估计,建立了非线性回归模型的几何结构,推广了Bates和Wates关于非线性回归模型的几何框架,用几何方法求出参数估计的随机展开,并讨论了若干与统计曲率相关的渐近性质,给出了该模型的极大似然估计的方差和偏差的近似表示.
Bayes条件;非线性模型;几何结构;渐近展开
0 引言
Bates和Watts[1]在Euclid空间引入了非线性回归模型的曲率度量,Zhong[2]对非线性随机效应模型在Euclid空间建立了几何结构,并研究了该模型参数和子集参数的三种置信域.本文在Bayes条件下对非线性回归模型建立了类似Bates和Watts的几何结构,并用几何方法求出参数估计的随机展开,并讨论了若干与统计曲率相关的性质.
1 Bayes条件下非线性回归模型
Bayes条件下非线性回归模型可表示为
Y=f(X,β)+ε,ε~N(0,σ2In),β~N(0,σ2∑)
(1)
其中Y=(y1,y2,…,yn)T是n×1观测向量,∑为p×p阶正定阵,β=(β0,β1,…,βp-1)T为p×1未知参数向量,ε为n×1随机误差向量.模型(1)的对数似然函数可以表示为

(2)
(2)式对β求导,得到模型的Score函数为
(3)
其中Dβ=∂f(X,β)/∂β.模型(1)的观察信息阵为
(4)
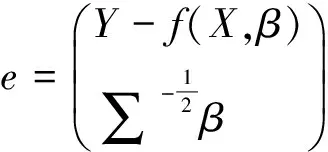
2 非线性回归模型的几何结构
在Rn+p欧氏空间中,定义p维曲面π:η=η(β),设
Ca:Ca(t)=η(β1,…,βa-1,βa+t,βa+1,…,βp),a=1,…,p.
其中t是实数,Ca称为π在β处的坐标曲线.设D的QR分解为
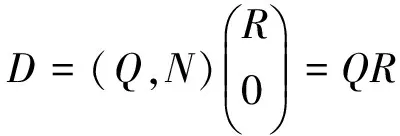
(5)
其中R为p阶具有正对角元的上三角矩阵,Q,N分别为(n+p)×p和(n+p)×n阶列正交矩阵,其列向量构成π在β处的切空间和法空间的标准正交基,即Q,N满足
QTQ=Ip,QTN=0,NTN=In
(6)
其中Ip和In分别表示p阶和n阶单位矩阵.
模型(1)的固有曲率立体阵AI和参数效应曲率立体阵AP分别定义为
AI=[NT][U],AP=[QT][U]
(7)

3 估计量的随机展开

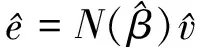
(8)
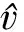
由Wei[3]以及He and Huang[4]的结果不难知道该模型有
(9)
该式下文将反复用到,为了给出随机展开,先给出几个引理.
引理1 对模型(1),且满足Wei[3]关于模型的正则条件及以上假设成立,则
(10)

DTF=-RTAIR
(11)
证明参见Wei[3]
定理1 若模型(1),在引理1条件成立的条件下,则Δβ的随机展开可表示为
(12)
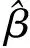
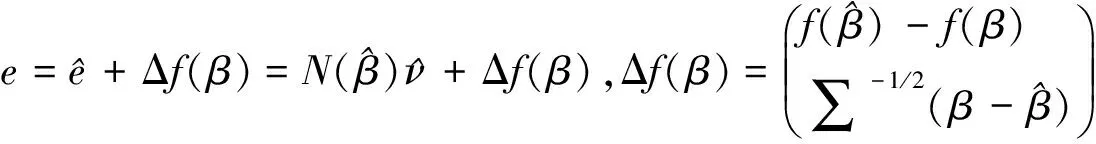
则由引理1得
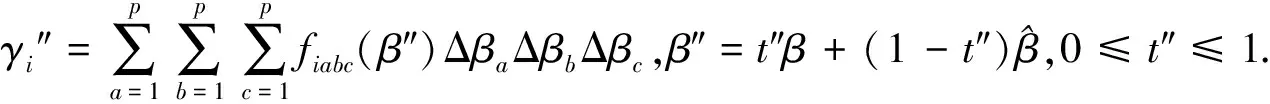
将上式两边分别同乘以DT与NT得:


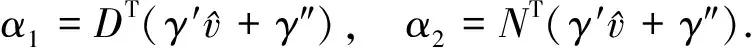
(13)

(14)

等式(12)式表明Δβ的随机展开式取决于模型的固有曲率和参数效应曲率,这些结果同Wei[5],[3]一致.
由Δβ的随机展开式,可得到计算偏差和方差的近似公式.也可得到偏差和方差的近似公式.主要计算τ和λ的各阶矩阵.为此,给出以下引理.
E(τTAτ)=σ2tr[A],cov(τTAτ,τTBτ)=(αij)
(15)
其中αij=2σ4tr(AiBj),Ai和Bj分别是立体阵A和B的第i面和第j面,tr[A]表示立体阵的迹(见Wei[3]附录A),证明参见Wei[3].
(16)
证明由于E(τ)=0,因此由定理1可知

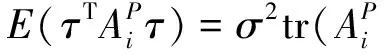
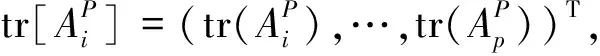
因此(16)式成立.
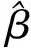
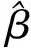
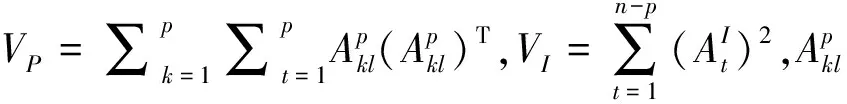
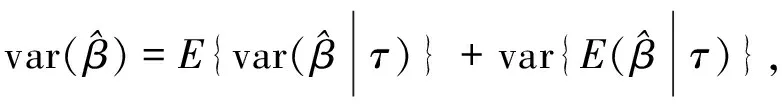
则由定理1可得:
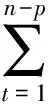
另一方面,利用定理1及引理2得
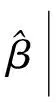
综合上述结果,定理3的结论成立.
这个定理的内容和形式与文献(Amari[6],Efron[7],Wei[8],Wei[3])的结果都是一致的.定理3结论的第一项为CR下界,第二项仅与固有曲率有关,第三项则与参数效应曲率有关.
[1] Bates D M, Watts, D G. Relative curvature measures of nonlinearity[J]. J Roy Statist Soc Ser B, 1980,42,1-25.
[2] Zhong X P, Meng G M, Wei B C. On Confidence Region of Nonlinear Models with Random Effects[J]. Mathematica applicata, 2000,13(4):100-105.
[3] Wei B C. Exponential Family Nonlinear Models[M]. Singapore:Springer-Verlag,1998.
[4] He S, Huang X. Central limit theorem of linear regression model under right censorship[J]. Science (seriesA),2003,46(5):600-610.
[5] 韦博成.近代非线性回归分析[M]. 南京: 东南大学出版社,1989.
[6] Amari S. Differential Geometry Method in Statistics[M]. Berlin: Lecture Notes in Statistics,1985,28.
[7] Efron B. The geometry of exponential families[J]. Ann Staist,1975,3:1189-1242.
[8] 韦博成,鲁国斌. 统计诊断引论[M]. 南京: 东南大学出版社,1991.
[责任编辑:李春红]
AsymptoticExtensionofNonlinearModelswithBayesianConditions
WU Yi-fan
(Jiangsu Food Science College, Huaian Jiangsu 223003, China)
In this paper, we propose a differential geometric framework for nonlinear model under Bayesian conditions. Our framework may be regarded as an extension of that presented by Bates & watts for nonlinear regression models. We use this geometric framework to discuss the parameter stochastic expansion by using the curvature in the nonlinear model. Some statistical properties of parameter are studied from the geometric point of view.
bayesian condition; nonlinear model; geometric framework; asymptotic extension
O212.1
A
1671-6876(2012)03-0226-04
2012-04-23
吴一凡(1980-), 男, 江苏沭阳人, 讲师, 硕士, 研究方向为应用概率统计.

