近水面作业的机器人综合减摇研究
张立华,吴宏圣,张 杰
(1.中国科学院长春光学精密机械与物理研究所 光电技术研发中心,长春 130033;2.一汽轿车股份有限公司 产品部电气系统科,长春 130033)
近水面作业的机器人综合减摇研究
张立华1,吴宏圣1,张 杰2
(1.中国科学院长春光学精密机械与物理研究所 光电技术研发中心,长春 130033;2.一汽轿车股份有限公司 产品部电气系统科,长春 130033)
近水面作业的机器人会受到波浪干扰力的影响,很难保持稳定的姿态。根据机器人近水面作业时所受到的波浪干扰力的计算方法和机器人六自由度模型的状态空间表达式,计算出适用于变结构控制器的状态空间方程。在此基础上进行了积分变结构控制器的设计过程,然后借助Matlab软件,对机器人的横摇、纵摇运动中带有PID控制器和带有变结构控制器两种情况分别进行仿真,经过对比分析,变结构控制器较好的控制了机器人的姿态。
近水面机器人;运动模型;综合减摇;积分变结构控制器
开发海洋资源是人类一直面临的重大课题,因此开发海洋作业的机器人成为各国的重点研究之一。我国在本世纪初也开展了水下机器人的设计研究,取得了很多成就,如沈阳自动化研究所设计的水下机器人可以在环境恶劣的条件下救助落水者[1],哈尔滨工程大学在减摇控制方面也进行了很多理论研究[2,3,4,5]。在近水面机器人的控制算法中,变结构控制(即滑模控制)因其滑动面的设计与控制对象的参数以及各种干扰无关,而且响应快、对参数和外干扰变化不灵敏、物理实现简单等优点,成为在机器人近水面控制的主要应用[6]。
传统的机器人的姿态控制中,控制翼一般被用来控制航向、纵倾角、横倾角、深度等,而不控制横摇和纵摇。控制翼在进行运动控制时,左右两弦的翼转动方向和角度是一样的。本文对机器人在近水面作业时产生的横摇与纵摇运动进行研究,在首鳍处于自然状态,保持机器人定深情况下,尾鳍可以像减摇鳍一样作方向相反的转动,以产生减摇力矩。设计的控制系统可以控制尾鳍的动作进而对横摇及纵摇进行减摇[7]。
1 海浪干扰的描述
在本文的研究中,我们应用了图1所示的机器人作为研究对象,其六自由度运动的动力学模型在文献[8]中有很好的介绍及研究。

图1 水下机器人模型
水下机器人在近水面作业时,会受到波浪干扰力的作用[5],姿态很难保持稳定。计算水下机器人在近水面处运动时所受到的波浪干扰力,可以参考近水面处运动的潜艇受到的干扰力的计算方法。
经过计算得到一阶波浪力的计算公式如式(1):

二阶波浪力(波吸力)的计算公式如式(2):

海浪施加在近水面水下作业的机器人的干扰力,可以看作是一阶波浪力与二阶波浪力的合力[6],因此得到波浪干扰力的表达式,如式(3):

2 近水面机器人六自由度模型分析
近水面机器人可以视为刚体,因此机器人六自由度空间模型如下[7]:

3 积分变结构控制器的设计
设计合理的切换函数以及正确的变结构控制规律是变结构控制器的关键问题。根据多输入非线性系统化为可控正则型的方法[10],将近水面作业的水下机器人的六个自由度模型化为可控正则型。


变结构控制系统的切换面:
S=[s1s2s3s4s5s6]T=CX=[C1e1C2e2C3e3C4e4C5e5C6e6]T,切换面是独立于控制的,可以通过极点配置法来确定C。
对于第i个子系统,可以用下式为其简约型的表达式:

为了削弱抖振,本文选择等速趋近率,如下式

将式(19)带入式(20),得到水下机器人基于指数趋近率的变结构控制器,如下式:

4 系统仿真分析
近水面作业的机器人由于受到波浪干扰力和力矩的影响,运动状态将会发生非常大的变化,同时姿态也会很快的变化,姿态将很难维持稳定[11]。此时,必须快速和实时控制近水面作业的机器人的姿态,因此需要横摇系统和纵摇系统做出很快的响应。所以六个子系统的极点值如下[12]:子系统一和子系统三的极点值是Λ1=Λ3={-0.06},子系统二和子系统四的极点值是Λ2=Λ4={-0.05},子系统五和子系统六的极点值是Λ5=Λ6={-0.03}。由前面切换面的计算公式可以得到切换面为:C1=C3=[0.06,1],C2=C4=[0.05,1],C5=C6=[0.03,1]。
假定在海浪的有义波高为0.88m,距离水面3m处,近水面机器人的航行速度为6m/s,海浪遭遇角为90°,此时,近水面机器人由于受到海浪力的干扰,姿态很难保持稳定[13]。经过Matlab仿真,图2和图4分别是带有普通PID控制器的近水面机器人的横摇角和纵摇角随时间的变化图形。
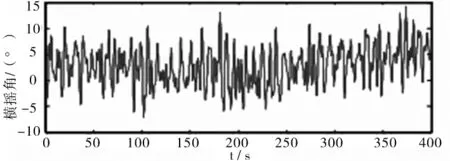
图2 PID控制器减摇时的横摇角

图3 变结构控制器减摇时的横摇角
机器人的首鳍用于控制水下潜水的深度,尾鳍用于控制水下机器人保持姿态[8]。图2可以看出整个运动过程中,横摇角度值在0角度处左右变化,并且变化幅值很大,最大值达到15°,可以看出角度变化曲线的对称轴在0角度轴以上。因此可以推测,因为受波浪力的作用,且波浪遭遇角为90°,虽然有PID控制器保持姿态,但近水面机器人横摇角一边的摇摆幅值大于另一边的摇摆幅值,很可能会发生侧翻。而图3变结构控制器控制的近水面机器人,可以看出横摇角度值在0角度值处变化,并且变化幅值很小。
图4可以看出整个运动过程中,纵摇角度值在0角度处上下变化,并且变化幅值很大,最大值达到12°。尤其在60s至120s的仿真阶段,纵摇角度值始终在0角度值上。而图5变结构控制器控制的近水面机器人,可以看出纵摇角度值在0角度处变化,并且变化幅值非常小。因此,本文设计的控制器能够较好的控制近水面作业机器人姿态运动。

图4 PID控制器减摇时的纵摇角

图5 变结构控制器减摇时的纵摇角
根据常用评估减摇装置效果的方法,借助式(22)来评价减摇效果[14]。

根据上述公式计算了近水面机器人的减摇效果,计算结果见表1:
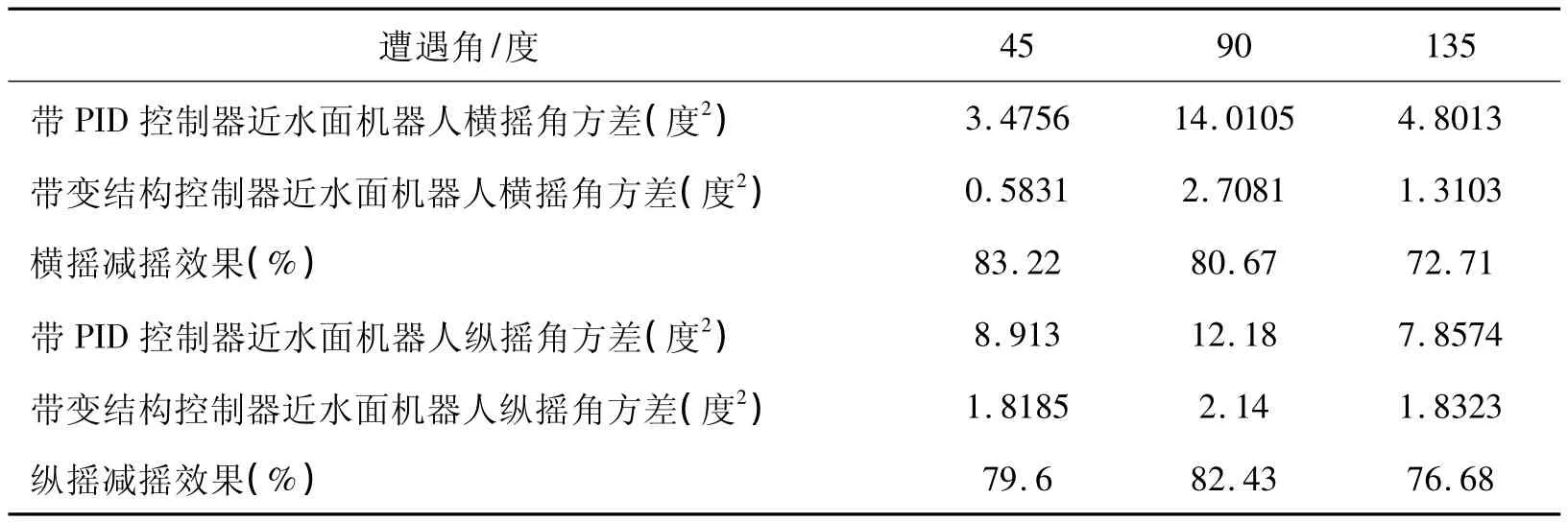
表1 减摇效果对比表
5 结语
本文首先分析了近水面作业的机器人受到的海浪干扰力和干扰力矩的计算方法,根据机器人实际航行状态分析得到近水面航行状态下机器人六自由度运动模型,针对近水面作业的机器人运动模型存在的非线性和耦合性设计了基于积分变结构控制策略的控制器。借助Matlab仿真软件对系统进行仿真,仿真结果表明,在本文设计的控制器控制下机器人综合减摇取得了较好的减摇效果,并且具有系统抖振小,动态性能良好等优点。
[1] 李波.水下无人航行器发展研究[D].西安:西北工业大学,2001.
[2] 金鸿章,綦志刚,罗延明,等.基于Weis-Fogh机构的零航速减摇鳍升力模型的研究[J].系统仿真学报,2007,19(17):4079-4081.
[3] 金鸿章,罗延明,綦志刚,等.基于Weis-Fogh机构的零航速减摇鳍升力特性研究[J].哈尔滨工程大学学报,2007,28(7):762-767.
[4] 金鸿章,张晓飞,罗延明,等.零航速减摇鳍升力模型研究[J].海洋工程,2007,25(3):83-87.
[5] 金鸿章,姚绪梁.船舶控制原理[M].哈尔滨:哈尔滨工程大学出版社,2001.
[6] 张瑾,连琏,葛彤.潜艇近水面运动鲁棒控制及仿真研究[J].海洋工程,2006,24(4):32-37.
[7] 金鸿章,李国斌.船舶特种装置控制系统[M].北京:国防工业出版社,1995.
[8] Peter Michael Ostafichuk.AUV hydrodynamic and modeling for improved control[D].Canada:University of British Columbia,2004.
[9] 李晔,刘建成,徐玉如,等.带翼水下机器人运动控制的动力学建模[J].机器人,2005,27(2):128-131.
[10] 朱计华,苏玉民,李晔,等.AUV近水面运动的积分变结构控制及仿真[J].系统仿真学报,2007,19(22):5321-5324.
[11] Lionel Lapierre,Bruno Jouvencel.Robust Nonlinear Path-Following Control of an AUV[J].OCEANIC ENGINEERING,2008,33(2):89 -102.
[12] 张杰.近水面作业的机器人综合减摇机理研究[D].哈尔滨:哈尔滨工程大学,2010.
[13] Ming-Chung,Fang Pei-En Chang,Jhih-Hong Luo.Wave effects on ascending and descending motions of the autonomous underwater vehicle[J].OCEAN ENGINEERING,2006,33(2006):1972 -1999.
[14] 金鸿章,王龙金,李冬松,等.零航速减摇鳍升力模型分析及系统仿真研究[J].武汉理工大学学报(交通科学与工程版),2008,32(5):775-77.
Research on Integrated Stabilization for Robot Working Near Sea Surface
ZHANG Li-hua1,WU Hong-sheng1,ZHANG Jie2
(1.Center for Photoelectric Technology Development,Changchun Institute of Optics,Fine Mechanics and Physics of Chinese Academy of Sciences,Changchun 130033,China;2.Section of Electrical System of Product Division,FAW Car Co.,Ltd,Changchun 130033,China)
The robots working near sea surface will be influenced by wave force and they are difficult to maintain a stable state.According to the calculation method of wave force that influences robots working near the sea surface and the state space representation of the robot six-degree-freedom model,the state space equation which is suited to integral variable structure controller is calculated.Then the process of integral variable structure controller for robot is designed.By Matlab software,we simulate the roll and pitch motion with PID controller and with the integral variable structure controller.Through comparison,integral variable structure controller can better control robot’s state.
near-sea-surface robot;motion model;integrated stabilization;integral variable structure controller
U666
A
1009-3907(2012)08-0918-05
2012-06-05
张立华(1984-),女,吉林长春人,研究实习员,硕士,主要从事自动控制、嵌入式系统方面研究;吴宏圣(1974-),男,吉林长春人,副研究员,硕士,主要从事光电位移检测技术方面研究。
责任编辑:吴旭云

