前缘后掠式栅格翼升阻特性研究

邓 帆，陈少松

（南京理工大学能源与动力工程学院，江苏 南京 210094）

0 引 言

栅格翼作为一种非常规翼面，受阻力大这个缺点的限制使得栅格翼很少作为弹箭的升力翼面使用，对栅格翼减阻增升的研究一直是栅格翼应用的主要方向，Mark S Miller在94年的论文中进行了Ma＝0.5～2.5栅格翼外形参数对阻力特性影响的风洞实验［1］；其后陈少松进行了超声速Ma＝2.521下栅格翼减阻特性的风洞实验［2］；P Theerthamalai通过数值方法研究了栅格翼单个栅格的几何参数在超声速阶段对栅格翼气动性能的影响［3］。这些研究者包括雷娟棉及吴小胜等人在栅格翼减阻问题上主要是考虑改变栅格翼的筋厚度、边框的剖面形状以及栅格的翼弦格宽比等参数的改进和匹配来进行减阻［4－5］。近期Cai J S及Zeng Y采用数值方法对其提出的翼面后掠方式进行了研究［6－7］，这种设计方式对减阻有一定的影响，可通过翼面后掠改善超声速阶段栅格内部的气流壅塞现象达到减阻目的。

超声速下栅格翼的阻力主要是来自波阻，减少波阻的有效途径是减弱激波的强度，由于栅格翼的迎风面是一个平面，当激波不能被栅格吸入的时候，在栅格翼的前缘将形成弓形正激波，这将极大的增加激波产生的阻力，如能采取措施将激波吸入栅格，将会极大的减少激波的强度，减少阻力。前缘后掠可以使弓形激波消失，在栅格上形成斜激波，因此是目前寻求栅格翼减阻的一种有效的设计方法，由此本文提出一种前缘后掠式的栅格翼设计，通过数值方法对不同翼面后掠方式及后掠角度对栅格翼的减阻特性进行了详细研究。

1 数值方法

1.1 控制方程

曲线坐标系下的雷诺平均N－S方程：

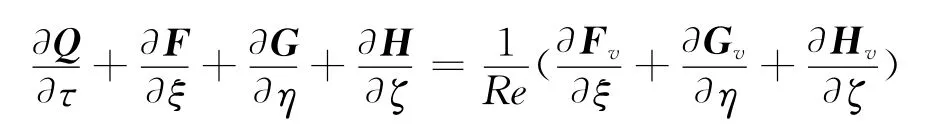
式中，Q表示守恒变量矢量，F、G和H 表示无粘通矢量，Fv、Gv和Hv表示粘性通矢量。采用有限体积法对空间进行离散，离散格式采用AUSM＋，时间项采用隐式LU－SGS方法。湍流模型采用Realizable k－ε模型，并使用带双层模型的增强壁面函数。

1.2 边界条件

远场边界条件：采用自由流条件，入流边界采用来流值。

物面边界条件：采用无滑移条件。

1.3 网格生成及计算条件

栅格内部的激波边界层对栅格流场特征有重要影响，因此粘性边界层和激波分辨率模拟的好坏对计算结果准确性有关键作用。模型网格均采用能有效模拟粘性流动的六面体结构网格，以模型GS的弦长b作为参考长度，网格周向远场LRB＝8b，轴向远场LAB＝10b，网格第一层距离物面距离为HBL＝1.5×10－5b，以确保y＋＜1，网格数量在80万～150万之间。

计算条件为：Ma＝1.5～4.5，α＝0°、8°，T＝288K，P＝101325Pa，采用集群并行运算系统进行计算，并行环境为30个处理节点的集群服务器，其中每个计算节点为4核AMD Opteron8374 2.2G处理器和大小为16G的内存。

2 研究模型

设计了3组研究模型，第一组3个模型，包括1个翼面无后掠的模型和2个前缘后掠的模型，具体参数见图1，模型的框架尺寸相同，如图1（a），前缘后掠的模型根据后掠中心位置的不同分为模型GP 55SA和模型GV 55SA，模型GP 55SA为栅格格间交接点为尖点的后掠方式，模型GV 55SA为栅格边框中心为尖点的后掠方式，升力面上的前缘后掠角为55°，侧壁上的前缘后掠角62°，2个模型的升力面积与无后掠模型GS的升力面积相等。

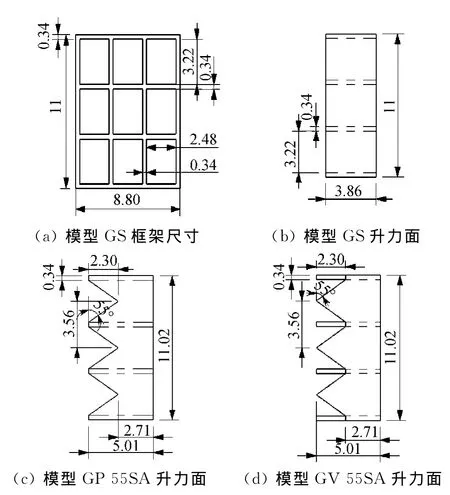
图1 不同前缘后掠方式栅格翼模型工程图Fig.1 Engineering map of windward swept grid fins

第二组模型为前缘不同后掠角度的5个研究模型，对采用栅格格间交接点后掠的模型进行研究，在保证升力面积相同的前提下，研究不同后掠角度对栅格翼减阻效果的影响。模型基本框架尺寸采用模型GP 55SA的尺寸，通过改变弦长来保证升力面积的相同，栅格翼升力面上的前缘后掠角度变化范围φ1＝25°～65°，等差10°，相对应的栅格翼侧壁上的前缘后掠角度变化范围φ2＝31°～70°，以保证升力面的齿根和侧壁栅格的齿根处在同一平面上，5个模型的最大弦长范围b＝4.24～5.29mm，模型的升力面尺寸如图2。

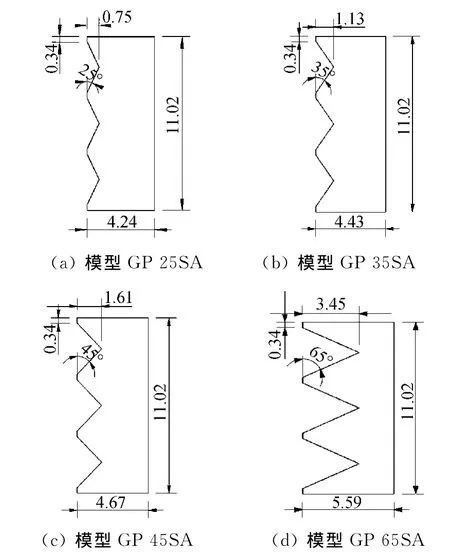
图2 不同前缘后掠角度栅格翼模型升力面工程图Fig.2 Engineering map of swept angle grid fins'lift surface

第三组为贴体型栅格翼模型，由于今后对武器的要求是尽量内置于武器舱内，以增强飞行器的隐身性和整体减阻的需要，对于战术导弹或小直径炸弹而言，采用栅格尾翼的好处之一是可将栅格翼折叠于弹体之上，减小所需安装空间，因此对贴体型前缘后掠式栅格翼模型GP 55SAH的气动特性进行研究，比较研究模型为栅格翼背风面为平面的栅格翼模型GP 55SA，同样在升力面相同的前提下，比较两者升阻特性的不同。3组研究模型中栅格翼的基本尺寸均来源于加拿大国防研究与发展中心（Defence R＆D Canada，简称为DRDC）和法德联合研究所（French－German Research Institute of Saint－Louis，简称 为ISL）进行风洞实验研究模型A3的栅格尾翼［8］，其中模型A3弹身直径D＝20mm，因此贴体型栅格翼模型的背风面尺寸如图3（c）中所示。3组栅格翼模型的部分计算网格如图4所示，统一参考长度Lr＝3.864mm，参考面积Sr＝213mm2，俯仰力矩的参考点为原点位置，即迎风面中心处。

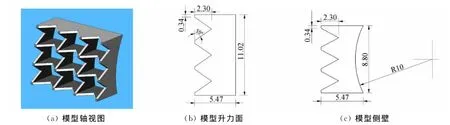
图3 贴体型前缘后掠式栅格翼模型GP 55SAH工程图Fig.3 Engineering map of curve leeward gird fin

图4 栅格翼模型计算网格Fig.4 Computational mesh of gird fins

3 计算结果及分析

因为研究的来流范围是超声速阶段，在此期间模型的阻力主要由波阻产生，因此减小栅格翼的波阻成为改善其气动特性的重要目标，第一组栅格翼模型零升波阻CWD0随马赫数变化的变化曲线如图5所示，可见模型GS的零升波阻随马赫数增加变化不大，其余2种模型的零升波阻和模型GS相比较有明显减小，并且这种减阻效果随马赫数增加而增大，其中模型GP 55SA减阻率最大为47%，模型GP 55SA与模型GV 55SA比较，差别在于前者的尖前缘位于栅格4个翼面的交接处，尖化的交接点使得交接点处的激波大大减弱，而模型GV 55SA的交接凹齿位于4面翼的交接点，4面翼上齿尖的斜激波汇聚到凹齿处产生强度较大的激波区，因此比较而言模型GP 55SA的减阻效果更好。图6为第二组栅格翼模型的波阻CWD随马赫数的变化曲线，其中攻角α＝8°，可见除后掠角φ1＝25°的模型GP 25SA以外，和标准模型GS相比较，其余4个模型的波阻都有明显减小，并且是随着后掠角的增大减阻效果依次增加，值得关注的是模型GP 25SA在Ma＝2.5时的波阻，大于前缘无后掠的模型GS，主要原因应是弦长的增加，同时后掠角度过小，使得前缘后掠对减小波阻方面的影响小于弦长增加对气动壅塞现象的贡献。第三组栅格翼模型的波阻CWD随马赫数的变化曲线如图7，贴体型前缘后掠模型GP 55SAH的波阻在Ma＜3.5之前略大于栅格翼背风面无弧度的模型GP 55SA，但在Ma＞3.5之后情况相反，可见随马赫数的增加，这种贴体型的设计效果更好。

图5 第一组模型CWD0随Ma的变化Fig.5 CWD0of Group 1vs.Ma

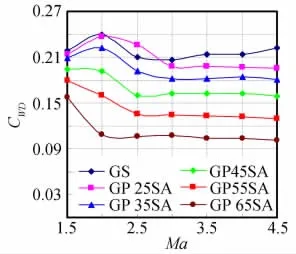
图6 第二组模型CWD随Ma的变化Fig.6 CWDof Group 2vs.Ma

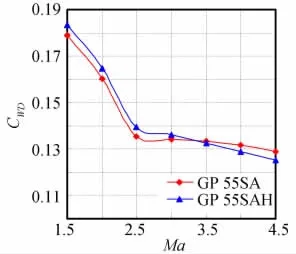
图7 第三组模型CWD随Ma的变化Fig.7 CWDof Group 3vs.Ma

为比较不同栅格翼模型栅格内部的流场发展，对于不同前缘后掠方式的栅格翼模型，在Y－Z平面上截取2个截面，对比分析马赫数的发展情况，因为激波的产生和交叉影响区集中在齿尖和齿根之间，取这两点的中截面（X1＝1.15mm）及齿根处的截面（X2＝2.32mm），图8为Ma＝3.5时2种模型中心位置处的栅格在攻角α＝8°时2个截面上的马赫数分布情况，可见和模型GV 55SA相比，模型GP 55SA栅格内部的高速区分布范围更广，在栅格壁之间的交叉处流场的减速现象并不严重，气流在向后发展的过程中，主要的减速区集中在栅格壁之间的中线部分，如图8（c）所示，而模型GV的马赫数分布情况则恰恰相反，栅格翼在栅格壁交叉处的低马赫数区域说明在这个区域气流壅塞的现象比较严重。

对于不同前缘后掠角度的栅格翼模型，在X－Y平面内截取截面Z＝0mm，穿过栅格翼升力面中线，即带前缘后掠角度模型的最短弦长处截面，标准模型GS、2个带前缘后掠角度模型GP 25SA及GP 65SA在Ma＝2.5，α＝8°时截面Z上的马赫数分布图如图9所示，可见图9中（a，b）的马赫数最大值相同，但模型GV 25SA的迎风面弧形激波强度明显大于标准模型GS，波后的蓝色低速区面积也大于模型GS，说明在升力面积相同的情况下，不是所有前缘带后掠角度的方案都能有效减阻，因为翼面的后掠，弦长相应增加后，增大了栅格内部气流通过的距离，同时增加了气流出现阻滞的可能性，图9（c）显示带后掠角φ1＝65°的模型GP 65SA流场中最大马赫数为2.76，同时前缘处凹齿前方由强度较弱的斜激波取代了图9（b）中模型GV 25SA所出现的弧形激波，栅格内部的流场无连续的低速区出现，说明气流壅塞现象得到明显改善。

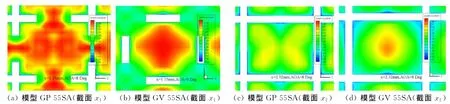
图8 不同前缘后掠方式栅格翼模型的马赫数分布图Fig.8 Mach number distribution of windward swept grid fins

图9 不同前缘后掠角度栅格翼模型的马赫数分布图（截面Z）Fig.9 Mach number distribution of swept angle grid fins（Section Z）

图10为第一组模型的升力系数CL随马赫数的变化曲线，可见前缘后掠的方式在减小气流壅塞的同时，因为栅格内流速的提高，使得在Ma＝2.5前后的很大马赫数范围内模型的升力系数得到明显提高，升力系数的最大增长率达到41%。图11为第二组模型的升力系数CL随马赫数的变化曲线，由图可见当前缘后掠角度为φ1＝25°、35°时，均会产生更强的气流壅塞现象，致使升力系数下降，在Ma＝2.5前后低于模型GS，当φ1≥45°后，升力系数逐渐回升并超过前缘无后掠的栅格翼，同时发现在φ1≤45°的范围内，随马赫数的增加，升力系数的大小趋于一致，而φ1≥55°的模型升力系数则会有所下降。图12为第三组模型的升力系数CL随马赫数的变化曲线，可见贴体型模型GP 55SAH在升力特性方面要略好于背风面为平面的前缘后掠式模型GP 55SA，通过图13可看出Ma＝2.5时两种模型在截面Z上的不同压强分布情况，模型的升力主要是由栅格上下壁面的压力差产生，不同的是和模型GP 55SA比较而言，背风面带弧度的模型GP 55SAH前缘处栅格下壁面有更明显的连续高压区。

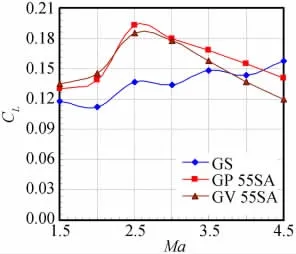
图10 第一组模型CL随Ma的变化Fig.10 CLof Group 1vs.Ma

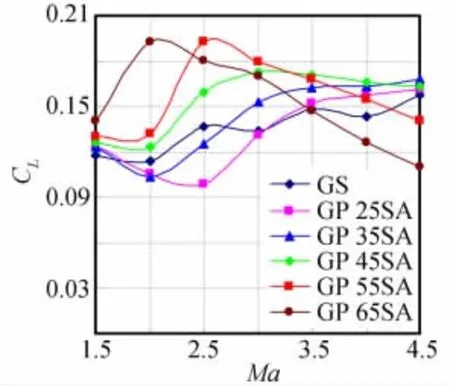
图11 第二组模型CL随Ma的变化Fig.11 CLof Group 2vs.Ma

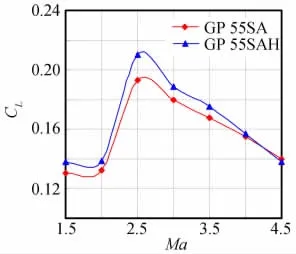
图12 第三组模型CL随Ma的变化Fig.12 CLof Group 3vs.Ma

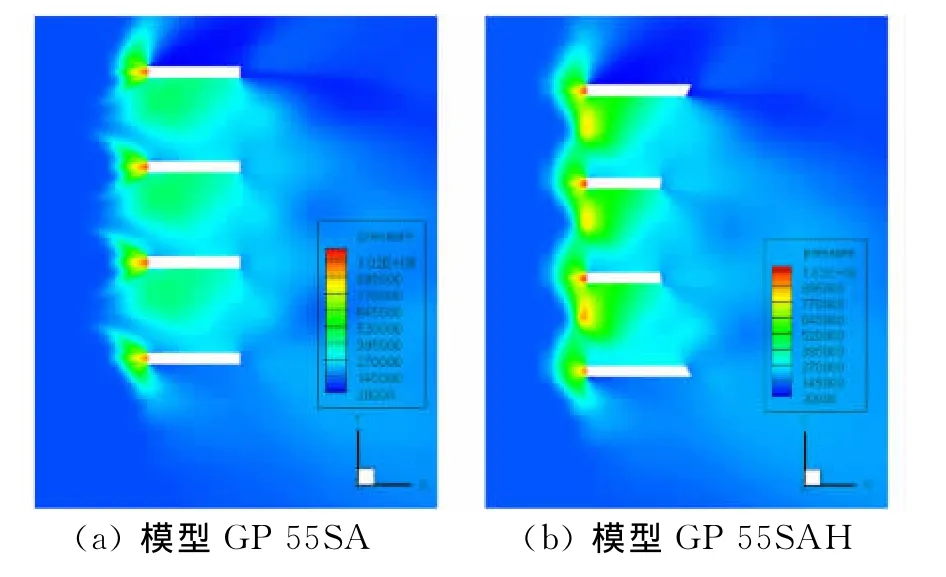
图13 贴体型前缘后掠式栅格翼模型压强分布图（截面Z）Fig.13 Pressure distribution of curve leeward gird fins（Section Z）

第一组模型的升阻比κ随马赫数的变化曲线如图14，在前缘不同后掠方式栅格翼模型的研究中，模型GP55SA和模型GV55SA由于后掠方式的不同，随马赫数的增加表现出了不同的升阻比规律，在Ma＜2时升阻比基本相同，均比无后掠模型GS大33.8%～62.5%，当Ma＞2后和模型GV 55SA比较而言，模型GP 55SA逐渐占优，并在此后随马赫数增加对模型GV 55SA保持18.2%～33.1%的优势。图15为第二组模型的升阻比κ随马赫数的变化曲线，可见随前缘后掠角度的增加，模型升阻比的变化呈现有序的规律性。

后掠角度的增大可有效改善栅格内部的气流壅塞现象，但需要看到的是在此同时也增大了栅格翼的最大弦长，在设计中需要综合考虑栅格翼升阻比及安装空间的限制，有意思的是φ1＝55°、65°这两个模型，到Ma＝4.5时两者的升阻比相同，说明在升阻比方面，栅格翼的前缘后掠角并非越大越好。

第三组模型的升阻比κ随马赫数的变化曲线如图16，模型GP 55SAH在所研究马赫数阶段都显示出了比模型GP 55SA更好的升阻比特性，联系图7和图12可知，前者的升力特性是获得升阻比优势的主导因素，说明对于前缘后掠式栅格翼，对安装面进行贴体型的设计不会影响其升阻特性，甚至还能获得略大的升力优势。

图17～图19为3组模型的压心系数Xcp随马赫数的变化曲线，因为对俯仰力矩采用统一的参考长度，由图可见和前缘无后掠模型相比较，前缘后掠模型的压心在后移的同时，随着后掠角度的增加，当φ1≥55°后，Ma＝2.5时不再出现压心前移现象。再次说明一定角度的前缘后掠减小了迎风面激波强度，能有效改善栅格内部的气流壅塞。

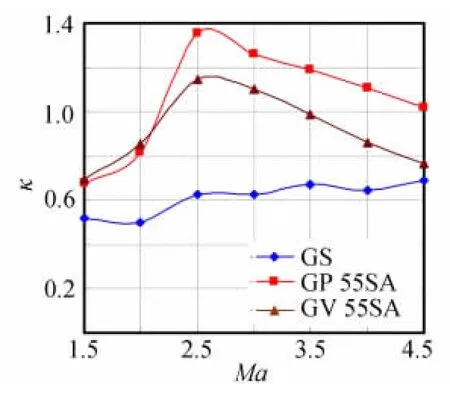
图14 第一组模型κ随Ma的变化Fig.14 κof Group 1vs.Ma

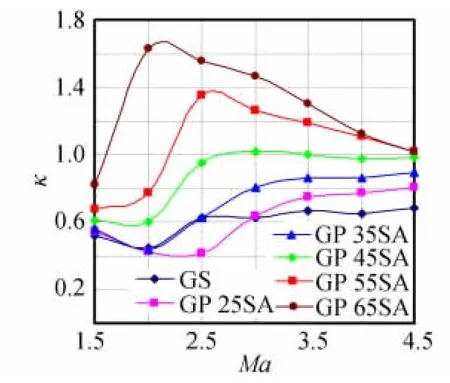
图15 第二组模型κ随Ma的变化 Fig.15 κof Group 2vs.Ma

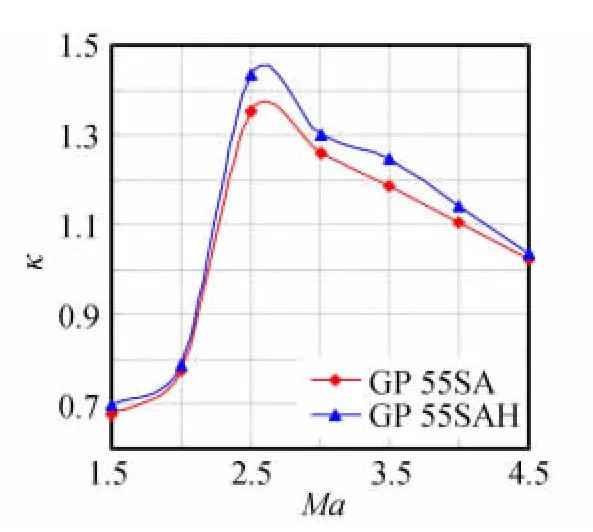
图16 第三组模型κ随Ma的变化 Fig.16 κof Group 3vs.Ma

图17 第一组模型Xcp随Ma的变化Fig.17 Xcpof Group 1vs.Ma

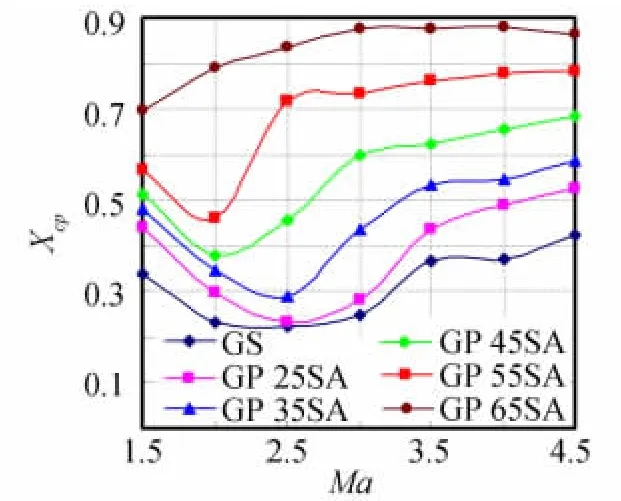
图18 第二组模型Xcp随Ma的变化 Fig.18 Xcpof Group 2vs.Ma

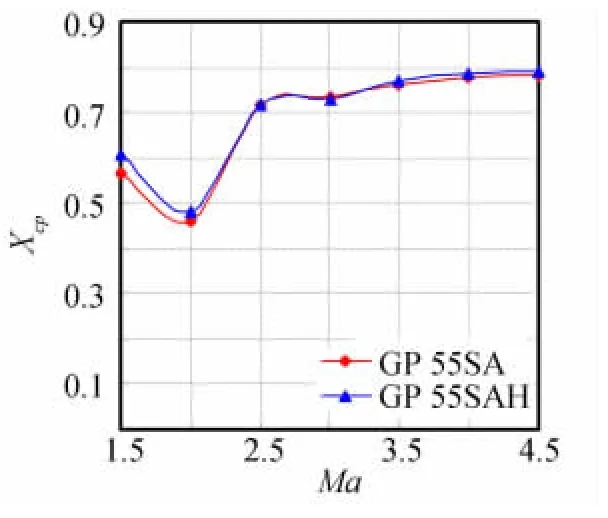
图19 第三组模型Xcp随Ma的变化 Fig.19 Xcpof Group 3vs.Ma

4 结 论

（1）采用栅格翼前缘后掠的方法，能有效减小栅格翼迎风面所产生的波阻，提高其升阻比，在所研究的马赫数范围内升阻比最大能提高116%，是一种新的栅格翼减阻增升设计方法。

（2）在不同的后掠方式中，相对于栅格边框中心为尖点的后掠方式而言，栅格格间交接点为尖点的后掠方式在升力特性和阻力特性方面表现更优，在所研究的马赫数范围内这种优势随马赫数的增加而增长，最大升阻比比前者大33.1%。

（3）随着后掠角度的增加，除φ1＝25°的模型在Ma＝2.5大于前缘无后掠栅格翼以外，栅格翼的波阻逐渐减小；升力系数随后掠角的增加在Ma＝2.5前后逐渐增大，说明前缘后掠能有效改善栅格内部的气流壅塞现象，值得注意的是在φ1≥55°随马赫数的增加升力系数开始减小，说明升力特性并非随前缘的后掠角度呈线性增长趋势。

（4）和前缘无后掠的栅格翼相比较，随后掠角度的增大，栅格翼的压心逐渐后移，同时在Ma＝2.5左右因为气流壅塞造成的栅格翼压心前移现象随后掠角的增加也逐渐消失，到φ1≥55°后栅格翼的压心随马赫数的增大而一致后移。

（5）在栅格翼的安装设计时，采用栅格翼背风面带一定弧度的贴体型设计不会影响到栅格翼的升阻特性，在所研究的模型中，升阻比还有部分提高，最大增长率为5.8%。

［1］MILLER M S，WASHINGTON W M D.An experimental investigation of grid fin drag reduction techniques［R］.AIAA－CP－94－1914，1994.

［2］陈少松，徐琴，王福华，等.格栅翼减阻特性研究［J］.流体力学实验与测量，2001，15（4）：7－11.

［3］THEERTHAMALAI P，BALAKRISHNAN N.Effect of geometric parameters on the aerodynamic characteristics of grid－fin cells at supersonic speeds［R］.AIAA 2007－690，2007.

［4］雷娟棉，吴小胜，吴甲生.格栅尾翼（舵）外形参数对气动特性的影响［J］.北京理工大学学报，2007，27（8）：675－679.

［5］吴小胜，雷娟棉，吴甲生.格栅翼外形参数对气动特性影响的数值计算研究［J］.兵工学报，2007，28（12）：1468－1472.

［6］CAI Jin－sheng.Numerical study on choked flow over grid－fin configurations［J］.Journal of Spacecraft and Rockets，2009，46（5）：949－956.

［7］ZENG Yan，CAI Jin－sheng，DEBIASI M，et al.Numerical study on drag reduction for grid－fin configurations［R］.AIAA 2009－1105，2009.

［8］BERNER C，DUPUIS A.Wind tunnel tests of a grid finned projectile configuration［R］.AIAA 2000－0105，2001.