与函数类有关的积分表示和卷积性质

彭 娟,刘文娟,杨 清

(扬州大学 数学科学学院,江苏 扬州 225002)

彭 娟,刘文娟,杨 清

(扬州大学 数学科学学院,江苏 扬州 225002)

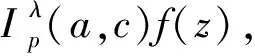
亚纯函数; 微分从属; 卷积; 积分表示

0 引言

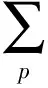
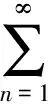
(1)

且在去心单位圆U*={z:z∈C,0lt;|z|lt;1}=U{0}内p叶解析的函数f(z)组成的函数类.

我们定义如下函数φp(a,c;z):

(2)

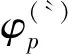
(3)

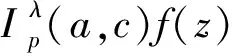
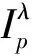
(4)

从(1)和(4)可看出,

(5)

由(5)有

(6)

(7)

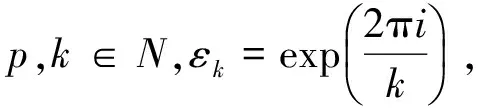
(8)

定义1 设f(z)∈Σp,若满足从属条件

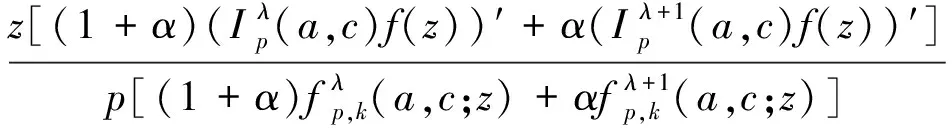
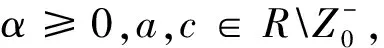
特别地∂=0,有

为了证明主要的结论,我们需要以下的引理.

引理1[10]设β,γ∈C,h(z)在U内解析,凸单叶,并且

h(0)=1,R(βh(z)+γ)gt;0(z∈U).

如果p(z)在U内解析,p(0)=1,若满足

则

p(z)h(z)(z∈U).

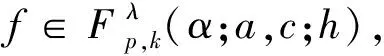
(9)

进一步地,若

则

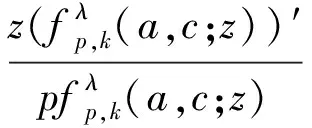
证明由

(10)

(11)

则

(12)

令

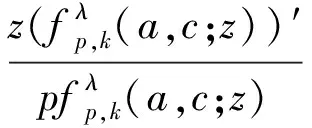
(13)

(14)

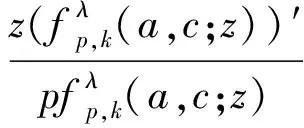
1 主要结果

(15)

其中ω(z)在U内解析,ω(0)=0,|ω(z)|lt;1(z∈U).

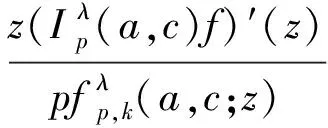
(16)

其中ω(z)在U内解析,ω(0)=0,|ω(z)|lt;1(z∈U).

(17)

(18)

对(18)两边积分有

(19)

则

(20)

其中ω(z)在U内解析,ω(0)=0,|ω(z)|lt;1(z∈U).

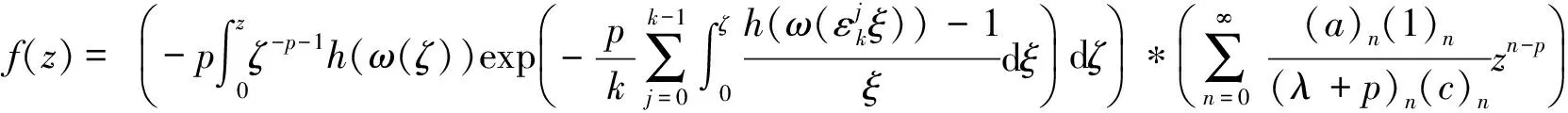
其中ω(z)在U内解析,ω(0)=0,|ω(z)|lt;1(z∈U).

(21)

其中ωj(z)(j=1,2)在U内解析,ωj(0)=0,|ωj(z)|lt;1(z∈U;j=1,2).

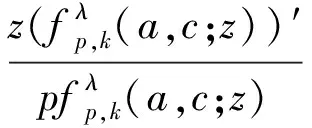
(22)

其中ω1(z)在U内解析,ω1(0)=0,|ω1(z)|lt;1(z∈U).

(23)

(24)

其中ωj(z)(j=1,2)在U内解析,ωj(0)=0,|ωj(z)|lt;1(z∈U;j=1,2).

对(24)两边积分有

其中ω(z)在U内解析,ω(0)=0,|ω(z)|lt;1(z∈U).

致谢作者感谢刘金林老师的悉心指导!

[1]Aouf M K,Silverman H,Srivastava H M. Some families of linear operators associated with certain subclasses of multivalent functions[J]. Appl Math Comput,2008,55:535-549.

[2]Aouf M K. Certain subclasses of meromorphically multivalent functions associated with generalized hypergeometric function[J]. Appl Math Comput,2008,55:494-509.

[3]Cho N E,Kwon O S,Srivastava H M. Inclusion relationships and argument properties for certain subclasses of multivalent functions associated with a family of linear operators[J]. J Math Anal Appl,2004,292:470-483.

[4]Cho N E,kim Y C,Srivastava H M. Argument estimates for a certain class of analytic functions[J]. Complex Variables,38:277-287.

[5]Liu J L,Patel J. Certain properties of multivalent functions associated with an extended fractional differintegral operator[J]. Appl Math Comput,2008,203:703-713.

[6]Liu J L. Some properties of certain meromorphically multivalent functions[J]. Appl Math Comput,2009,210:136-140.

[7]Liu J L,Srivastava H M. Class of meromorphically multivalent functions associated with the generalized hypergeometric function[J]. Math Comput Modelling,2004,39:21-34.

[8]Liu J L,Srivastava H M. A linear operator and associated families of meromorphically multivalent functions[J]. J Math Anal Appl,2001,259:566-581.

[9]Liu J L,Srivastava H M. A class of multivalently analytic functions associated with the Dziok-Srivastava operator[J]. Integral Transforms and Special Functions,2009,20(5):401-417.

[10]Miller S S,Mocanu P T. Differential subordinations and univalent functions[J]. Michigan Math J,1981,28:157-171.

[责任编辑：李春红]

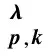
PENG Juan,LIU Wen-juan,YANG qing

(School of Mathematical Science,Yangzhou University,Yangzhou Jiangsu 225002,China)

meromorphic functions； differential subordination； integral representation； integral operator

O174.5

A

1671-6876(2012)01-0022-04

2011-12-12

彭娟(1986-),女,湖北洪湖人， 硕士研究生,研究方向为复分析.