基于颗粒-界面-基体模型圆形巷道围岩中应力与应变演变分析

王学滨，伍小林，潘一山，张春野

（辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000）

1 引 言

圆形巷道围岩的结构形式虽然简单，但其破坏形式却表现出多样性。在非静水压力条件下（侧压系数不等于 1），破坏后的巷道的形状通常为椭圆形，这是由于在围岩中形成了 2个相对的三角坑[1－5]。在三角坑的内部，有时可以观察到倾斜的剪切裂纹[3]，有时可以观察到与巷道表面基本平行的拉伸裂纹[4－5]，与后者有关的现象常称之为围岩的层裂或板裂化现象。在深部的巷道围岩中，会出现呈圆环形的破坏区与非破坏区相间隔的现象，这种现象常称之为分区破裂化现象[6－8]。另外，在巷道围岩中也可以观测到开挖扰动区或松动圈[9－10]。

圆形巷道围岩的不同破坏形式存在于多种工程领域之中，例如，采矿工程、交通隧道工程、防护工程、石油工程及水利水电工程等，因而圆形巷道围岩的破坏形式的研究及机制分析引起了众多研究人员的关注。文献[11]引入随围压而改变的弹性模量公式，解释了巷道围岩中的最大切应力位于巷道表面之后，而不是刚好位于表面上的原因，这可以在一定程度上解释与巷道表面平行的裂纹出现的原因，但这是基于线弹性的均质模型获得的结果。文献[12]基于各向异性损伤模型的研究发现，临近破坏时最大切向应力位于距巷道表面一定深度处，该研究结果较好地解释了岩爆剥落岩片存在一定厚度的现象。文献[1－2]基于前人提出的非均质材料模型，假设了两种能导致岩爆或突出的破坏形式：（1）颗粒和基体的韧度相差不多时的劈裂破坏；（2）颗粒的韧度远高于基体时的剪切破坏，该文献认为一些实验结果与这两种破坏模式非常一致，究竟发生哪种破坏关键取决于岩石的微结构。对于花岗岩，晶粒之间的缝隙被随机分布的胶结晶粒（与花岗岩的性质类似）填充，因而导致了劈裂型岩爆；对于石灰岩，颗粒比胶结材料的强度稍高，使裂纹不能沿最小阻力（垂直于3σ）方向扩展，迫使裂纹沿晶传递，与3σ成一定的角度，引起剪切型岩爆。基于上述观点及结果，可以认为微结构或细观结构在围岩的破坏形式方面起了关键的作用，不应该被忽视。

本文采用文献[13－14]中提出的以连续介质模型作为基础的颗粒-界面-基体模型，研究侧压系数及颗粒尺寸不同条件下开挖圆形巷道之后围岩中的一些力学量的分布规律，研究结果有利于进一步认识层裂、三角坑式破坏及分区破裂化等现象的机理，对于深部巷道围岩的破坏规律研究及稳定性控制或许具有积极的意义。

2 颗粒-界面-基体模型

本文中将岩石简化为具有不同力学属性的3种成分，即颗粒、界面和基体。

颗粒不发生破坏，而总保持为弹性状态，用于模拟岩石中通常不发生破坏的部分，例如，砂岩中的颗粒或被节理切割的高强度岩块。颗粒的形状假设为圆形，采用若干正方形单元模拟，单元的本构模型取为各向同性的线弹性材料，弹性模量和泊松比分别取26.52 GPa和0.21。

界面用于模拟颗粒之间的错动、压缩及拉伸行为。界面的形状为矩形，也采用若干正方形单元模拟（尺寸与颗粒单元的相同）。界面单元在发生破坏之前，其本构模型与颗粒单元的并无差别，而在破坏之后，其承载能力不再发生改变，本构模型取为摩尔-库仑准则，由于该准则通常会高估抗拉强度，因此需要对其进行拉伸截断。黏聚力、内摩擦角及抗拉强度分别取为2 MPa、30°及1 MPa。

除了界面和颗粒之外的物质是基体，用于模拟强度较低的充填体，即模拟碎屑、杂质、孔隙的一个综合效果。基体也被剖分成与颗粒和界面单元相同尺寸的若干正方形单元，其本构模型与界面的相同，但一些参数有所降低。基体单元的弹性模量、黏聚力、内摩擦角及抗拉强度均被降低到界面单元的 25%，而泊松比并不改变。文献[15]在静水压力条件下，研究了基体单元的一些力学参数下降到界面单元的75%～0.1%过程中围岩应力、应变的分布规律，并与经典的均质模型的结果进行了比较，研究发现，降低到界面单元的25%时的结果较好，因此，本文以此作为基础进行计算。

本文中，颗粒-界面-基体模型尺寸为1 000 mm×1 000 mm，共计被剖分成500×500个正方形单元，正方形单元的边长为2 mm。计算中，采用6个计算方案，如图1所示，图中黑色、灰色、白色区域分别代表界面、颗粒和基体，中间的巷道是在计算步骤第二阶段开挖的。

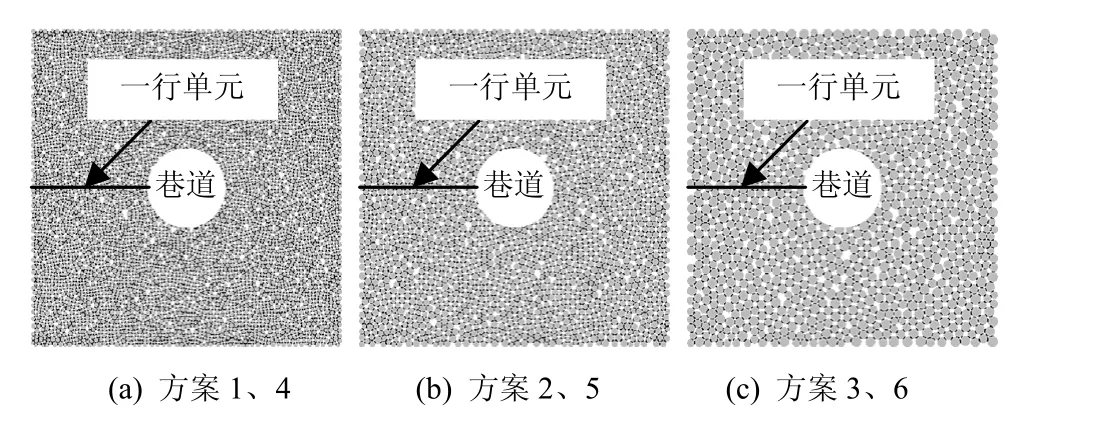
图1 不同粒径的颗粒体模型Fig.1 The granular model with different radii

对于前方案1～3，在静水压力条件下计算，模型四周的压应力均为3.0 MPa，但颗粒的平均直径有所不同。3个方案中颗粒最大直径分别为17.5、24.5、34.3 mm，最小直径分别为12.5、17.5、24.5 mm。每个方案中，颗粒的直径满足均匀的随机分布规律，目前尚无法开展基于真实颗粒尺寸的巷道围岩中应力、应变的计算工作。

方案4～6在侧压系数等于0.5条件下计算，模型上、下两面的压应力为3.0 MPa，而模型左、右两面的压应力为1.5 MPa，其中颗粒的排列方式及尺寸分别同方案1～3。

开挖巷道之前，方案 1～3中的颗粒的数目分别为4 547、2 329、1 197个，颗粒单元的数目分别为166 151、179 963、187 797个，界面单元的数目分别为43 087、26 190、15 826个。基体单元的数目也可以根据上述数目及正方形单元总数确定出来，方案 1～3中的基体单元的数目占单元总数的百分比分别约为16.3%、17.5%、18.6%。

颗粒的堆积方式需要利用一定的算法，本文中模拟了颗粒在重力作用下的自然堆积过程，其详细过程参见文献[14]。如果2个颗粒被判为发生接触，则需要在它们之间规定一个可以模拟接触的较薄的矩形界面，与界面有关的参数（如界面的长度、宽度及位置）的计算公式见文献[16]。

在小变形及平面应变条件下数值计算分3步：

第一步：采用初始化模型中各个单元各个方向应力的方法给单元的应力赋予初值，并在模型的四周施加压力，使受载的模型尽早达到静力平衡状态。当模型中节点的最大失衡力小于0.05 N时，认为模型已达到了静力平衡状态。

第二步：通过调用编写的FISH函数[13－16]，在模型中开挖圆形的巷道，直径为 250 mm。为了使巷道的表面看起来更圆，将直径范围内的单元一律删除。在此过程中，有些颗粒或界面也能被切开，这不会对计算结果产生大的影响，但实现起来却非常方便，而且效果美观。

第三步：重新开始计算，直到30 000个时步，此时各方案的最大失衡力已经足够小，可以认为均达到了静力平衡状态。

3 计算结果

3.1 图例说明

图 2(a)～2(e)给出了巷道围岩中的剪切应变增量分布的等值线图，超过3×10-4的剪切应变增量用白色区域显示，它们的位置紧挨着巷道表面，其余的部分，用灰度表示值的大小，颜色越黑代表值越大。在图3、4中(a)～(e)及图5(a)～5(c)中也类似，不再赘述。图 2(a)～2(c)是方案 1的结果，时步分别为 5 000、10 000、30 000；图 2(d)～2(e)分别是方案2、3的结果，时步均为30 000。图3、4中(a)～(e)分别给出了最小及最大主应力的分布规律，图3(a)～3(e)只显示了-8～0 MPa之间的最小主应力，即只显示了较高的最小主应力，负号代表压缩；图4(a)～4(e)只显示了0～0.8 MPa之间的最大主应力，即只显示较高的最大主应力，正号代表拉伸）。图3、4中(a)～(e)图超过上述范围的最小及最大主应力用白色区域显示，这与图2(a)～2(e)类似。图5给出了方案4的计算结果，时步为30 000。

图2 方案1～3的剪切应变增量高值区的分布规律Fig.2 The distribution of the shear strain increment in schemes 1 to 3

图3 方案1～3的最小主应力的负高值区的分布规律Fig.3 The distribution of the minor principal stress in schemes 1 to 3

图4 方案1～3的最大主应力的正高值区的分布规律Fig.4 The distribution of the maximum principal stress in schemes 1 to 3

图5 方案4的计算结果（30 000时步）Fig.5 Calculated results in schemes 4 (30 000 timesteps)

图2～4的(f)图分别为图2～4中(c)图位于巷道右侧围岩中的一小块区域的局部放大图，颜色越黑代表值越大，在这些图中也给出了颗粒、界面及基体的具体位置，分别显示为白色、黑色和灰色。在图2～4的(f)图中，紧挨着巷道表面的位置，有时能观察到岩石的细观结构，这些位置的值很高，剪切应变增量比3×10-4大，最小主应力的值比8.0 MPa大，最大主应力比0.8MPa大。

3.2 剪切带网络

由图2可以发现，剪切应变增量的高值区呈弯曲的条带状展布，它们最初起源于巷道的表面上，然后向围岩的深部传递。离巷道表面越近，剪切应变增量的值越高；在远离巷道表面的位置，剪切应变增量的值较小，几乎不受巷道开挖的影响。这些条带状的剪切应变增量的高值区有的沿顺时针转向向远处传递，而有的则沿逆时针转向，它们彼此交叉，形成了离巷道表面越远越稀疏的网状的图案，如同塑形力学中的滑移线网。为表述方便，可以将这些弯曲的条带状的剪切应变增量的高值区称之为剪切带。从整体上看，大量的相互交织的剪切带形成了一个位于巷道围岩中的呈圆环形的剪切应变集中区域，这与巷道开挖之后形成的扰动区或松动圈[9－10]的形态比较类似。

随着时步的增加（从5 000时步至10 000时步再到30 000时步），呈圆环形的剪切应变集中区域内部的剪切带的长度有所增加，见图2(a)～2(c)。这说明巷道开挖之后，围岩中一些位置的应力还在不断地增加和调整，围岩尚未达到静力平衡状态。由计算结果可以发现，当超过30 000时步时，围岩中的剪切应变增量的分布规律基本上不再发生改变，表明围岩已经达到了静力平衡状态。

比较关心剪切带的传播路径，即剪切带的位置与颗粒、界面及基体位置之间的关系。由图 2(f)可以发现，在巷道表面附近，颗粒、界面及基体中的剪切应变增量都较高，但基体中的最高。这一结果是合理的，因为基体的强度最低，因而可以积累更高的剪切应变增量。在离巷道表面稍远处，基体和界面处的剪切应变增量都较高，而颗粒处的值较低。在离巷道表面更远处，只有基体位置的剪切应变增量较高。上述计算结果与文献[1－2]中裂纹沿晶粒的边界穿行的观点和结果类似。

3.3 最小主应力的分布

图3的结果表明，最小主应力的负高值区呈若干圆环形分布在巷道的围岩中，离巷道表面越近，最小主应力的值越高，圆环之间的间距越小，以致于很难区分它们，尤其是当颗粒的尺寸较小时。离巷道表面较远处的圆环之间的间距显得更大。由于界面单元很少，而且基体本来就比较弱，因而最小主应力的高值区主要位于颗粒位置，若干颗粒通过自组织作用在环向的高压应力条件下彼此挤压在一起，进而形成呈圆环形的最小主应力的高值区，这一点可从图3(f)中看出。

3.4 最大主应力的分布

由图4可以发现，最大主应力的正高值区位于巷道围岩的径向。在巷道表面附近，最大主应力基本为正值，其原因是由于在高的环向压应力作用下颗粒之间发生了复杂的运动和变形所致，基于传统的数值模型和理论模型并不能得到这样的结果。文献[17]基于含缺陷的岩体结构模型的研究结果表明，在卸载情况下，岩石中将在缺陷处形成平行于卸载方向的拉应力，本文的计算就是在“先加载，后挖洞”（即卸载）条件下进行的。

3.5 监测单元的3种量的分布及演变

以方案1为例，研究了一行监测单元在不同时步时3种量（剪切应变增量、最小及最大主应力）的分布及演变规律，如图 6(a)～6(c)所示。这行被监测单元的位置见图 1。为了明确地看出不同类型单元上的上述3种量的分布及演变规律，图6中也标明了这3种单元的分布情况，采用3种不同高度上的线段进行标明，最上方的是颗粒单元，中间的是界面单元，最下方的是基体单元。这些不同高度的线段的纵坐标的值并没有什么意义。

由图 6(a)可见，（1）在离巷道表面大约 1.5倍半径的范围之内，围岩中的剪切应变增量较高，而在远处，其值基本不变；（2）在大约1.5倍半径之内，剪切应变增量曲线的下限保持较好的单调性，但在多处位置，剪切应变增量的值明显较高，因而剪切应变增量曲线呈现出了较大的波动性，这些剪切应变增量偏高的位置恰好位于基体位置，这与图2(a)～2(c)和图 2(f)反映的规律是一致的；（3）随着时步的增加，剪切应变增量的值有所提高，直到当时步达到30 000时，其值基本不再发生改变。由图6(b)可以发现，最小主应力的负高值区的位置位于颗粒的边缘处或位于界面处，这与基体强度低有关，基体单元不能承受较高的环向压应力，因而其最小主应力被分担在了另外的两种单元上，这与图3(a)～3(c)和图 3(f)反映的规律类似。由图 6(c)可以发现，最大主应力的高值区分布在基体上，在巷道表面附近，最大主应力出现了较高的正值，代表径向受拉，这与图 4(a)～4(c)和图 4(f)反映的规律类似。

图6 方案1的一行监测单元的3种量的分布规律Fig.6 Distributions of three quantities at a row of monitored elements in scheme 1

图 6(a)～6(c)表明，不同时步时 3种量的曲线的分布规律具有一定的类似性，这显然是受围岩中3种成分分布的影响。

4 颗粒尺寸及侧压系数的影响分析

4.1 颗粒尺寸的影响及一种可能的分区裂化机制

图 2(c)～2(e)的结果表明，随着颗粒尺寸的增加，剪切带的数目有所降低，长度有所增加，剪切带显得更加粗壮，因而位于巷道周围的呈圆环形的剪切应变集中区域的尺寸有所增加。通过计算还可以发现，方案 1～3的最高剪切应变增量分别为2.016 1× 10-3、2.685 4×10-3、2.0011×10-3，随着颗粒尺寸的增加，最高剪切应变增量并不单调地增加，这是由于在颗粒的平均直径增加时，颗粒的排列方式也发生了变化。

图 3(c)～3(e)的结果亦表明，随着颗粒尺寸的增加，最小主应力负高值区的数量（圈数）有所降低，范围有所增加，看起来并不很圆，圆环之间的间距有所增加，且每条圆环的厚度也有所增加。通过计算还可以发现，方案 1～3的最小主应力最高分别可达-9.2、-11.1、-11.3 MPa（负号代表压缩），因此该值随着颗粒尺寸的增加而增加。

图 4(c)～4(e)的结果表明，随着颗粒尺寸的增加，最大主应力的正高值区的数量（圈数）有所减少，其延伸范围有所增加，其厚度有所增加。通过计算还可以发现，方案 1～3的最大主应力最高分别可达 1.4、1.6、1.9 MPa（正值代表拉伸），该值随着颗粒尺寸的增加而增加。

与图 3(a)～3(b)相比，图 3(c)的结果与分区破裂化的现场观测结果[6－7]更吻合。据此，本文对分区破裂化的一种可能机制推测为：分区破裂化现象可以形成于节理岩体之中（文献[18]在数值模拟研究中也考虑了一套节理的存在）。由于自组织作用，若干被节理切割的岩块在环向的受高压应力作用下彼此挤压在一起，一旦超过了岩石的抗压强度，就会发生破坏或劈裂，进而形成一条破裂区，这一条破裂区的位置显然不应位于巷道的表面上，而是与巷道的表面有一定的距离。而且，围岩中的应力水平如果足够高，这样的破裂区可能出现多条，这样就形成了分区破裂化现象。本文中的颗粒就相当于岩块，而界面和基体就在某种程度上代表了节理。

显然，本文中对分区破裂化机制的解释不同于以往的文献，强调了岩体的结构和自组织作用，不需要“伪掌子面”的不断形成假定[6－7]及塑性滑移线或破坏特征线[19]等概念，也不需要引入其他的理论，诸如梯度模型[20－21]、相变模型[21－22]及非欧模型[22]等。但是，本文方法与这些模型之间也有共性，即都从不同的角度考虑了材料变形的非协调性（相变模型及非欧模型）或微结构的相互作用（梯度模型）。不过，本文的颗粒模型将这些特点综合考虑在一起，颗粒之间必然存在一定的相互影响和作用，颗粒之间的运动在一定程度上导致了变形的非协调性。在节理岩体中，由于节理的存在，会导致变形的非协调性。上述不同于传统的连续介质的行为及自组织作用，应该是分区破裂化现象的可能原因之一。

上述研究是在二维条件下得到的结果。在三维条件下，基于连续介质模型也可以得到类似分区破裂化的结果[23]，分区破裂化现象被认为是空间局部化现象，由若干呈锥面分布的空间剪切带形成的。

通过计算发现，方案4～6的剪切应变 增量最高分别可达 1.375 0× 10-3、1.865 8× 10-3、2.021 2 ×10-3；最小主应力最高分别可达-10.8、-15.2、-12.1 MPa；最大主应力最高分别可达1.3、1.8、1.9 MPa。随着颗粒尺寸的增加，如果围岩中的应力、应变的最高值增加，这是易于理解的，因为方案4～6中软弱的基体单元的数目占单元总数的百分比越来越高。但是，有时会有例外的情况发生，这只能从颗粒的排列方式发生了改变进行解释。

4.2 侧压系数的影响

由图 5(a)～5(b)可以发现，当侧压系数为 0.5时，巷道两帮的剪切应变增量及最小主应力的值明显较高，应力、应变集中区大致呈三角形。在三角形之内，可以观察到若干相互交织的剪切带和呈条带状的最小主应力的高值区。这两个三角形区域的岩石如果发生剥落，则破坏后的巷道将呈椭圆形，这与许多实际测量结果[1－5]相吻合。由图5(c)可以发现，在巷道的两侧及顶、底部，最大主应力的正高值区的分布规律并没有太大的差别。但是，经过仔细观察可以发现，巷道顶、底部的最大主应力确实要稍高一些，这与侧压系数为0.5有关。

5 结 论

（1）颗粒-界面-基体模型的计算结果表明，圆形巷道开挖之后，围岩中的剪切应变增量的高值区主要集中在较弱的基体之中，而最小主应力的高值区（环向高受压区）主要分布在弹性的颗粒之中。圆形巷道周围的应力、应变集中区或开挖扰动区的轮廓依赖于侧压系数。

（2）平均颗粒尺寸的增加，使剪切带的数目降低，长度增加，最小主应力的高值区的圈数降低，间距增加。平均颗粒尺寸大时的计算结果与深部岩石分区破裂化现象具有一定的类似性，由此提出裂化的一种可能的机制。

[1] HAIMSON B C, SONG I.Laboratory study of borehole breakouts in Cordova Cream: A case of shear failure mechanism[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(7): 1047－1056.

[2] SANTARELLI F J, BROWN E T.Failure of three sedimentary rocks in triaxial and hollow cylinder compression tests[J].International Journal of Rock Mechanics and Mining Sciences& Geomechanics Abstracts, 1989, 26(5): 401－413.

[3] EWY R T, COOK N G W.Deformation and fracture around cylindrical openings in rock——II.Initiation,growth and interaction of fractures[J].International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts, 1990, 27: 409－427.

[4] MARTIN C D.The effect of cohesion loss and stress path on brittle rock strength[J].Canadian Geotechnical Journal, 1997, 34(5): 698－725.

[5] BAZANT Z P, LIN F B, LIPPMANN H.Fracture energy release and size effect in borehole breakout[J].International Journal for Numerical and Analytical Methods in Geomechanics, 1993, 17(1): 1－14.

[6] SHEMYAKIN E I, FISENKO G L, KURLENYA M V,et al.Zonal disintegration of rocks around underground workings.Part I.Data of in-situ observation[J].Journal of Mining Science, 1986, 22(3): 157－168.

[7] SHEMYAKIN E I, FISENKO G L, KURLENYA M V,et al.Zonal disintegration of rocks around underground workings.Part III.Theoretical concepts[J].Journal of Mining Science, 1987, 23(1): 1－6.

[8] 周小平, 钱七虎.深埋巷道分区碎裂化机制[J].岩石力学与工程学报, 2007, 26(5): 878－885.ZHOU Xiao-ping, QIAN Qi-hu.Zonal fracturing mechanism in deep tunnel[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 878－885.

[9] 董方庭, 宋宏伟, 郭志宏, 等.巷道围岩松动圈支护理论[J].煤炭学报, 1994, 19(1): 21－32.DONG Fang-ting, SONG Hong-wei, GUO Zhi-hong, et al.Roadway support theory based on broken rock zone[J].Journal of China Coal Society, 1994, 19(1): 21－32.

[10] 靖洪文, 付国彬, 郭志宏.深井巷道围岩松动圈影响因素实测分析及控制技术研究[J].岩石力学与工程学报,1999, 18(1): 70－74.JING Hong-wen, FU Guo-bin, GUO Zhi-hong.Measurement and analysis of influential factors of broken zone of deep roadways and study on its control technique[J].Chinese Journal of Rock Mechanics and Engineering, 1999, 18(1): 70－74.

[11] SANTARELLI F J, BROWN E T, MAURY V.Analysis of borehole stress using pressure dependent linear elasticity[J].International Journal of Rock Mechanics and Mining Sciences, 1986, 23(6): 445－449.

[12] 祝方才, 潘长良, 曹平.基于各向异性损伤的厚壁筒应力分布有限元分析[J].岩石力学与工程学报, 2003,22(5): 838－842.ZHU Fang-cai, PAN Chang-liang, CAO Ping.Stresses analysis of surrounding rocks based on thick cylinder and anisotropic damage theory by finite element method[J].Chinese Journal of Rock Mechanics and Engineering,2003, 22(5): 838－842.

[13] 伍小林, 王学滨, 潘一山.单向压缩条件下圆形颗粒体含孔洞试样的力学模拟[J].水利水运工程学报, 2010,31(3): 40－44.WU Xiao-lin, WANG Xue-bin, PAN Yi-shan.Numerical simulation of mechanical behavior of a specimen composed of circular granular material[J].Hydro-Science and Engineering, 2010, 31(3): 40－44.

[14] 伍小林, 王学滨, 潘一山.含不同半径孔洞的颗粒体模型的力学行为数值模拟[J].中国地质灾害与防治学报,2011, 22(1): 107－114.WU Xiao-lin, WANG Xue-bin, PAN Yi-shan.Numerical simulation of mechanical behavior of the granular model with holes with different radii[J].The Chinese Journal of Geological Hazard and Control, 2011, 22(1): 107－114.

[15] 伍小林, 王学滨, 潘一山.基于两种颗粒体模型的巷道围岩应力、应变分布的研究[J].中国地质灾害与防治学报, 2011, 22(4): 56－62.WU Xiao-lin, WANG Xue-bin, PAN Yi-shan.Study of the stress and strain in surrounding rock of the tunnel based on two kinds of granular models[J].The Chinese Journal of Geological Hazard and Control, 2011, 22(4):56－62.

[16] 王学滨, 伍小林, 潘一山.圆形巷道围岩层裂的等效连续介质模型及侧压系数的影响[J].岩土力学, (待刊).WANG Xue-bin, WU Xiao-lin, PAN Yi-shan.An equivalent continuum model for the exfoliationphenomenon of surrounding rock of a circular tunnel and effects of lateral confining pressure coefficients[J].Rock and Soil Mechanics, in press.

[17] 王明洋, 范鹏贤, 李文培.岩石的劈裂和卸载破坏机制[J].岩石力学与工程学报, 2010, 29(2): 234－241.WANG Ming-yang, FAN Peng-xian, LI Wen-pei.Mechanism of splitting and unloading failure of rock[J].Chinese Journal of Rock Mechanics and Engineering,2010, 29(2): 234－241.

[18] ZHOU X P, WANG F H, QIAN Q H, et al.Zonal fracturing mechanism in deep crack-weakened rock masses[J].Theoretical and Applied Fracture Mechanics, 2008, 50: 57－65.

[19] CHANYSHEV A I.深部围岩的塑性变形及分区破裂化现象[C]//深部岩石工程围岩分区破裂化效应.北京:中国科学技术出版社, 2008: 95－108.CHANYSHEV A I.Phenomenon of zonal disintegration and plastic deformation of the deep surrounding rock[C]//Effects of Zonal Disintegration of the Surrounding Rock in Rock Engineering at Depth.Beijing: China Science and Technology Press, 2008: 95－108.

[20] WANG M Y, QI C Z, QIAN Q H et al.One plastic gradient model of zonal disintegration of rock mass near deep level tunnels[J].Journal of Mining Science, in press.

[21] QI C Z, QIAN Q H, WANG M Y.Evolution of the deformation and fracturing in rock masses near deep-level tunnels[J].Journal of Mining Science, 2009, 45(2): 112－119.

[22] 戚承志, 钱七虎, 王明洋, 等.分区破裂化现象的研究进展[J].解放军理工大学学报(自然科学版), 2011,12(5): 472－479.QI Cheng-zhi, QIAN Qi-hu, WANG Ming-yang, et al.Advance in investigation of zonal disintegration phenomenon[J].Journal of PLA University of Science and Technology (Natural Science Edition), 2011, 12(5):472－479.

[23] 王学滨, 潘一山, 张智慧.基于加荷和卸荷模型的分区破裂化初步模拟及空间局部化机理[J].辽宁工程技术大学学报(自然科学版), 2012, 31(1): 1－7.WANG Xue-bin, PAN Yi-shan, ZHANG Zhi-hui.Preliminarily numerical simulation of the zonal disintegration phenomenon based on loading and unloading models and the mechanism of spatial strain localization[J]. Journal of Liaoning Technical University (Natural Science), 2012, 31(1): 1－7.