深部巷道围岩变形破坏机制分析

李 杰，宋春明，胡 啸，陈文涛，范鹏贤

(1.解放军理工大学 爆炸冲击防震防灾国家重点实验室，南京 210007；2.空军工程环境质量站，北京 102208)

1 引 言

随着工程的埋深增加和规模加大，目前在深地下工程的设计和施工过程中遇到了一些共同的难题[1－5]，例如，采用何种支护方法提高围岩稳定性，如何避免能量突然释放引起的岩爆等等，要回答这些问题，必须对高地应力条件下深部岩体的变形破坏特性与破坏准则进行详细的探讨。

20世纪80年代初，国外就已经开始针对深部矿井问题进行专题研究。由于岩石工程不断向深地下发展，一些国家和地区，尤其有深井矿山的国家，美国、俄罗斯、加拿大、澳大利亚、南非，波兰等都集中人力物力，针对深部开采等相关技术以及基础问题等展开了深入的研究，取得了巨大的进展[6－7]。

对于深部问题的研究我国虽然起步较晚，但在钱七虎院士等的大力倡导下[8]，我国学者也对深部岩体力学等进行了富有成效的研究，一些科学家对深部岩体的特征科学现象（分区破裂化、冲击地压、超低摩擦、岩体的低频准共振现象等）提出了一系列独到的观点，在岩体的结构层次及其形成机制、力学性质的关系、深部岩体的变形与运动特性方面取得了阶段性的成果[9－11]，如周小平等[12－13]利用弹性力学理论，得到了在原岩应力及开挖扰动作用下巷道围岩的弹性应力场及位移场，认为当弹性应力场满足破裂条件时岩体发生破裂，形成破碎区。戚承志等[14]利用连续相变理论，研究了巷道围岩的分区破裂化现象。冯夏庭等[15]在锦屏II级水电站工程实践的基础上，根据支护要求和控制因素将深埋硬岩隧洞的破坏现象详细分类，分析各种破坏模式（重点讨论岩爆）的发生机制、表现形态以及调控策略等等。

本文在已有研究的基础上，采用弹脆性本构模型对深部围岩应力分布以及变形破坏机理进行分析，对深部围岩支护以及分区破裂化现象机理阐述等都具有一定的意义。

2 数学计算模型

为便于分析，探讨圆截面水平坑道的开挖问题，如图1所示，将问题看作平面应变问题，在极坐标（r,θ）下平衡微分方程及几何方程分别为[16]：

式中：σr、σθ分别为径向和环向应力；εr、εθ为径向和环向应变；ur为径向位移；γrθ为剪切应变。

坑道掘进时，巷道周围岩体中发生应力重新分布，其初始状态为静水压力(取柱坐标)：式中：γ0为重度；H为巷道埋深；σr、σθ、σz的上标0表示初始应力。

平面应变条件下坑道附近的应力分布通常如图1所示。图中， ri为开挖半径；rc为不可恢复区半径；pi为支撑压力；σθmax为峰值支撑压力，这能在大量实验中得到，用弹塑性介质或具有摩擦力的介质模型计算能得到同样的应力分布图。

在有支承压力 σθmax的区段附近，最可能的是

2.1 塑性区域的解

考虑到支承压力 σθmax的增加是的几倍，以及由于坑道附近不可逆变形的发展，在 ri≤r＜rc的区域产生不可恢复变形区域。为分析简单，采用如图2所示的脆性简化模型。图中，τ为剪切应力；γ为剪切应变；τf、τs分别为极限剪切强度与残余强度；γ*为极限剪切应变；μ为剪切模量，这对于阐述机理来说是有好处的，因为复杂的模型往往会掩盖事物的本质。

图2 脆性简化模型Fig.2 Brittle failure model

岩体强度准则采用Tresca准则：

如达到极限剪切应变，应力降为残余强度：

从滑移破坏的观点来看，数值τf是由连续介质变形到“破坏”的过渡点，这时 γ=γ*，滑移面上剪切的发展确定了材料的峰值后的性状，当 γ≥γ*时，岩体被滑移线网格分划成具有一定尺度的块体（或条带），它们之间的相互摩擦决定着残余强度的大小。

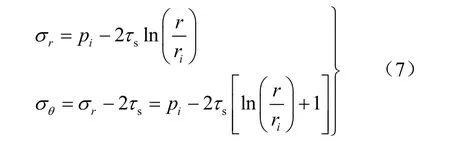
2.2 弹性区域的解

在弹性区域，r≥rc，由胡克定律有力-应变关系为

式中：λ、μ为拉梅系数。

将式（8）代入平衡微分方程式（1）可得

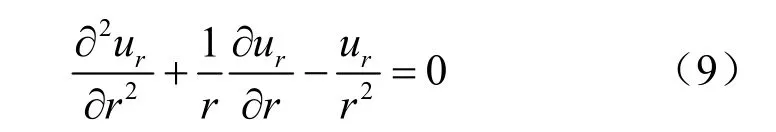
式（9）的解的一般形式可以写成

结合边界条件以及连续性条件：

计算可得弹性区内的应力以及位移：

对于不可恢复区的位移可以按不同的假设计算，设不可恢复区的体积变化是弹性的，则

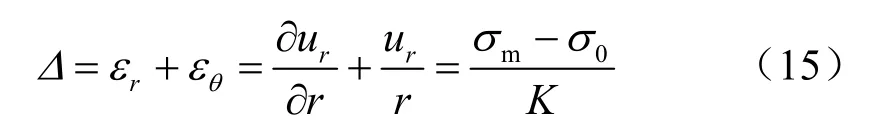
方程式（15）的解为

2.3 算例

令 σc=2τs，计算可以得到

（1）不可恢复区半径

由式（14）可以计算出不可恢复区半径，对其进行无量纲化处理，可以得到如下公式：

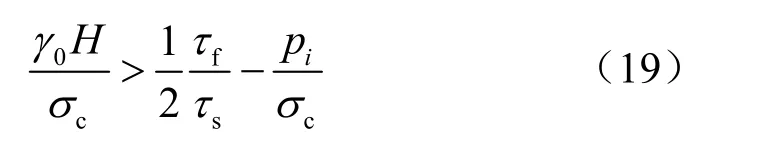
如果不考虑支护强度的影响，要使深地下开挖周围围岩产生不可恢复区的条件为

图 3、4分别为不同支护强度和开挖深度对不可恢复区半径的影响曲线(计算取τf/τs=3/2)，同时由参考公式(4.23)可以知道，支护条件对不可恢复区的半径有着深刻的影响，理论上如果对开挖区及时的施加足够大的支护强度，可以消除不可恢复区的产生，这一临界条件为

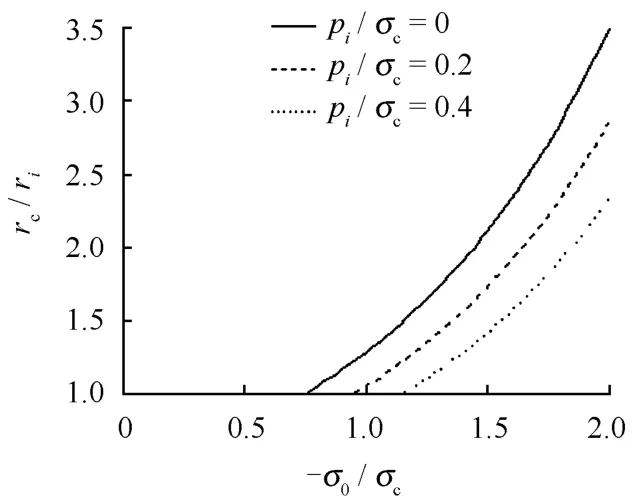
图3 开挖深度对不可恢复半径的影响Fig.3 Effects of excavation depth on radius of irrecoverable deformation area

图4 支护强度对不可恢复半径的影响Fig.4 Effects of support strength on radius of Irrecoverable deformation area

（2）应力位移分布曲线

利用式（7）、（12）、（13）、（16）可以计算得到周围围岩的应力和位移分布曲线。取下列参数进行计算： ri= 3 m，弹性模量 E=5 GPa，泊松比ν=0.25，τs= 15 MPa，τf= 20 MPa，σ0= -45 MPa，pi分别取 pi=0、0.1σ0，可以得到不同支护强度下的应力位移分布曲线，如图5、6所示。

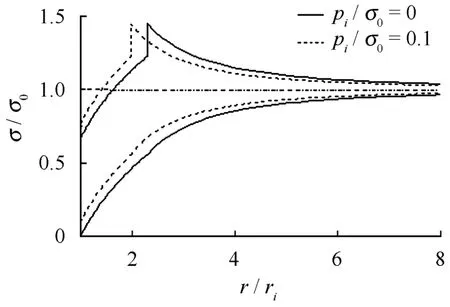
图5 不同支护强度下应力分布曲线Fig.5 Stress distribution curves under different support strengths

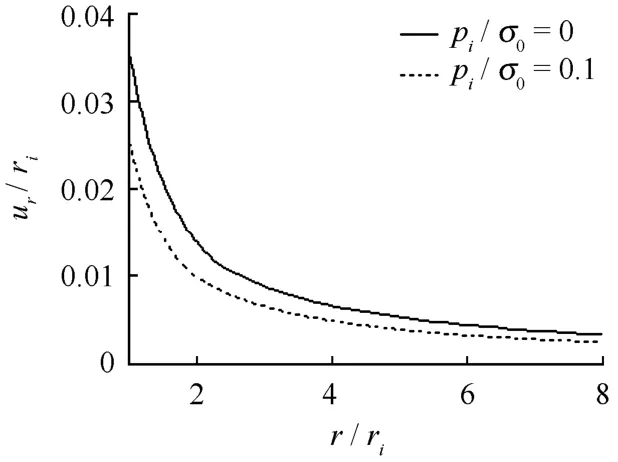
图6 不同支护强度下位移分布曲线Fig.6 Displacement distribution curves under different support strengths

取同样的计算参数，不考虑支护即 pi=0，σ0分别取-σ0=σc=30 MPa，-σ0=1.5σc，-σ0=2σc，则可得不同初始应力状态下的应力位移分布曲线，如图7、8所示。

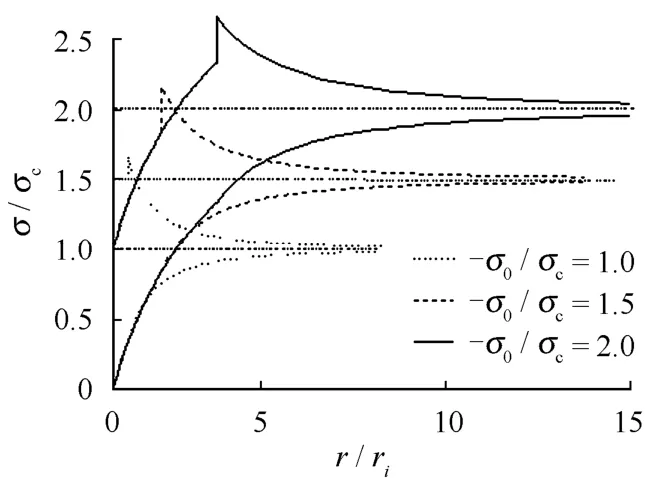
图7 不同初始应力状态下应力分布曲线Fig.7 Displacement curves under different initial geostress states

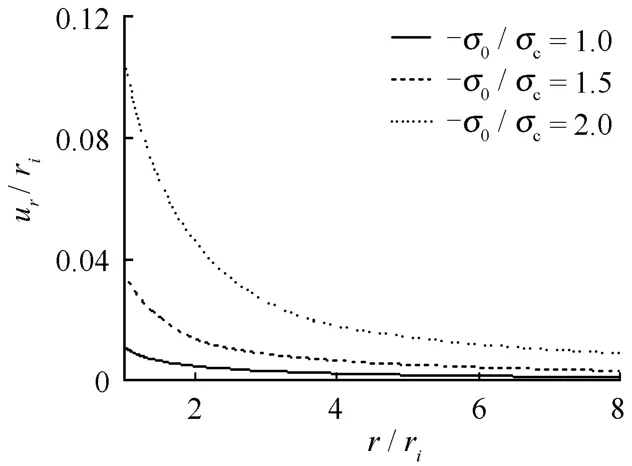
图8 不同初始应力状态下位移分布曲线Fig.8 Displacement distribution curves under different initial geostress states

由图8可见，支护强度对不可恢复区峰值应力值影响不是很大，但是，对于开挖面位移和不可恢复区半径发展影响很大，当支护强度达到一定程度时，对这种影响逐渐减小，实际工程中应该选择合适的支护强度以达到施工成本和支护效果的最大优化比。

（3）开挖面位移

在式（16）中，令r=ir可以得到开挖断面的累计位移，这一位移用ui来表示，则

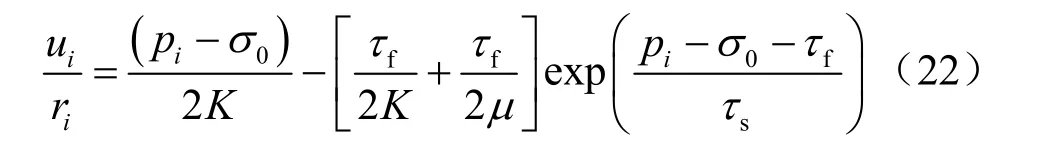
由式（22）可以绘制径向位移与初始应力0σ或者支护压力pi之间的关系曲线，同样利用参数E =5 GPa，ν=0.25，sτ= 15 MPa，fτ= 20 MPa进行计算，可以得到初始地应力以及支护强度对开挖面诱发位移的影响曲线，分别如图9、10所示。

图9 初始地应力对开挖断面累计位移的影响Fig.9 The effects of initial geostress on total displacement

图10 支护强度对开挖断面累计位移的影响Fig.10 The effect of support strength on total displacement

式（22）以及图 10对于实际工程的意义也是显而易见的。利用式（22）可以简单估算控制洞壁位移时所需的支护压力，例如，侧壁的支护压力值为通过式（22）计算所得的-pi，顶板以及底板所需的支护压力值则分别为-pi+γ0（rc-ri）以及-pi-γ0（rc-ri）。

如果在围岩开挖断面监测到的位移超出了按式（22）计算的数值，按可认为在最大应力区附近产生了分层剥离(区域拉伸破碎)。

3 区域拉伸破碎条件计算

根据文献[17]，分层剥离是开挖卸荷围岩体积变化的主要原因，这也可以用来定性解释分区破裂化现象，分层剥离使得围岩开挖断面监测到的位移大大超出按式（22）计算的数值。

取峰值压力(r=rc)附近区域的岩体单元进行研究，由上述计算可知，开挖卸荷的过程中，所取单元的应力状态由最初的静水压力状态逐步转变成与峰值应力相对应的应力状态（图 11中(a)状态转变为(b)状态），如果进一步开挖卸荷，剪切应力τrθ=（σr-σθ）/2将达到极限状态从而进入反向屈服阶段，产生塑性流动。

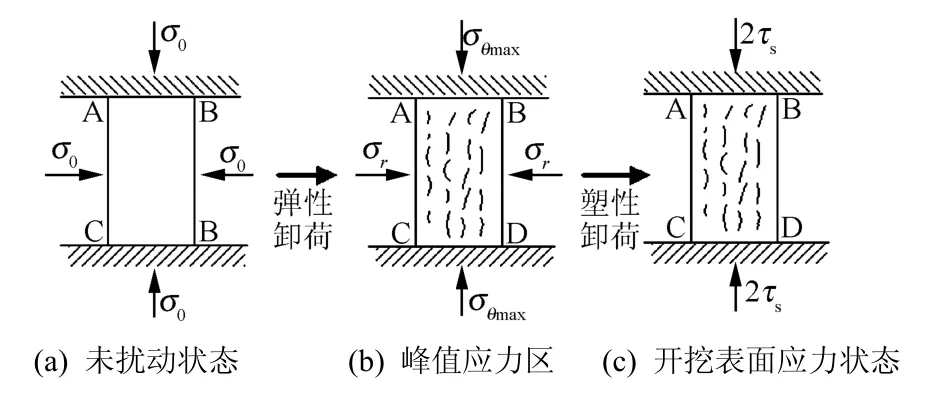
图11 岩体单元应力状态演化示意图Fig.11 Stress state evolution sketch of the rock mass unit

这样所研究单元在大的轴向应力σθ以及小 的径向应力σr压缩作用下，其径向位移εr很容易 达到极限拉伸应变，从而产生“分层剥离”，下面计算产生区域拉伸破碎的条件，为方便计算，引入下列张量符号[18]：

式中：σij为应力张量；δij为特克罗内克尔记号；p为静水力；Sij为偏应力张量。则建议的本构模型可以用下式表示：

式中：εij为应变张量；为塑性应变张量；Kp为考虑到体积膨胀的体积模量。

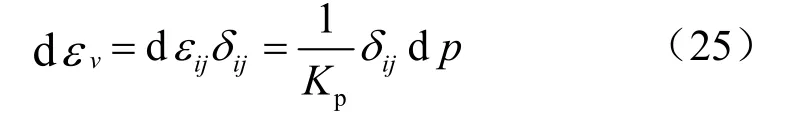
对于深部岩体来说，由于长期处于高地应力作用下，属于密实介质，可以认为其具有体积模量K（K为常数），这是所能得到的岩体的最大体积模量。卸荷时，初始阶段可能是弹性卸荷，而一旦其应力组合满足屈服准则，则可能进入塑性阶段，由于剪切变形的存在引起块体的转动，从而产生密实堆垛的破坏即扩容，从而引起体积模量的减小。卸荷模量Kp是一个变量，应当与岩石的破坏程度有关，目前还没有Kp的详细资料，只能通过实验和插值给出，但明显Kp＜K。

这样可以计算由于开挖造成的指向围岩开挖面的径向应变：由于变形在径向以外的方向的发展受到限制，因此，由于体积膨胀使得材料在径向产生的应变为

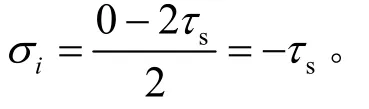
由于弹性变形使得材料在r方向的应变值为

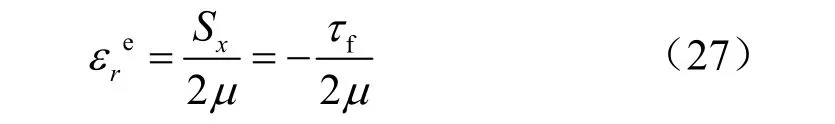
对式（28）进行无量纲化，可以得到

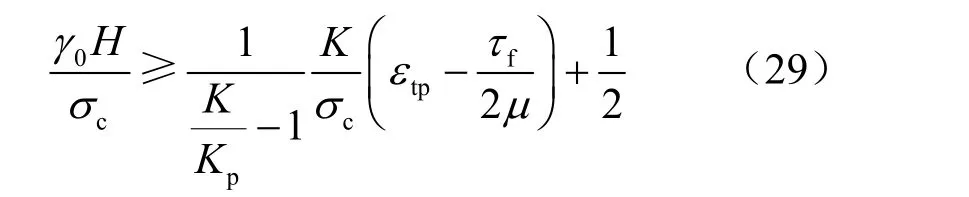
由式（30）可见，产生区域拉伸破碎的埋深条件与岩体的力学性质和破碎尺度密切相关。

4 结 论

（1）滑移剪切变形的发展将围岩划分成具有一定尺度的块体（或条带），它们之间的相互摩擦决定着残余强度的大小。

（2）支护强度对不可恢复区峰值应力值影响不是很大，但对开挖面位移和不可恢复区半径发展影响很大。当支护强度达到一定程度时，对这种影响逐渐减小，实际工程中应该选择合适的支护强度以达到施工成本和支护效果的最大优化比。

（3）开挖卸荷使深部围岩处于各向不均匀压缩作用（大的轴向应力以及小的径向应力）下，从而产生 “分层剥离”（拉伸破碎），分层剥离的存在使得围岩开挖断面监测到的位移大大超出按连续介质理论计算得到的数值。

（4）采用考虑扩容的计算模型可以得到围岩产生区域拉伸破碎的条件，如果不考虑支护强度的影响，要使深地下开挖周围围岩产生不可恢复区的条件为式（20），而产生区域拉伸破碎的条件为式（30）。

[1] GURTUNCA R G, KEYNOTE L.Mining below 3 000 m and challenges for the South African gold mining industry[C]//Proceedings of Mechanics of Jointed and Fractured Rock.Rotterdam: BALKEMA A A, 1998.

[2] YERYOMENKO A A, GAIDIN A P, YERYOMENKO V A, et al.Features of technological block working in a rock-burst hazardous deposite[J].Journal of Mining Science, 2000, 36(6): 592－594.

[3] SHEMYAKIN E I, FISENKO G L, KURLENYA M V.Zonal disintegration of around underground workings,PartⅠ.Date of in situ observations[J].Journal of Mining Science, 1986, 22(3): 157－168.

[4] 钱七虎.深部岩体工程响应的特征科学现象及“深部”的界定[J].东华理工学院学报(自然科学版).2004,27(1): 1－5.QIAN Qi-hu.The characteristic scientific phenomena of engineering response to deep rock mass and the implication of deepness[J].Journal of East China Institute of Technology (Natural Science), 2004, 27(1):1－5.

[5] FENG Xia-ting.New rock mechanics development in China[C]//12th ISRM International Congress on Rock Mechanics.Beijing: [s.n.], 2011: 71－79.

[6] 何满潮, 谢和平, 彭苏萍, 等.深部开采岩体力学研究[J].岩石力学与工程学报, 2005, 24(16): 2803－2813.HE Man-chao, XIE He-ping, PENG Su-ping, et al.Study on rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005, 24(16): 2803－2813.

[7] HUDSON J A.The next 50 years of the ISRM and anticipated future progress in rock mechanics[C]//12th ISRM International Congress on Rock Mechanics.Beijing: [s.n.], 2011: 47－55.

[8] 钱七虎.岩土工程的第四次浪潮[J].地下空间, 1999,19(4): 267－272.QIAN Qi-hu.The fourth wave of geotechnology[J].Underground Space, 1999, 19(4): 267－272.

[9] 王明洋, 周泽平, 钱七虎.深部岩体的构造和变形与破坏问题[J].岩石力学与工程学报, 2006, 25(3): 448－455.WANG Ming-yang, ZHOU Ze-ping, QIAN Qi-hu.Tectonic, deformation and failure problems of deep rock mass[J].Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 448－455.

[10] 顾金才, 顾雷雨, 陈安敏.深部开挖洞室围岩分层断裂破坏机制模型试验研究[J].岩石力学与工程学报, 2008,27(3): 433－438.GU Jin-cai, GU Lei-yu, CHEN An-min.Model test study on mechanism of layered fracture within surrounding rock of tunnels in deep stratum[J].Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 433－438.

[11] 谢和平, 鞠杨, 黎立云.基于能量耗散与释放原理的岩石强度与整体破坏准则[J].岩石力学与工程学报, 2005,24(17): 3003－3010.XIE He-ping, JU Yang, LI Li-yun.Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3003－3010.

[12] 周小平, 钱七虎, 张伯虎, 等.深埋球形洞室围岩分区破裂化机理[J].工程力学, 2010, 27(1): 69－75.ZHOU Xiao-ping, QIAN Qi-hu, ZHANG Bo-hu, et al.The mechanism of the zonal disintegration phenomenon around deep spherical tunnels[J].Engineering Mechanics, 2010, 27(1): 69－75.

[13] 周小平, 钱七虎.深埋巷道分区破裂化机制[J].岩石力学与工程学报, 2007, 26(5): 877－885.ZHOU Xiao-ping, QIAN Qi-hu.Zonal fracturing mechanism in deep tunnel[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 877－885.

[14] QI Cheng-zhi, WANG Ming-yang, QIAN Qi-hu.Evolution of the deformation and fracturing in rock masses near deep-level tunnels[J].Journal of Mining Science, 2009, 45(2): 112－119.

[15] 吴文平, 冯夏庭, 张传庆, 等.深埋硬岩隧洞围岩的破坏模式分类与调控策略[J].岩石力学与工程学报, 2011,30(9): 1782－1802.WU Wen-ping, FENG Xia-ting, ZHANG Chuan-qing,et al.Classification of failure modes and controlling measures for surrounding rock of deep tunnel in hard rock[J].Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1782－1802.

[16] JACGER J C, COOK N G.Fundamentals of rock mechanics[M].London: Chapman and Hall, 1979.

[17] 钱岳红, 王德荣, 李杰, 等.掌子面前支撑压力带岩层变形破坏机制研究[J].岩土力学, 2011, 32(10), 3058－3064 QIAN Yue-hong, WANG De-rong, LI Jie, et al.Study of mechanism of rock mass deformation and failure ahead of working face on supporting zone[J].Rock and Soil Mechanics, 2011, 32(10): 3058－3064.

[18] 郑颖人, 沈珠江, 龚晓南.岩土塑性力学原理[M].北京: 中国建筑工业出版社, 2002.