多级边坡平台宽度对边坡地震动力响应及破坏机制的影响

言志信，郭 斌，贺 香，江 平

(1.兰州大学 土木工程与力学学院，兰州 730000；2.兰州大学 西部灾害与环境力学教育部重点实验室，兰州 730000)

1 前 言

我国是一个多山的地震多发国家，5·12四川汶川地震诱发大量的滑坡、崩塌等灾害，并导致了一系列次生地质灾害的发生[1－2]，给经济造成巨大损失的同时，给社会带来极为严重的灾难。因此，边坡在地震动力作用下的破坏研究显得尤为重要。

近年来，地震作用下边坡动力响应规律的研究取得了一些成果，薄景山等[3]对无限域中土质边坡在动力作用下的位移场和应力场进行了研究，并提出边坡动力稳定性的定量评价方法。祁生文等[4－6]通过数值计算分析了边坡动力响应规律，探究地震作用下边坡稳定性的影响因素。张林等[7]考虑爆破地震的时程效应，借助拟静力法提出了爆破地震作用下边坡动力稳定性系数的计算方法。郑颖人等[8]、徐光兴等[9－10]通过数值模拟和振动台试验，研究了边坡动力响应规律，对地震作用下边坡的变形破坏机制进行了探讨。谷天峰等[11]在不排水三轴试验的基础上，建立某一黄土边坡的动力分析模型，分析了机车振动荷载作用下边坡的变形规律，得到了一些有益的结论。龚成明等[12]对黄土边坡动力响应规律进行了试验研究，揭示了黄土边坡在强夯激励下的动力响应规律，但鲜见地震作用下多级边坡平台宽度对边坡动力响应特性及地震动力失稳机制研究的报道。

本文分析地震作用下多级边坡平台宽度对边坡稳定性的影响，研究了多级边坡动力响应特性，包括水平加速度PGA放大系数及其频谱分析，分析了典型工程边坡地震动力作用后其塑性区状态及其分布范围、持时对塑性区及位移影响规律，探讨了边坡地震动力失稳机制。由于FLAC3D有限差分软件具有分析非线性动力学问题等优点，被广泛应用于岩土工程开挖、边坡稳定性及地震动力响应分析等诸多领域。利用FLAC3D有限差分法建立了一个三级土边坡模型，利用FLAC3D自带的动力分析模块进行数值计算分析，对不同平台宽度在地震作用下边坡的动力响应特性和地震动力失稳机制进行了探讨。

2 边坡动力分析模型及输入地震波

2.1 模型尺寸及边界条件

为了探讨平台宽度对分级边坡动力响应特性和地震动力失稳机制的影响，选择4种不同平台宽度的模型进行数值计算，模型坡脚至左侧边界距离为40 m，坡顶至右侧边界距离为70 m，边坡高30 m，模型底部至顶部为2倍坡高即 60 m，模型宽度取20 m，坡比为 1: 0.75。边坡材料弹性模量为 102 MPa，密度为1 610 kg/m3，泊松比为0.3，黏聚力为3.8 kPa。计算模型即三维地质模型如图1所示。

为了保证地震波在模型边坡中的精确传播[13]，最大网格尺寸设为 2 m。在模型边坡两侧边界施加位移约束条件。同时，在动力分析时施加自由场边界条件；模型底部施加位移约束条件，同时在动力计算时施加黏滞边界条件。由于在模型底部施加了黏滞边界条件，故在动力计算时须将模型底部输入的加速度时程转化为应力时程，并施加到黏滞边界条件上。模拟计算中的阻尼采用局部阻尼，阻尼系数为0.156。本文首先施加重力，计算自重作用下的应力应变场，然后，清除自重作用形成的位移场和速度场，施加图 2 所示的地震动速度时程，进行地震作用下的边坡动力响应分析，并在坡面垂直方向每隔3.5 m设置 1 个监测点，另外，每级坡脚和坡顶也是监测点，从坡脚到坡顶总共设12个监测点。本文计算采用弹塑性本构模型和摩尔-库仑破坏准则[8－9]。

图1 计算模型及动力边界条件Fig.1 Calculation model and dynamic boundary

图2 地震动速度时程曲线Fig.2 Input seismic velocity time history

2.2 输入波形

为模拟地震动力作用下边坡的动力响应特性，在边坡模型底部输入水平地震波，本文地震动加载试验输入的地震波为kobe波，所施加的加速度幅值为0.225g，持时25 s，主频为1～4 Hz，加速度时程曲线见图 2 ，输入的地震波根据需要进行了过 滤和基线调整。本文在边坡底部设置了监测点，用来指示动力条件施加是否合适，结果表明底部监测点的加速度时程与输入的加速度时程曲线吻合较好，说明本文数值计算所输入的地震波是合适的。

3 动力计算结果分析

首先计算了自重应力条件下典型工程边坡的安全系数，见表 1。由表可以看出，施加平台显著地提高了边坡的静力安全系数。为研究边坡平台宽度B对土质边坡地震动力反应的影响，本文对于高30 m的3级土质边坡（见图1），分别设置了平台宽度为2、3、4、5 m四种工况进行了数值计算。

表1 数值计算工况Table 1 Condition of numerical calculation

3.1 加速度响应规律

边坡加速度响应规律可以通过加速度时程傅氏谱形状PGA放大系数、加速度时程傅氏谱、加速度时程等三方面来考察，本文通过前两方面来探究加速度响应规律。图3为不同平台宽度下坡面监测点PGA放大系数图。结果表明，随着平台宽度B的增加，PGA放大系数逐渐减小，即水平向的地震动加速度有不同程度的减小，设置平台有利于边坡抗震。

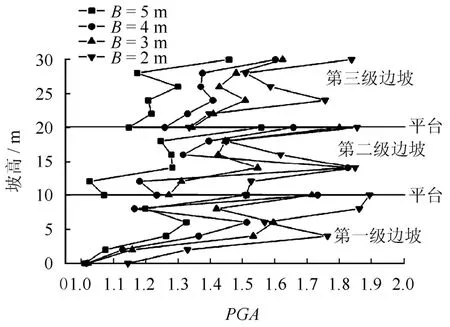
图3 不同平台宽度下坡面PGA放大系数Fig.3 Variation of coefficients of amplification for PGA along slope surface with different platform widths

由图3不同工况下的边坡PGA放大系数随坡高变化曲线图可以看出，PGA放大系数随坡高变化趋势基本相同，每一级边坡内 PGA放大系数都随坡高增加而增大，在每级边坡的坡顶均达到最大值；PGA放大系数在平台处均出现一个律动，即第一级边坡坡顶和第二级边坡坡底出现律动，第二级边坡坡顶和第三级边坡坡底两个律动。每个律动 PGA放大系数均呈减小的趋势，即第一级边坡坡顶PGA放大系数明显大于第二级边坡坡底PGA放大系数，亦即边坡第一级平台外侧坡面处的 PGA放大系数明显大于平台内侧 PGA放大系数，即第二级边坡坡底处PGA放大系数。同理，边坡第二级平台外侧坡面处的 PGA放大系数明显大于平台内侧即第三级 边坡坡底处PGA放大系数。平台部位出现律动，说明边坡坡顶动力响应较坡脚显著，是比较危险的部位，动力作用下边坡稳定性降低较大。出现律动主要是坡顶对地震动力响应比较敏感，加之平台外侧具有坡面和坡顶两个临空面，对地震波具有反射、折射作用，从而引起反射波和折射波的叠加，致使平台部位出现律动现象；随着平台宽度加宽，位于平台内侧的监测点 PGA放大系数则越小，这一现象是由于岩土体自身对地震波的阻尼衰减作用，也是因为没有坡面和坡顶等自由临空面对地震波产生折射反射及相互叠加耦合作用的缘故[15]。

图4 水平加速度傅氏谱Fig.4 Furier spectra of horizontal acceleration

从第一级边坡坡顶和第二级边坡坡脚水平加速度频谱分析也可以得出，边坡第一级平台外侧动力响应比第二级边坡坡脚，即边坡第一级平台内侧显著，与 PGA放大系数在平台部位出现律动是一致的，可以相互印证结论的正确性。

3.2 平台宽度对塑性区范围、剪应变及位移的影响

从图 5 可以看出，随着平台宽度的增加，地震动力作用下边坡塑性区范围不同程度地缩小，坡顶拉张塑性区范围大大缩小；坡体拉张剪切塑性区趋向坡面，塑性区范围不同程度的缩小。当 B=2 m或 B=3 m 时，近坡面的浅层拉张-剪切塑性区和坡顶拉张塑性区已经贯通，故在地震动力作用下比较危险，应加强坡面下浅层及坡脚部位的加固处理；当 B=4 m 或 B=5 m 时，坡面下拉张-剪切塑性区与坡顶拉张塑性区未贯通，坡脚处是地震动力作用下最薄弱的部位，这与地震动力使不同部位边坡岩土体的扰动程度不一样，从而引起应力调整和重分布有关，如若在平坦场地条件下应力场分布均匀，而具有临空面的边坡在动力作用下，使坡面及坡体一定部位应力场，尤其是剪应力场调整十分明显，产生剪切屈服区，如果坡面浅表层剪切塑性区与坡顶拉张塑性区贯通，并贯穿坡体，边坡将失稳破坏。另外剪应力在坡脚的集中程度也较大，地震动力作用下边坡坡脚更易于破坏，故边坡防护时应重点防护坡脚。计算结果与实际地震边坡破坏过程及其震害模式相仿[14]，可以证明数值计算方法适用于边坡动力计算。

图5 地震作用后不同平台宽度下边坡塑性区Fig.5 Plastic zone of slope with different platform widths under earthquake

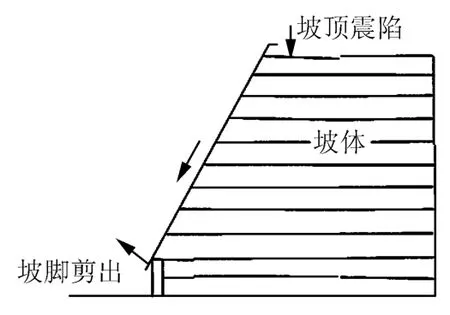
图6 地震边坡滑裂震害模式[14]Fig.6 Seismic settlement model of slope[14]

从典型工程边坡动力作用下剪应变增量云图可以看出，三级土质边坡首先从一级边坡坡脚处产生塑性剪切变形，并逐渐向坡体内、坡顶扩展，如图7所示，本算例边坡地震动力作用下剪切变形塑性区和潜在滑裂面不是很深，潜在滑裂面深度大概为5～10 m范围内。故应加强坡脚的防护与监测。

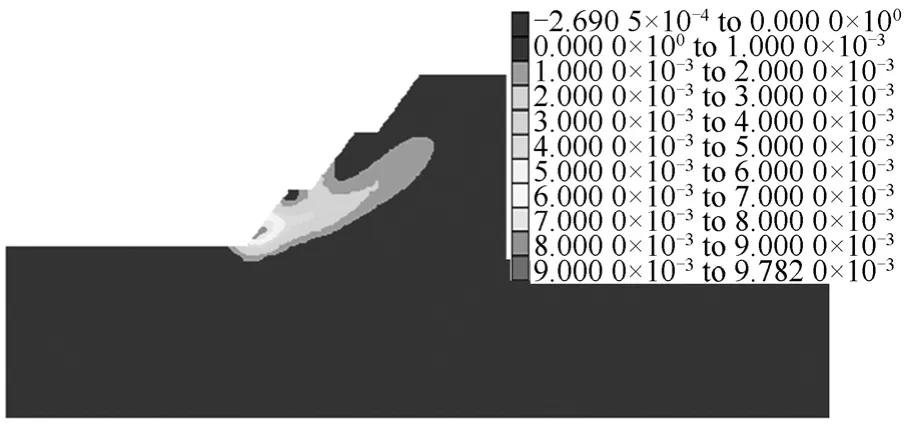
图7 边坡动力作用下剪应变增量云图(B=3 m)Fig.7 Shear strain increment nephogram of slope under dynamic failure(B=3 m)

边坡剪应变增量随平台宽度变化情况见表2，表明剪应变增量随平台宽度的增加而显著减小，剪应变增量从平台宽度B=2 m的1.68×10－2，减小到B=5 m 时的8.16×10－3，减小了1个数量级，表明设置平台宽度有利于提高边坡地震动力稳定性，并且平台宽度越大剪应变增量越小，故在高烈度区进行边坡支护设计时，可以采用设置不同宽度的平台来提高边坡的地震稳定性。

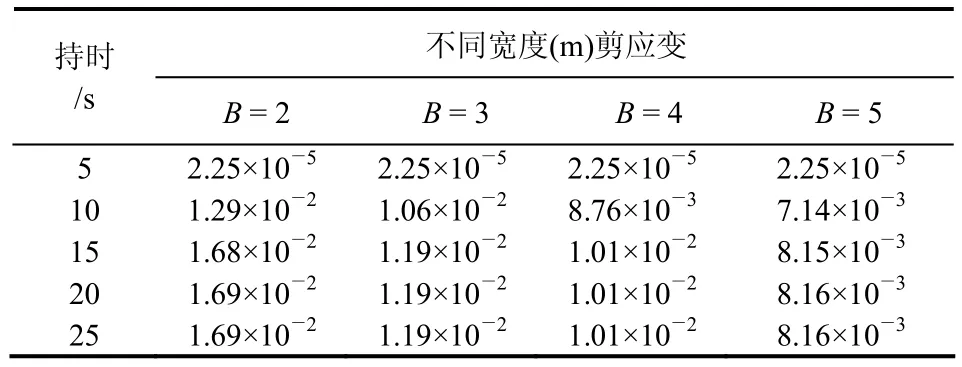
表2 剪应变增量最大值与平台宽度、地震波持时关系Table 2 Relation between maximum shear strain increment and duration or platform width

表3为不同平台宽度下监测点的竖直向和水平向的位移最大值，表明地震动力作用下，随着平台宽度的增加，多级边坡竖直向和水平向位移均有不同程度的减小，竖向位移从B=2时的9.5 cm减小到B=5时的4.6 cm，减小了50%左右；水平位移从B =2时的12.8 cm减小到B=5时的9.1 cm，减小了30%左右，竖向变化大是由于岩土体具有震陷性所致。

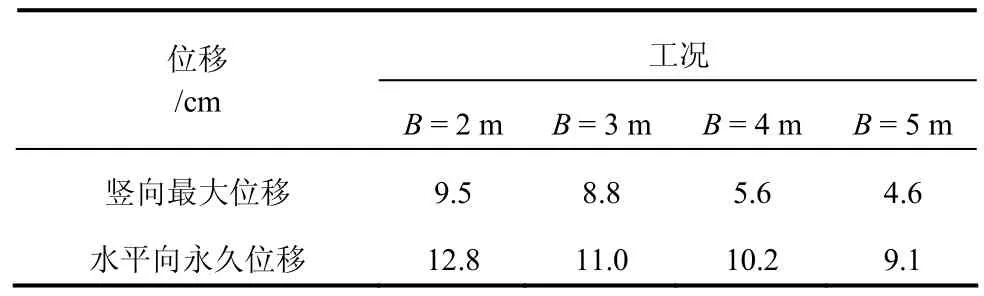
表3 不同工况下监测点竖直和水平向最大位移Table 3 Vertical and horizontal displacements of monitoring points under different conditions

3.3 持时对边坡塑性区范围、剪应变及位移的影响

从图 8 可以看出，持时对边坡的塑性区影响很大，随着地震作用持时的增加，边坡塑性区开始从坡脚向边坡坡体内部和坡顶扩展，刚开始即当t =5 s时，边坡坡脚处有小部分的拉张剪切塑性区，见图8(a)；当t=15 s时，坡顶出现拉张塑性区，拉张剪切塑性区扩展到坡面及其浅表层部位，坡体内局部发生剪切塑性区，见图8(b)；当t=25 s 时，坡顶拉张塑性区向坡体深部发展，近坡面拉张剪切塑性区向坡体内深部发展，见图8(c)。故可将地震作用下均质土坡塑性区可以分为 4 个区域：Ⅰ稳定区、Ⅱ拉 张塑性区、Ⅲ拉张-剪切塑性区和Ⅳ剪切塑性区。若拉张，拉张-剪切、剪切塑性区贯通，则边坡有失稳的可能。对比不同平台宽度下塑性区状态及其分布范围，表明平台宽度越大，塑性区范围明显减小。

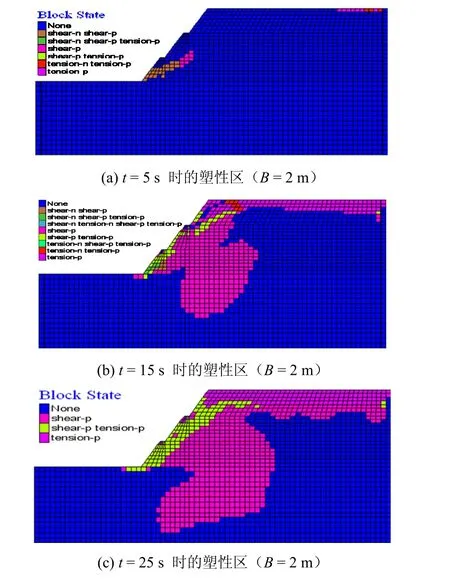
图8 持时对边坡塑性区的影响Fig.8 Influence of earthquake duration on plastic zone of slope

边坡剪应变增量随持时变化情况见表2，剪应变增量最大值随持时的增加而增加。本文算例剪应变随地震动持时的增加而增加到一定值后趋于稳定，表明该边坡是并没有失稳，故在一定程度上可用剪应变增量是否收敛作为判断边坡失稳破坏的判据。

从图9、10（图9、10中1-12是从坡脚到坡顶的监测点，包括每一级边坡的坡脚、坡顶、每一级坡脚到坡顶之间平均内插 2 个监测点，总共12个监测点）坡面监测点的位移时程曲线可以看出，地震作用下边坡坡面上从坡脚至坡顶监测点的竖向位移逐渐增大，而各级平台的水平位移出现波动；随着地震动持时增加，边坡产生了一定的塑性位移即永久变形，坡顶竖向最大永久位移为9.5 cm，水平向的最大永久位移为12.8 cm，整体而言，竖向位移大于水平向位移，即地震动作用下边坡坡脚有发生剪出破坏趋势或发生剪出破坏，坡顶则有发生震陷破坏的可能或发生震陷破坏，与文献[14]调查结果一致。边坡的塑性位移是累积形成的永久位移，大体上位移最大值与地震动峰值同时出现，一段时间后相对位移趋于某一恒定值（图10）或收敛（图9），表明边坡并没有发生失稳破坏。由图9、10还可以看出，各级边坡坡脚竖向位移方向向上，说明坡脚发生了剪出变形，具有发生剪出破坏的趋势。

图9 坡面监测点水平位移时程曲线（B=2 m）Fig.9 Horizontal displacement time histories of monitoring points in slope surface (B=2 m)

图10 坡面监测点竖向位移时程曲线（B=2 m）Fig.10 Vertical displacement time histories of monitoring points in slope surface (B=2 m)

3.5 边坡动力失稳机制探讨

地震对边坡稳定性的影响表现在：地震波在边坡岩土体内传播和作用过程中，边坡坡体内产生的横波和纵波使边坡岩土体不同部分发生相互作用，产生拉张或剪切变形甚至导致边坡岩土体破坏，同时地震波在传播过程中遇到界面时将发生反射、折射，不同地震波还将叠加协同作用，致使岩土体产生拉张变形和剪切变形。

边坡对地震动的反应强度存在两个重要现象：由于临空面的存在，造成入射波与反射波叠加所产生的放大效应和土体本身阻尼对入射波吸收所造成的衰减效应。另外，由弹性波散射理论可知，坡底垂直入射的SV波传播到坡顶时将产生波场分裂现象，分解为同类型的SV波和新类型的反射P波（转换波），各种类型的波相互叠加形成复杂的地震波场，使得峰值加速度、峰值速度在靠近坡顶段急剧增大。概括地说，边坡岩土体在地震动作用下的应力状态是由地震作用形成的地震动应力和边坡岩土体自重应力形成的静应力的叠加，边坡岩土体的变形破坏归根结底是由于地震动力作用所产生的动应力改变了原有的初始平衡应力场，动应力和初始静应力相互耦合作用，从而导致了边坡岩土体的变形破坏。

4 结 论

（1）多级土质边坡的平台宽度加大，坡面动力响应将减弱，边坡剪应变减小，水平加速度减小，静力稳定安全系数增大。第一级边坡坡顶动力响应比第二级边坡坡脚显著，设置平台有利于土质边坡的抗震稳定性。

（2）地震作用下边坡坡顶一定区域内发生拉张变形或破坏，坡面及浅表层坡体发生拉张-剪切变形或破坏，坡体内的破坏大多为剪切变形。地震作用下边坡按其塑性变形形式可分为Ⅰ稳定区、Ⅱ拉张塑性区、Ⅲ拉张-剪切塑性区和Ⅳ剪切塑性区4个区域。随着平台宽度的增加，地震动力作用下，边坡岩土体各塑性变形区范围显著减小。

（3）随着平台宽度的增加，地震结束后产生的永久位移，包括竖向和水平向的位移均有所减小。

[1] 郑颖人, 叶海林, 黄润秋, 等.边坡地震稳定性分析探讨[J].地震工程与工程振动, 2010, 30(2): 173－180.ZHENG Ying-ren, YE Hai-lin, HUANG Run-qiu, et al.Study on the seismic stability analysis of a slope[J].Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(2): 173－180.

[2] 殷跃平.汶川八级地震地质灾害研究[J].工程地质学报, 2008, 16(4): 433－444.YIN Yue-ping.Researches on the geo-hazards triggered by Wenchuan earthquake, Sichuan[J].Journal of Engineering Geology, 2008, 16(4): 433－444.

[3] 薄景山, 徐国栋, 景立平.土边坡地震反应及其动力稳定性分析[J].地震工程与工程振动, 2001, 21(2): 116－120.BO Jing-shan, XU Guo-dong, JING Li-ping.Seismic response and dynamic stability analysis of soil slopes[J].Earthquake Engineering and Engineering Vibration,2001, 21(2): 116－120.

[4] 祁生文.单面边坡的两种动力反应形式及其临界高度[J].地球物理学报, 2006, 49(2): 518－523.QI Sheng-wen.Two patterns of dynamic responses of single free surface slopes and their threshold height[J].Chinese Journal of Geophysics, 2006, 49(2): 518－523

[5] 祁生文, 伍法权.边坡动力响应规律研究[J].中国科学E 辑, 2003, 33(增刊): 28－32.QI Sheng-wen, WU Fa-quan.Study on the regularity of dynamic response for slope [J].Science in China Series E, 2003, 33(Supp.): 28－40.

[6] 祁生文, 伍法权, 刘春玲, 等.地震边坡稳定性的工程地质分析[J].岩石力学与工程学报.2004, 23(16): 2792－2797.QI Sheng-wen, WU Fa-quan, LIU Chun-ling, et al.Engineering geology analysis on stability of slope under earthquake[J].Chinese Journal of Rock Mechanics and Engineering, 2004, 23(16): 2792－2797.

[7] 张林, 林从谋.爆破震动对土质边坡动力稳定性影响研究[J].岩土力学, 2005, 26(9): 1499－1501.ZHANG Lin, LIN Cong-mou.Study about soil slope dynamic stability due to blasting vibration[J].Rock and Soil Mechanics, 2005, 26(9): 1499－1501.

[8] 郑颖人, 叶海林, 黄润秋.地震边坡破坏机制及其破裂面的分析探讨[J].岩石力学与工程学报.2009, 28(8):1715－1720.ZHENG Ying-ren, YE Hai-lin, HUANG Run-qiu.Analysis and discussion of failure mechanism and fracture surface of slope under earthquake[J].Chinese Journal of Rock Mechanics and Engineering, 2009,28(8): 1714－1723.

[9] 徐光兴, 姚令侃, 李朝红, 等.边坡地震动力响应规律及地震动参数影响研究[J].岩土工程学报.2008, 30(6):918－923.XU Guang-xing, YAO Ling-kan, LI Zhao-hong, et al.Dynamic response of slopes under earthquakes and influence of ground motion parameters[J].Chinese Journal of Geotechnical Engineering, 2008, 30(6): 918－923.

[10] 徐光兴, 姚令侃, 高召宁, 等.边坡动力特性与动力响应的大型振动台模型试验研究[J].岩石力学与工程学报.2008, 27(3): 624－632.XU Guang-xing, YAO Ling-kan, GAO Zhao-ning, et al.Large-scale shaking table model test on the dynamic characteristics and seismic responses of slope[J].Chinese Journal of Rock Mechanics and Engineering, 2008,27(3): 624－632.

[11] 谷天峰, 王家鼎, 任权, 等.循环荷载作用下黄土边坡变形研究[J].岩石力学与工程学报, 2009, 28(增刊1):3156－3162.GU Tian-feng, WANG Jia-ding, REN Quan, et al.Study on derormation of loess slope under cyclic load[J].Chinese Journal of Rock Mechanics and Engineering.2009, 28 (Supp.1): 3156－3162.

[12] 龚成明, 程谦恭, 刘争平.强夯激励下黄土边坡动力响应模型试验研究[J].岩土力学, 2011, 32(7): 2001－2006.GONG Cheng-ming, CHENG Qian-gong, LIU Zheng-ping.Model test study of dynamic responses of loess slope by dynamic compaction[J].Rock and Soil Mechanics, 2011, 32(7): 2001－2006.

[13] 陈育民, 徐鼎平.FLAC/FLAC3D基础与工程实例[J].北京: 中国水利水电出版社, 2008.

[14] 王建, 姚令侃, 蒋良潍.地震作用下土体变形破坏模式与机理[J].西南交通大学学报, 2012, 45(2): 196－202.WANG Jian, YAO Ling-kan, JIANG Liang-wei.Seismic deformation and falure modes and mechanism of soilMass[J].Journal of Southwest Jiaotong University,2012, 45(2): 196－202.

[15] YAN Z X, CAI H C, WANG Q M, et al.Finite difference numerical simulation of guided wave propagation in the full grouted rock bolt[J].Science China Technological Sciences, 2011, 54: 1－8.