考虑基坑开挖宽度的杆系有限元算法及试验研究

王洪新，孙玉永

（1.上海城建市政工程（集团）有限公司，上海 200065；2.铜陵学院 土木建筑系，安徽 铜陵 244000）

1 引 言

杆系有限元方法在基坑设计中处于重要的地位，是基坑设计中被广泛应用的计算工具。杆系有限元把基坑简化成围护结构、结构承受的荷载、支撑单元及被动区土体弹簧。这些假设造成该方法的诸多缺点，比如：围护上承受的荷载不明确，被动区土体弹簧刚度难以准确确定等。但由于各地区的设计院长期采用杆系有限元方法计算基坑变形，结合现场的大量反馈数据，可以形成经验性的被动区土体弹簧刚度。目前，以杆系有限元为主要计算手段的启明星和理正计算软件已经成为国内基坑设计的主要工具，充分反映了杆系有限元方法在基坑设计中的强大生命力。

杆系有限元的支撑刚度采用 k=2 EA/l（E为支撑弹性模量，A为支撑横截面积，l为支撑受压计算长度）计算，在一定意义上可以考虑基坑宽度对支撑刚度的影响。但现场经验表明：基坑存在明显的空间效应，狭窄基坑不但具有良好的稳定性[1]，而且变形也相对较小，而同样挖深的宽基坑则变形更大，并且伴有明显的“踢脚”现象。同样是一级保护基坑，采用相同支撑刚度设计时，窄基坑的实际变形能够满足规范要求，而宽基坑的实际变形却极有可能超出限制。目前采用的杆系有限元计算方法是不能反映基坑的这种二维空间效应的。超宽基坑围结构变形一般比同样挖深的窄基坑大很多，如果采用常规杆系有限元方法计算，除非把支撑和被动区土体刚度取得比经验值小得多，否则往往不能准确计算出超宽基坑的变形值。

目前，国内基坑施工面积最大已经达3×105m2，基坑施工面积和宽度越来越大；而一些地铁车站风井、出入口及顶管工作井基坑宽度很窄，其数量占基坑工程很大比例。这些都迫切需要解决基坑宽度对变形的影响问题。

张雷等[2]通过二维平面有限元研究发现，相同条件下，基坑越宽对周围环境的影响越大。曾庆义等[3]假设：基坑开挖时，如同在地表施加了一个负载。他采用弗拉曼解答推导了开挖引起的二次应力场，为采用解析方法考虑基坑宽度影响提供了一个很好的思路。胡玉银[4]针对曾庆义的文章进行了讨论，并对基坑开挖的二次应力场给出了建议。应宏伟等[5]通过在基坑开挖面施加反向自重应力模拟基坑的开挖卸荷，考虑不同卸荷比对土体水平抗力系数影响，对传统的杆系有限元法进行改进。他的研究表明：当宽深比越大，桩底端位移即“踢脚”变形越明显。本文采用另一种思路，不是调整被动区土体刚度，而只调整围护上的土压力荷载来反映基坑宽度对变形的影响。这种处理方法同样能够反映基坑二维尺寸效应，而且操作起来更加简单。

2 围护结构上土压力计算

2.1 传统的基坑杆系有限元方法土压力取值

采用杆系有限元进行基坑计算时，一般采用增量法，相应的土压力取值也是增量荷载。围护结构上土压力较为复杂，被动区土体弹簧刚度与土压力荷载取值模式共同作用影响基坑变形的计算结果。如果同时调整围护上土压力荷载和被动区土体弹簧刚度，可能得到相近的计算结果。因此，不同地区提出了不同的土压力荷载模式。目前，国内基坑设计时最常用的是矩形分布荷载，每次开挖时围护结构上的荷载取值如图 1所示，图中γhi为卸载土层的自重应力，其中，γ为土体重度，hi为每次开挖土体的深度，ξ为侧压力系数。实际上，坑底以下部分的矩形土压力荷载是基坑开挖无限宽时的荷载取值。如果基坑宽度很小，坑底以下荷载形式会有很大差异，这一点会在下文详细论述。不同地区的矩形分布荷载取值也存在较大差异，比如日本《建筑基础结构设计规范》规定：地下水位以上部分，按土体单位重度计算竖直向压力，乘以侧压力系数0.5；地下水位以下部分，按土体单位浮重度计算竖向压力，乘以侧压力系数0.5[6]，下文将说明这种计算模式的合理性。

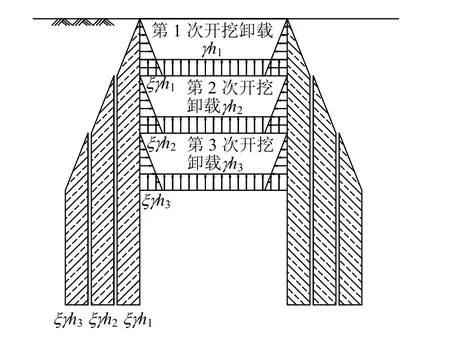
图1 基坑增量法计算的分步开挖荷载计算模型Fig.1 Calculation model of stepwise excavation load through incremental method

2.2 考虑基坑宽度的围护结构上土压力取值

文献[3]给出了一个考虑基坑开挖宽度影响的方法，计算时在地表施加与开挖荷载相等、方向相反的负载来模拟开挖，有一定意义。但由于没有把负载施加于真正的开挖面，故与实际开挖工况差异较大。实际上，完全采用解析解计算基坑开挖问题较为困难，但如果适当简化还是可以推导出与工程实际相近的结果的。

计算每次开挖所产生的增量荷载时，取图2所示的开挖卸载模式计算，把竖向开挖荷载作用于开挖面处，并且在侧面施加如图所示的三角形荷载。由于荷载应力作用于半空间以下，采用Melan解可以推导出开挖卸载引起的附加应力。

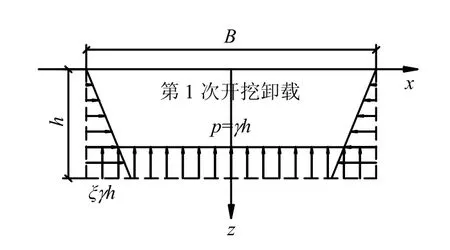
图2 基坑开挖卸载应力计算图Fig.2 Unloading stress calculation model induced by excavation

首先计算由于坑底竖向卸载引起的水平向附加应力σXp。此时的Melan解如下[7]：

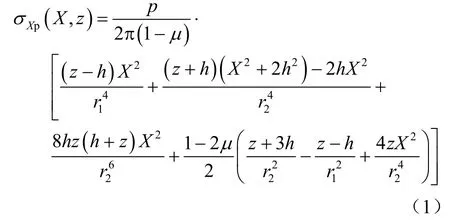
式中：μ为泊松比，由于土体为饱和软弱黏土层，体积变形较小，因此取为0.45；X、z为Melan解坐标系下计算点的坐标值；；h为开挖面深度。

取如图2所示的坐标系，开挖相当于在开挖面施加一个长为B的负载-p=-γhi，hi为分层开挖时第i次开挖的深度，则由于竖向卸载在围护上产生的侧向压力 px(z)可采用下式计算：

式中：B为基坑宽度；x为侧向压力计算点的横坐标，在围护处x=-B/2。

积分后，整理可得竖向卸载引起的围护墙体上侧向压力荷载为

根据Melan解，由于对称性，围护结构处水平向卸荷在开挖面以下部分围护上不引起侧向荷载，这一点在分析基坑开挖时有一定的近似性，实际开挖时，这个附加荷载也很小。所以，可以直接采用式（3）计算开挖卸载在坑底下部分围护上引起的荷载。由于围护结构在开挖面以下部分承受的荷载是坑内开挖卸载后围护结构两侧土压力差引起的，以往采用的荷载模式实际上是开挖无限宽基坑时围护两侧的压力差。对于狭窄基坑，传统算法在坑底以下部分围护上的土压力计算值过大。式（3）是基于弹性力学的解析解推导出的，能够考虑开挖宽度的影响，尽管是近似解，但有一定的科学性。

图3 基坑围护上土压力计算模型Fig.3 Calculation model for earth pressure on enclosure structures

对式（3）取基坑宽度趋向无穷大时的极限，则无限宽时在开挖面以下部分围护结构上的侧向荷载为

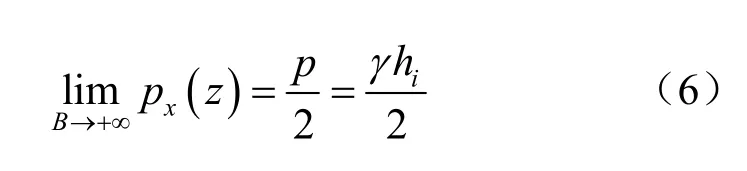
这个结果恰好与前文介绍的日本规范取值方法相一致，说明其具有一定合理性。如果利用式（6）结果，则无限宽基坑开挖时，开挖卸载引起的围护结构上水平荷载可以这样设定：开挖面以上为底宽0.5γhi的三角形荷载，开挖面以下为大小为0.5γhi的矩形荷载。这种荷载模型中，ξ=0.5，具体如图 3(a)所示。如果考虑开挖宽度对坑底以下部分围护上的土压力影响，当基坑为有限宽度时，开挖面以上荷载形式和大小保持不变，开挖面以下随基坑宽度变化，如图3(b)所示。这就是本文提出的考虑基坑宽度的围护结构上的荷载模式。

为分析宽度对围护上荷载的影响，可假定某基坑一次挖深为10 m，土体为饱和黏性土，重度为18 kN/m3，由于土体体积应变较小，泊松比取为0.45。根据上述方法，不同基坑宽度时围护上承受的荷载见图 4。由图可以看出，开挖面以下围护承受的土压力随基坑宽度的增大而增大，荷载形式越来越接近增量法的矩形荷载模式。另外，基坑宽度较小时，坑底附近的荷载明显比墙底大。这将造成基坑宽度越大，墙底水平变形越大，“踢脚”变形更明显，该结果与施工现场经验及文献[5]结论一致。

图4 不同宽度基坑围护上的土压力Fig.4 Earth pressure on enclosure structure of foundation pits with different excavation widths

3 考虑基坑宽度的杆系有限元计算

3.1 采用土压力折减系数调整传统算法围护结构上的荷载

尽管式（3）可以考虑基坑宽度对围护结构上荷载的影响，但在采用杆系有限元方法进行基坑计算时，直接采用图3所示的荷载模式仍然存在一些问题。式（3）是在各向同性的弹性假设基础上推导的结果，与实际土层情况存在一定差异。如果直接应用，势必造成土体重度相同时不同性质土层在基坑形式相同时围护上荷载也相同的结论，这显然是不合理的。式（3）的科学性在于用解析方法得到了能够考虑基坑宽度对围护结构上荷载影响的具体计算方法，比纯粹的经验方法前进了一步。

目前，设计单位最常用的围护结构上荷载是开挖面以上由朗金主动土压力理论计算，开挖面以下为矩形荷载。以此为基础形成大量具有区域经验的被动区土体弹簧刚度，并且在规范中被广泛推荐。基坑变形时，荷载采用朗金土压力计算并不代表围护结构后土层全部进入了主动状态，主要是因为主动区土体侧压力比静止侧压力小，并且随围护结构位移，土压力不断变化；如果围护结构变形一直发展，最终可能会达到主动土压力。实际上，如果考虑这种过程会使算法过于复杂，反而不便于与现场反馈的经验比较。不过，由于采用主动土压力可以考虑土体中能够反映土层性质的黏聚力c和内摩擦角φ，成为目前采用杆系有限元时最常用的取值模式。

为了既能够利用以上提出的考虑基坑宽度影响的荷载计算理论，又能够适应目前基坑设计计算的现状，可采用以下思路：采用上述考虑基坑宽度影响的荷载取值模式，首先计算图3(b)所示的考虑基坑宽度影响的围护结构上荷载总值，再计算图3(a)所示的无限宽基坑的围护结构上荷载总值，以两者之比α(B)作为荷载折减系数对目前传统的围护荷载上荷载进行折减，如图5所示。计算时，只要把折减系数乘到目前广泛采用的矩形荷载模式上就能够考虑基坑宽度对荷载的影响（因为目前广泛采用的矩形荷载模式实际上是基坑无限宽时的荷载），则传统增量法的分步开挖矩形荷载取值变为α(B) pa=α(B)ξγhi。这样，既不过多地改变目前的传统算法，又能够利用现有的基坑计算软件。

下面，基于上面的思路推导考虑基坑宽度影响的荷载折减系数α(B)。

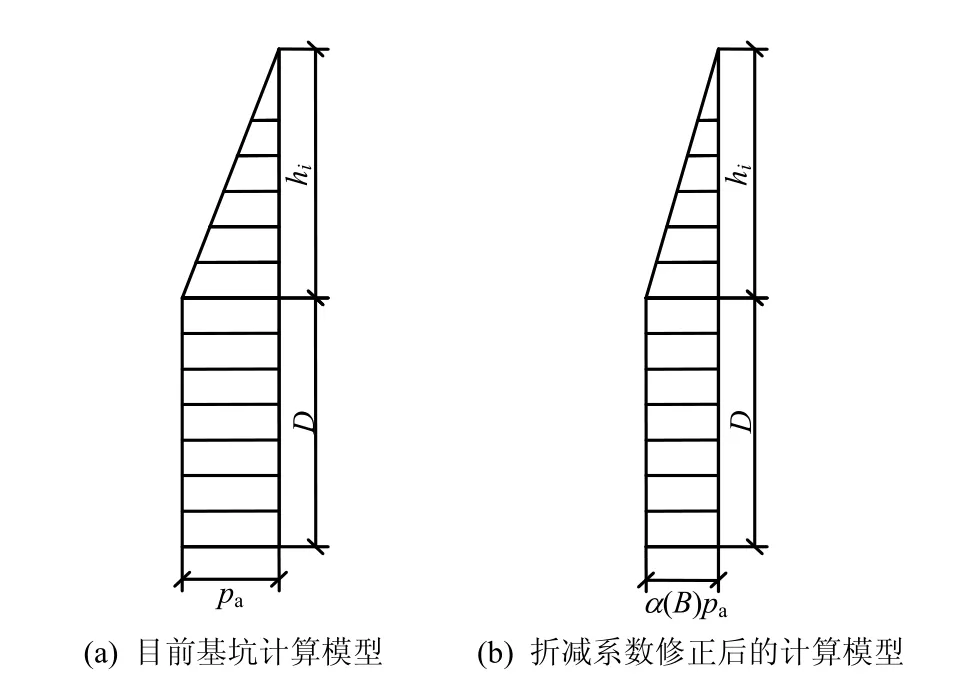
图5 采用折减系数修正目前基坑土压力计算模型Fig.5 Amendments to current earth pressure calculation model of foundation pit by adopting reduction coefficient

3.2 不同宽度基坑围护上土压力折减系数的计算方法

首先，计算图3(b)中图形CDEF的面积，求得开挖面以下部分围护结构上承受的总土压力Pd(B)为

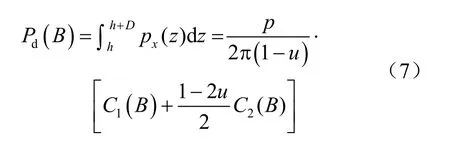
式中：p=γhi，为每层土体开挖产生的竖向荷载；D为围护结构入土深度。且有

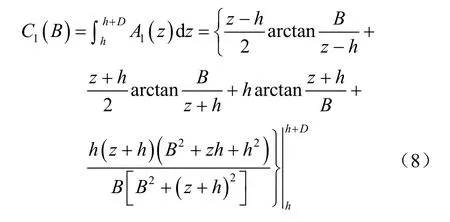
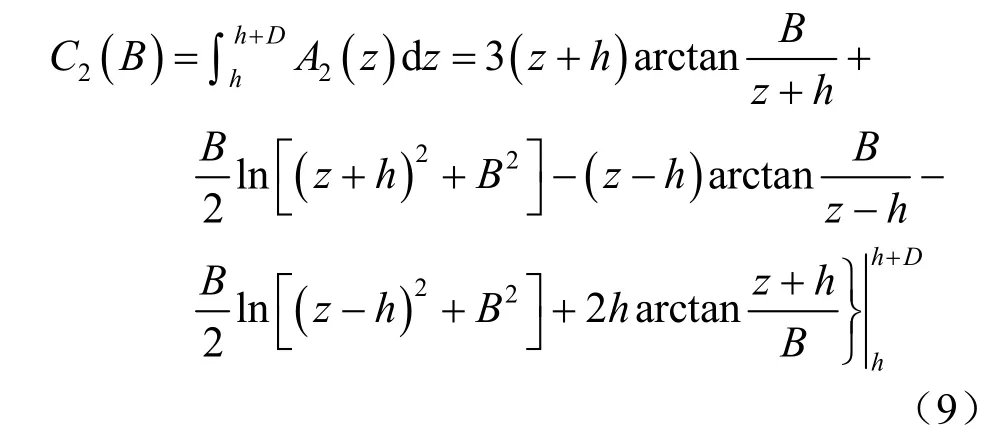
然后，计算每次开挖卸载引起的坑底以上部分围护上的总的土压力 Pu(B )，即图 3(b)中的三角形ΔA BE的面积：

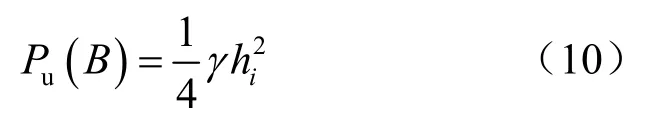
基坑无限宽时，坑底以下部分围护上承受的总土压力 Pd∞(B)为图3(a)中下部分矩形面积：

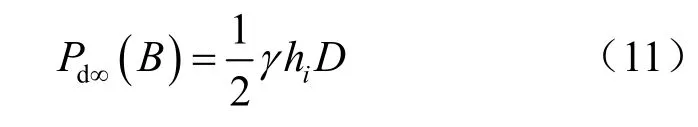
则土压力折减系数α(B)为

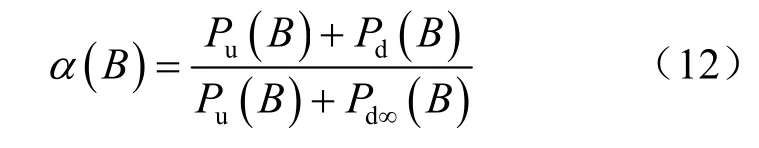
这样，不同宽度基坑的土压力折减系数不同，同一个基坑开挖每层土体时的折减系数也不同。

仍然以前文所述基坑为例。如果基坑的插入深度D分别为10、15、20 m，开挖10 m深基坑的折减系数随基坑宽度变化见图 6。可以看出，围护上土压力折减系数随基坑宽度增加而增大，渐渐趋近于 1。围护插入深度越大，土压力折减系数越小。这种效应在基坑宽度较窄时尤为明显，说明通过增加围护结构插入深度控制变形对窄基坑更为有效。

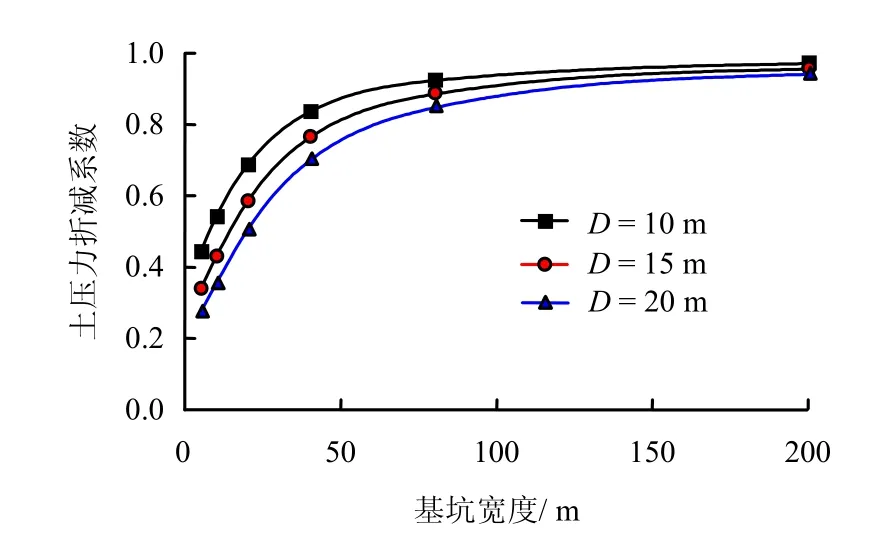
图6 插入深度对土压力折减系数的影响Fig.6 Influence of embedment depth on reduction coefficient of earth pressure

再考虑另一开挖深度为20 m的基坑，围护结构入土深度为20 m。如果每次开挖深度为5 m，共开挖4次。根据本文方法，每次开挖卸载的土压力折减系数见图 7。可以看出，同样卸载量时，随着挖深的增加，土压力折减系数有所增加，但增加幅度不大。因此，计算时可以取各次开挖折减系数的平均值作为每次开挖的平均土压力折减系数。这样，计算方法会变得简便，而且不会造成太大的误差。

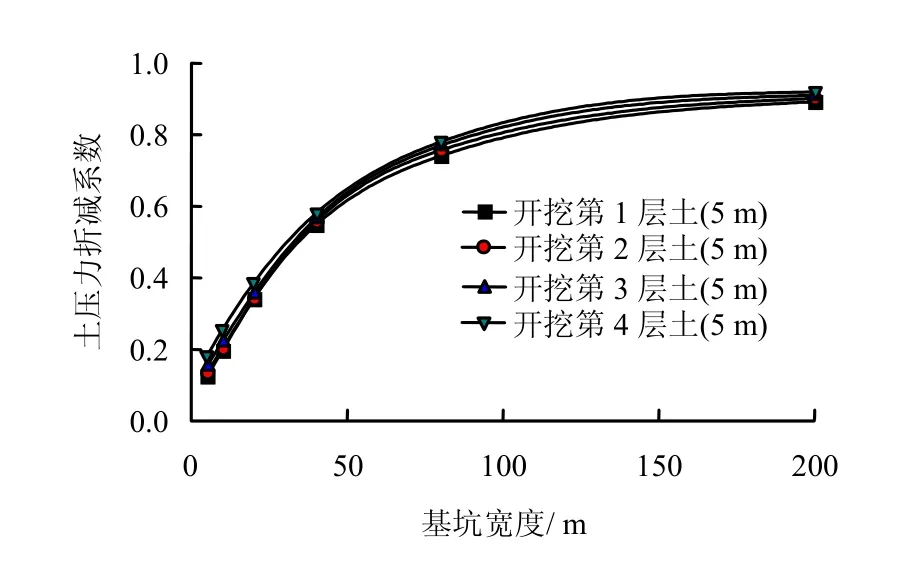
图7 不同开挖步的土压力折减系数Fig.7 Reduction coefficient of earth pressure for different excavation steps

3.3 考虑基坑宽度影响的基坑杆系有限元算法

得到了不同宽度基坑围护上的土压力折减系数，就可以建立考虑基坑宽度影响的杆系有限元算法。计算时，只要计算出不同宽度基坑的土压力折减系数，作为因子乘以传统杆系有限元算法的计算荷载后，再进行有限元计算即可。

如果已知某个地区某宽度基坑实际变形，经过反分析确定被动区土体弹簧刚度后，再计算该地区同样挖深、围护深度的另一宽度基坑时，只要把这个基坑围护的土压力乘以相对土压力调整系数，不需要再调整土层参数和被动区弹簧刚度就可以得到该地区同样挖深、围护深度但宽度不同的另一个基坑的变形。相对土压力调整系数采用下式计算：

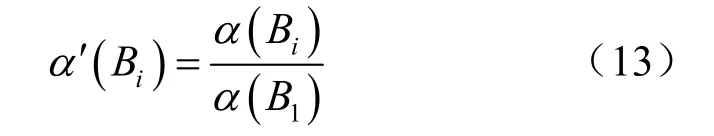
式中：α (B1)为既有基坑的土压力折减系数；α (Bi)为同样挖深和围护深度的另一宽度基坑的土压力折减系数。

4 离心模型试验

尽管施工现场有大量不同宽度基坑监测数据可以参考，但由于现场施工时影响变形的因素众多。即使同样挖深、同样宽度的基坑变形也会不同，难以确定开挖宽度对变形的影响。为此，保持基坑开挖深度、土层情况、围护结构、支撑体系及开挖方式一致，进行3组不同宽度基坑的离心模型试验，以验证本文算法的科学性。

4.1 基坑宽度对变形影响的离心模型试验

试验模拟上海地区的典型土层。试验过程中，保持3组试验的土层基本参数不变，土层物理力学指标见表1。试验模型率N=140，开挖宽度分别选取24、32、42 m进行模拟试验。试验模型均采用半断面形式，被模拟基坑的开挖深度为10 m，围护结构为深22 m、厚800 mm的地下连续墙，采用铝板模拟；竖向共设置3道钢支撑，各道支撑深度分别为0.5、4.0、7.0 m，模拟支撑情况见表2。因为本试验的目的仅是研究不同开挖宽度对基坑变形的影响，开挖支撑次数越多，试验次数越多，试验结果的离散性就越大。为此，试验时在没有施加离心加速度时将土体一次开挖到底，然后施加竖向3道支撑，最后进行离心模型试验。为了保证各次试验结果的可比性，试验用土取自同一地点，试验土制备和土层固结都采用相同方法。

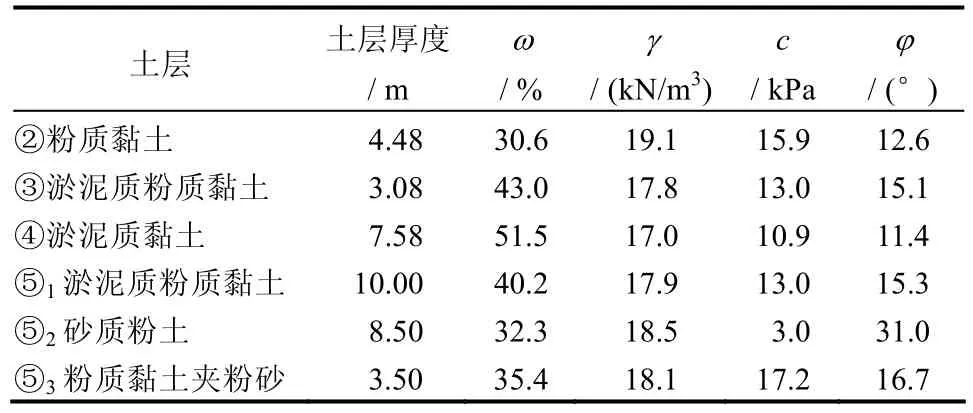
表1 土层主要物理力学参数表Table1 Main physico-mechanical parameters of soil layers

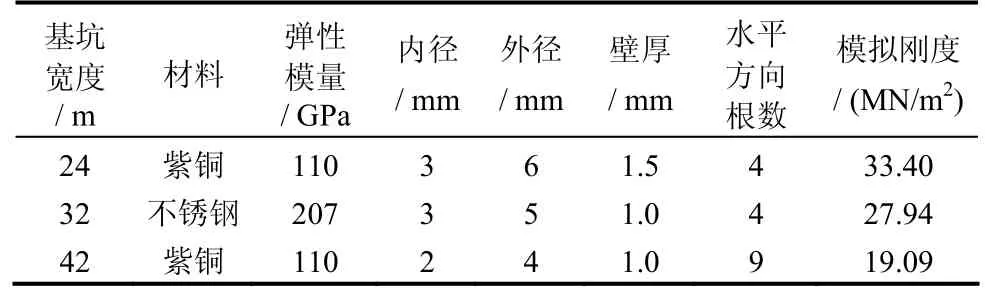
表2 各组试验模型支撑参数Table2 Parameters of supporting structure in each model test

试验时通过同步摄像系统对模型试验的全过程进行监控并拍摄试验模型照片，每组离心模型试验前后的照片见图 8～10。通过图片处理软件分析试验照片经计算得到所需特征点的位移数据，最后得到的围护结构变形曲线见图11。对应宽度为24、32、42 m时的最大变形值分别为27.8、28.5、31.3 mm。可见，随着基坑开挖宽度的增加，连续墙侧向变形量逐渐增大。另外，从图11还可以看出，基坑越宽，围护结构的踢脚变形越大，与施工现场经验相符。

4.2 离心模型试验结果的理论分析

采用本文算法对离心模型试验结果进行分析。首先对第1组试验采用启明星软件进行反分析，调整被动区土体弹簧刚度，得到与第1组试验结果相符的计算结果。然后，采用式（13）计算相对土压力调整系数，对第2组、第3组试验基坑计算时的土压力荷载进行调整；之后，不改变任何其他参数进行有限元计算，就可以得到考虑基坑宽度的杆系有限元计算成果。把应用本文方法的有限元计算成果与离心模型试验结果和传统杆系有限元计算成果（传统算法时只考虑宽度对支撑刚度影响，不考虑宽度对土压力荷载取值的影响）进行对比，见图12。从图中可以看出，传统杆系有限元在计算不同宽度的基坑变形时存在较大误差，并且误差量随基坑宽度增加而增大；而本文方法由于考虑了开挖宽度对围护上土压力的影响，计算结果与试验结果非常接近，说明本文算法有具有一定合理性。

图8 24 m宽基坑的离心试验结果Fig.8 Centrifuge test result of 24 m-wide foundation pit

图9 32 m宽基坑的离心试验结果Fig.9 Centrifuge test result of 32 m-wide foundation pit

图10 42 m宽基坑的离心试验结果Fig.10 Centrifuge test result of 42 m wide foundation pit

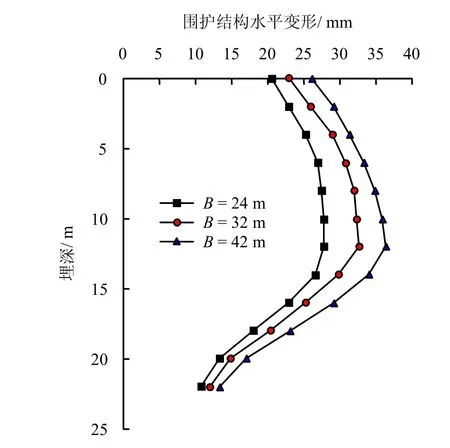
图11 不同宽度基坑变形的离心模型试验结果Fig.11 Centrifuge model test results of deformation of foundation pit with different widths

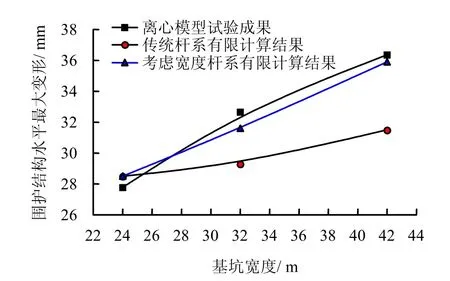
图12 基坑离心试验结果与理论分析成果的对比分析Fig.12 Comparative analysis of centrifuge test results with theoretical analysis results

5 基坑宽度对围护结构变形的影响

采用本文方法可以更科学地研究基坑宽度对变形的影响。保持支撑的布置形式不变，采用本文方法分别针对0.8、1.0、1.2这3个常用的插入比计算模型试验基坑的变形，并与相应的传统杆系有限元计算成果对比，具体见图13。可以看出，传统杆系有限元算法由于没有考虑基坑宽度对土压力影响，在窄基坑时计算的变形过大，会造成偏于保守的设计，这在目前设计中非常常见，而在基坑宽度较大时传统算法的计算结果又偏小，会造成宽基坑设计时偏于危险。以上结果说明，本文算法在狭窄基坑时可以节约资源，在超宽基坑时可以降低工程风险。

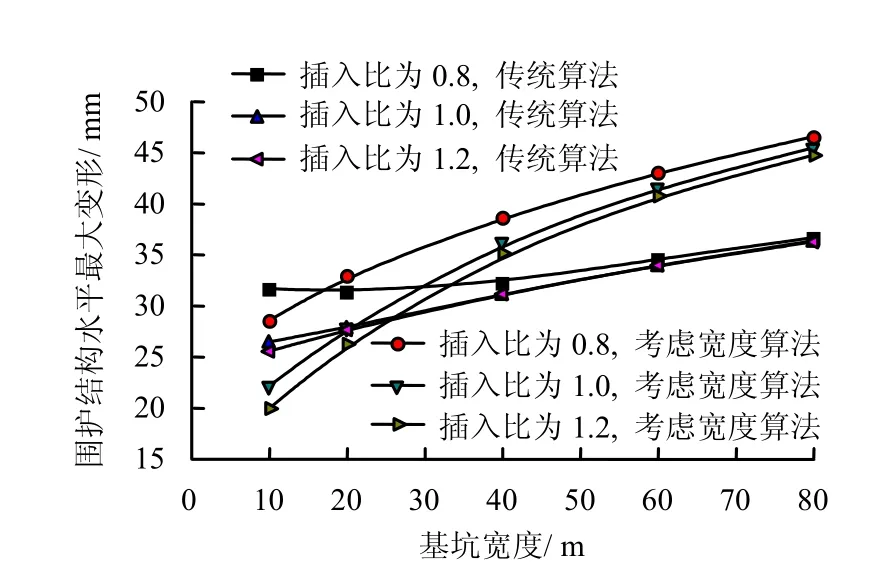
图13 基坑宽度对围护结构水平变形的影响的对比分析Fig.13 Comparative analysis of influence of excavation width on horizontal deformation of enclosure structures

6 讨 论

图3、4显示出狭窄基坑围护结构上荷载与宽基坑时的差异，这种差异会造成宽基坑变形的“踢脚”现象。尽管本文提出的算法能够反映出宽基坑的“踢脚”趋势，但还只是一种为了计算方便及利用现有基坑计算软件的简便算法，这种算法采用了统一的折减系数α(B)对围护上的荷载进行调整，会过小地估计“踢脚”变形。实际上，折减系数α(B)与计算点深度z有关，更精确的计算方法应为

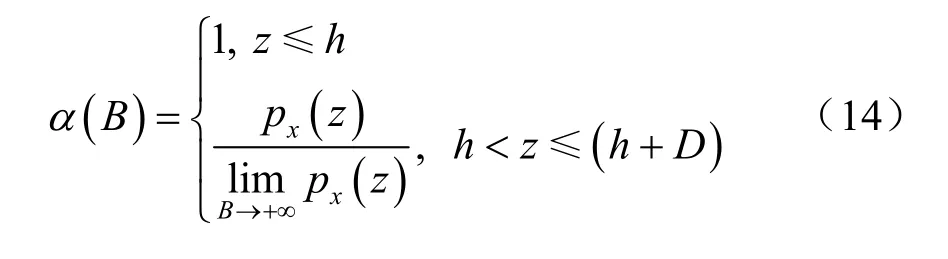
这样，基坑变形计算时，对围护结构上每个深度处土压力分别采用式（14）计算荷载折减系数并进行调整，然后进行有限元计算，即可计算出更接近实际的“踢脚”变形。但这样就无法利用既有的基坑计算软件实现本文算法，需要编制专门的基坑计算软件。

7 结 论

提出了一种能够反映基坑宽度对围护结构上土压力影响的杆系有限元算法，离心模型试验表明该算法更接近工程实际。本文主要结论如下：

（1）传统的杆系有限元基坑计算方法不能全面地考虑基坑宽度对变形的影响，应根据开挖宽度不同对围护结构上的荷载取值进行折减。

（2）通过解析方法得到基坑围护上土压力的折减因子，对传统的基坑围护荷载取值进行调整，改进了传统的基坑杆系有限元算法。

（3）针对不同宽度进行了离心模型试验，试验结果说明开挖条件相近时，基坑越宽围护变形和“踢脚”越大。

（4）采用改进算法的计算结果与离心模型试验结果更加相符，而传统杆系有限元不能够全面反映这种现象。

（5）分析说明采用传统杆系有限元方法设计基坑时，存在着狭窄基坑设计偏于保守，超宽基坑设计偏于危险的问题，而本文算法可以避免该问题。

本文方法是对基坑设计常用的杆系有限元设计方法的修正，希望其他学者采用更多的试验及现场数据对本文理论进行验证，以便在今后基坑设计时推广。

[1]王洪新. 基坑宽度对围护结构稳定性的影响[J]. 土木工程学报,2011,44(6): 120－126.WANG Hong-xin. Influence of excavation width on enclosure-construction stability of foundation pit[J].China Civil Engineering Journal,2011,44(6): 120－126.

[2]张雷,刘振宏,钱元运,等. 深基坑宽度对周围建筑影响的有限元分析[J]. 地下空间与工程学报,2009,5(增刊): 1312－1344.ZHANG Lei,LIU Zhen-hong,QIAN Yuan-yun,et al.Finite element analysis on the effect of different width of deep foundation on buildings around[J]. Chinese Journal of Underground Space and Engineering,2009,5(Supp.):1312－1344.

[3]曾庆义,杨晓阳. 基坑抗隆起稳定问题的应力强度计算方法[J]. 岩土工程学报,1996,18(2): 17－22.ZENG Qing-yi,YANG Xiao-yang. The calculation model for stability of excavation against upheaval[J]. Chinese Journal of Geotechnical Engineering,1996,18(2): 17－22.

[4]胡玉银. 对“基坑抗隆起稳定问题的应力强度计算方法”的讨论[J]. 岩土工程学报,1996,18(6): 119.

[5]应宏伟,聂文峰,郭雷,等. 考虑基坑卸载影响的改进弹性抗力法及其应用[J]. 岩土力学,2011,32(Supp.1):129－133,320.YING Hong-wei,NIE Wen-feng,GUO Lei,et al. A modified beam-spring model method and its application considering unloading effect during excavation[J]. Rock and Soil Mechanics,2011,32(Supp.1): 129－133,320.

[6]张建新. 迭代的增量法分析深基坑中地下连续墙的受力和变形[D]. 上海: 同济大学,2006.

[7]沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社,2000: 88－89.