基于岩饼几何形态测量的原地应力测定方法

李彦恒，谭可可，冯 利

（第二炮兵工程设计研究院，北京 100011）

1 引 言

目前越来越多的地下工程向深部发展，高地应力条件下的工程设计和施工支护需要准确快速测量工程区的原岩三维地应力，而此时钻孔过程中可能会出现岩芯饼化现象，传统的地应力测量方法 （主要是应力解除法）难以实施（见图 1）。《水利水电工程岩石试验规程》[1]章节8.1.1、8.2.1和8.3.1明确提出，应力解除法适用于完整和较完整岩体，其测段内及测段附近岩性应均一完整。《岩石工程试验监测手册》[2]章节3.9.2.2、3.9.3.2和3.9.4.2直接指出，应力解除法在破碎岩体、薄层或出现饼状岩芯处不宜采用。对于传统测量方法，无论是应力解除法，还是水压致裂法，都需要来回地下钻、穿线等繁琐的测量工序和笨重的测量设备，有的方法还需要多个不同方向的钻孔，其结果依赖于传感器、解调仪等大量电子仪器，在地下工程恶劣的测量环境下仪器误差和可靠性都较难控制。本文基于多年来国内外学者对岩饼现象的理论研究，初步提出一种根据岩饼几何形态测量的三维地应力计算方法，实践验证本文方法确定出三维地应力结果合理可靠。

2 国内外岩芯饼化现象的研究进展

岩芯饼化是钻孔过程中特有的岩石力学现象，我国二滩[3]、白鹤滩、拉瓦西等坝址及一些高地应力矿山均有出现。1958年Hast[4]首先报道过岩饼现象，其后 Jeager[5]、Obert 等[6]和 Matsuki 等[7]进行的模拟实验证实高地应力是岩芯饼状破坏的力学原因，认识到主拉应力导致岩芯饼化的力学机制，提出了三维地应力识别的方法。Haimson[8]和Lim[9]分别通过花岗岩的现场和实验室观测，研究了由岩芯破坏模式推测地应力的方法。Li等[10]通过数值模拟，研究了泊松比和岩台（孔底残留的根部岩芯）长度对岩台底部应力集中的影响关系。研究表明，岩饼主平面（2个凸点连线和2个凹点连线所确定的平面）的法线方向和岩芯根部受到的平均赝轴拉应力σsz方向近似平行，其方位角和最小主应力σ3一致，岩饼的外沿高度曲线由三维地应力的方向和钻孔方向决定。计算机模拟实验和现场测量显示岩台长度和岩饼厚度同临界轴拉应力存在定量的关系，结合埋深估计出的垂直应力算出三维地应力的各主应力大小。本文综合国内外学者多年岩芯饼化现象的理论研究成果，结合某深埋地下工程岩饼现象的实例和附近地应力测量资料，初步提出一种根据岩饼几何形态测量来计算三维地应力的方法。

图1 岩饼出现时应力解除法测量被迫中断Fig.1 Overcoring halted because of the occurrence of core disking

3 测量步骤

本方法分3个步骤，即岩饼取样，确定每个岩饼3个主应力的方向，确定每个岩饼3个主应力的大小，详细如下。

（1）岩饼取样

取1.5倍洞径以外典型的原岩岩饼3块以上，记录每个岩饼发生处的埋深，钻孔方向和孔深。

（2）确定每个岩饼三个主应力的方向

①建立XYZ坐标系

如图2所示，钻孔钻进方向为Z轴，最大主应力σ1在Z轴法平面上的投影为X轴，由右手准则确定Y轴；地磁北极到Y轴的夹角为θ0，三维地应力在3个坐标轴上的分量分别为σx、σy、σz。

②建立岩饼外沿高度曲线z和σ1、σ2、σ3三个主应力方向的数学模型（σ3=σz）

当 σ3=σz和 σ1＞σ2时，岩饼外沿的高度曲线z由式（1）给出。

图2 σ3=σz和 σ1＞σ2时岩饼外沿轮廓和XYZ坐标系Fig.2 A surface of a disc with orientations of the maximum and intermediate principal stresses for σ3=σzand σ1＞σ2in the XYZ coordinate system

式中：Am为岩饼外沿高度变化的幅度；θ为岩饼外沿上点在XY平面投影的角度，以正北方向为0°，以逆时针为正，此时σ3的方向和钻孔轴向即Z轴一致，凹、凸面轴分别与σ1即X轴，σ2即Y轴的方向一致，即 θ0=θ2，θ2为σ2的方位角；当σ3≠σz和σ1＞σ2时，岩饼形态的对称性被破坏；为描述岩饼外沿的高度，将图1中建立的XYZ坐标绕X轴旋转α角到 XˊYˊZˊ坐标，再绕 Yˊ轴旋转β角到X〞Y〞Z〞坐标，最终坐标轴 Z〞和σsz的方向一致，这种条件下岩饼外沿的高度z在XYZ坐标系中可由式（2）给出，如图3所示。

式中：R为岩饼的半径；φsz为σsz的倾角；θ3为最小主应力σ3的方位角，也是σsz的方位角，则θ0=仍然成立，各个角度之间有如下关系：

式中：φ2、φ3分别为σ2、σ3的倾角；θ1、φ1分别为σ1的方位角、倾角；ξ为中间变量，其定义为

式中：σm为平均主应力，

根据3个主应力相互垂直的理论要求，当σ2、σ3的方向确定后，σ1的方向也随之确定。

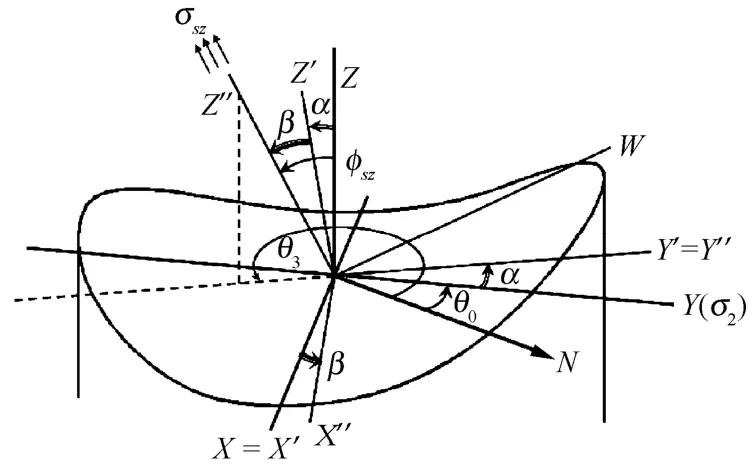
图3 σ3≠σz和 σ1＞σ2时，岩饼外沿轮廓和X〞Y〞Z〞坐标系Fig.3 A surface of a disc for σ3≠σzand σ1＞σ2in the X〞Y〞Z〞coordinate system

③ 测量岩饼外沿高度曲线

以正北方向为0°，以逆时针为正，记录岩饼外沿各点的高度z和角度θ，绘出z -θ高度曲线。

④根据z -θ高度曲线和以下判据确定3个主应力的方向

如果 α=β=0，且Am=0，即岩饼形态呈轴对称，则σ3的方向和钻孔轴向平行，且σ1=σ2；如果α=β=0，且Am≠0，即岩饼形态呈单个平面对称，则σ3的方向和钻孔轴向平行，σ1、σ2的方向垂直于钻孔轴向。利用计算机函数曲线拟合程序找出相应的参数θ0，确定σ1、σ2的方位角。如果α、β有一个不为0或者都不为0，且Am≤ 0.01，即岩饼形态呈单个平面对称，z -θ高度曲线显示的周期近似为360°，则利用函数曲线拟合程序找出最佳的α、β、θ0，再利用式（3）～（7）求出θ3、φ2、φ3，确定相应的θ1、φ1，从而确定出3个主应力的方向；如果α、β有一个不为 0或者都不为 0，且Am≠ 0，即岩饼形态呈单个平面对称，高度曲线显示的周期近似为180°，则利用函数曲线拟合程序找出最佳的Am、α、β、θ0，再利用式（3）～（7）求出θ3、φ2、φ3，确定相应的θ1、φ1，从而确定出3个主应力的方向。

（3）确定每个岩饼3个主应力的大小

根据 3个主应力的方向确定真实的 XYZ坐标系，求出 3个主应力在 XYZ坐标系下的方向余弦li=cosθicosφi，mi=sin θicosφi，ni=sin φi，其中下标i =1，2，3；σx、σy、σz在坐标系XYZ下可由σ1、σ2、σ3来表示：

当岩芯根部区域两个的赝轴拉应力等值面在岩心轴线附近交于一点时，可能产生岩饼，此时岩芯根部的最大平均赝轴拉应力就是临界拉应力σtc，临界拉应力和岩饼产生时岩芯所受三维应力状态的关系为

式中：A、B、C、D分别为岩芯的临界拉应力系数。只有当临界拉应力达到岩石的抗拉强度St时，即

岩饼才能产生。设岩饼产生后，岩台长度为 L，岩饼的半径为R，L与岩饼厚度t有如下关系：

对于确定的岩饼厚度t，根据式（13），L一定，进而可以根据实验室岩石力学数据绘制的岩台长度曲线图中确定岩芯的临界拉应力系数式（11）中的A、B、C、D 四个系数，如图4所示，结合实验室测得的岩石抗拉强度St和式（11），可以得到σx、σy、σz的一个等式（12）。

图4 岩台长度-临界拉应力系数曲线图Fig.4 Critical tensile stress coefficients A,B,C and D as a function of core length

XYZ坐标系确定后，可算出垂直朝上方向在此坐标系中的方向余弦ly、my、ny，对于岩石埋深一定，垂直应力可估算为 σv=ρg h，ρ为岩石的天然密度；g为重力加速度；h为岩饼发生处的埋深，此时垂直应力σv可用σ1、σ2、σ3表示为

由式（8）、（10）、（12）、（14）算出 3 个主应力σ1、σ2、σ3的大小。

以上方法计算出多组的三维主应力大小和方向，最后得到平均地应力的大小和地应力的优势方向。

4 实例验证

某深埋地下工程，巷道毛跨为6 m，岩性为花岗岩，在孔深1.5 m后岩芯饼化严重，见图5，取孔深12 m以外的典型岩饼（R = 5.4 cm），岩饼厚度平均为2.2 cm，由此计算出的岩台长度L = 15.567 mm，对应的临界拉应力系数为 A = 0.244，B =0.289，C = 0.0001，D = 0.136。根据巴西圆盘试验结果，发生岩饼的岩石抗拉强度为13.5 MPa，钻孔方位角为341°，倾角为86°。测得其中3块岩饼的外沿高度曲线如图6所示，表1为由高度曲线得到的中间参数值。

图5 在某深埋工程实施的应力解除法钻孔过程中岩芯饼化现象严重Fig.5 Photographs of serious core disking obtained from overcoring borehole

根据式(3)～(10)及3个主应力相互垂直，由中间参数和临界拉应力系数算出各主应力方向，再根据式（8）、（10）、（12）、（14）可以计算出 3 个主应力大小。表2为同附近（没有岩芯饼化处）应力解除法地测得的地应力结果对比。由表可见，这种初步计算方法得到的地应力方向同应力解除法相比，倾角差别较小，最大为7°，方位角相差不大，最大约为17°，测出的3个主应力值大于应力解除法的值，因为根据《工程岩体分级标准》[11]中岩饼出现的条件为σc/σ1=3～6，σc取220 MPa，则σ1=36.7～73.3 MPa，未发生岩饼能够使用应力解除法的区段最大主应力不在这个范围内，岩饼法测算出的最大主应力符合这一条件，说明该方法测量出的地应力大小和方向都是合理可靠的。

图6 岩饼的z-θ高度曲线和由式(2)拟合曲线Fig.6 Comparison of the height distribution at the periphery of the end surface of discs with that determined by fitting Eq. (2)

表1 计算参数Table1 Calculation parameters

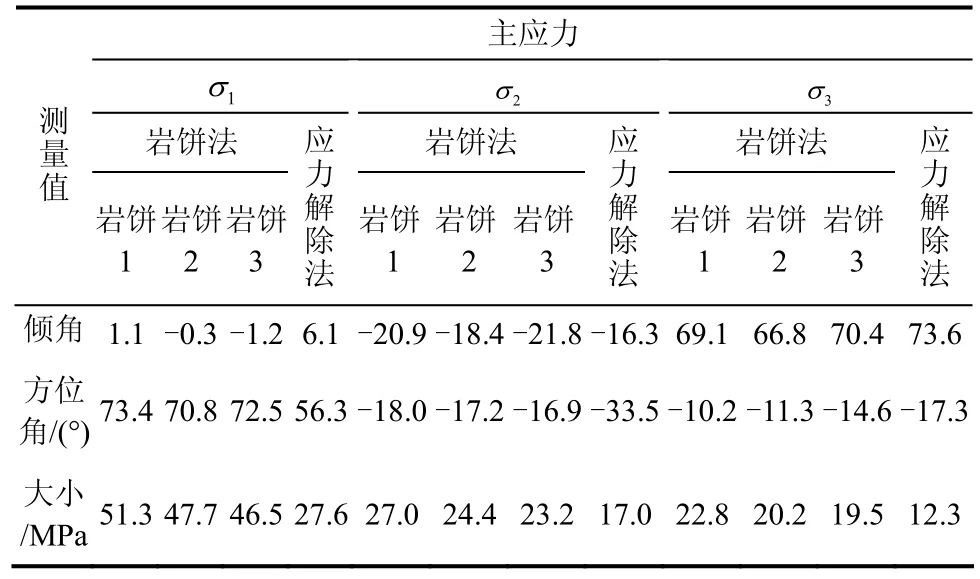
表2 岩饼法测得地应力方向和大小与应力解除法的结果对比Table2 Comparison of directions and values of 3D stress from core disking with those from overcoring method

5 结 语

由于岩饼的形成和地应力状态密切相关，采用岩饼形态测量计算出地应力的方法，直接捕捉到了更多的地应力信息，测得的地应力值更接近于原岩真实地应力值。同时，这种初步计算方法可以解决岩饼持续出现时传统地应力测量方法（主要是应力解除法）不能测定原岩地应力的问题，经实例验证，使用本方法确定出三维原岩地应力大小和方向合理可靠，并具有简便、实用的优点。

[1]长江科学院. SL264－2001水利水电工程岩石试验规程[S]. 北京: 中国水利电力出版社,2001.

[2]林宗元. 岩土工程试验监测手册[M]. 北京: 中国建筑工业出版社,2005.

[3]白世伟,李光煜. 二滩水电站坝区岩体应力场研究[J].岩石力学与工程学报,1982,1(1): 45－56.BAI Shi-wei,LI Guang-yu. Study on stres field of rock mases in the dam site of Ertan hydropower station[J].Chinese Journal of Rock Mechanics and Engineering,1982,1(1): 45－56.

[4]HAST N. The state of stresses in the upper part of the earth’s crust[J]. Engineering Geology,1958,2(1): 5－17.

[5]JAEGER J C,COOK N G W. Pinching off and discing of rocks[J]. Journal of Geophysical Research,1963,68(6):1759－1765.

[6]OBERT L,STEPHENSON D E. Stress conditions under which core discing occurs[J]. Society of Mining Engineers,1965,232(3): 227－235.

[7]MATSUKI K,KAGA N,YOKOYAMA T,et al.Determination of three-dimensional in-situ stress from core discing based on analysis of principal tensile stress[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(7): 1167－1190.

[8]HAIMSON B,LEE M Y. Estimating deep in-situ stresses from borehole breakouts and core disking—Experimental results in granite[C]//Proceedings of the International Workshop on Rock Stress Measurement at Great Depth,the 8th International Congress on Rock Mechanics. Tokyo:[s. n.],1995: 19－24.

[9]LIM S S,MARTIN C D. Core disking and its relationship with stress magnitude for Lac du Bonnet granite[J].International Journal of Rock Mechanics and Mining Sciences,2010,47(2): 254－264.

[10]LI Y Y,SCHEMITT D R. Effects of Poisson’s ratio and core slab length on bottom hole stress concentrations[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(5): 761－773.

[11]中华人民共和国水利部. GB 50218－94工程岩体分级标准[S]. 北京: 中国计划出版社,1994.