顺层岩质边坡地震动力响应研究

言志信，高 乐，彭宁波，任志华，郭 斌

(1. 兰州大学 土木工程与力学学院，兰州 730000；2. 兰州大学 西部灾害与环境力学教育部重点实验室，兰州 730000；3. 云南省公路科学技术研究院，昆明 650051)

1 引 言

强烈地震触发的滑坡、崩塌、泥石流等地质灾害，特别是在山岳地区，其危害程度往往比地震直接造成的危害更大。从发生的数次典型地震的致灾的统计数据看，强烈地震触发的斜坡崩、滑、流等地质灾害造成的人员伤亡数量占到地震伤亡总人数的1/3甚至更多，其危害程度不亚于一场大地震。据统计，四川汶川8.0级地震触发了15000多处滑坡、崩塌、泥石流等地质灾害，估计直接造成2万人死亡。地质灾害隐患点达12700多处，以崩塌体灾害增加最为显著，威胁近百万人的生命安全[1]。

地震是地球内能的释放，它是以波动的形式传播的。地震震级和震源深度是描述地震最基本的物理量，震级越大、震源越浅则地震造成的破坏越大。一般认为，竖向的运动是最先到达的P 波引起，水平向运动是P 波之后的S 波及其次生的面波引起，因此，地震发生后最早是竖向地震动较水平运动强烈，而后由于 S 波到达而逐渐变为水平向运动强烈，此时竖向运动相对较弱。在P 波行将结束而S波即将或已经到来时，则两者幅值较低且接近。显然，超过一定阈值的强烈的水平向地震动和竖向地震动的时差取决于震源深度、震中距离及地震波在地层传播过程中的衰减。距离震中越近，两者的时差越小，共同出现较高加速度的几率也越高，产生的破坏也就越强烈[2]。

边坡地震动力响应是指地震所引起的边坡反应，包括地震动在边坡中引起的加速度、速度、位移等[3]。边坡动力响应问题既是一个古老也是一个年轻的命题，是近年来工程地质、岩土工程、地震工程领域的研究热点。边坡的动力响应涉及多学科交叉的问题，同时涉及地震学、地球物理学、地震工程学等学科的内容，目前的研究还很不成熟。

在以往地震作用触发的斜坡崩滑效应分析中，对水平地震力作用考虑较多而往往忽视了竖向地震力作用，而据多次典型地震的灾后实地调查结果，都表明竖向地震动十分明显，尤其在强震的震中附近，竖向与水平向地震动加速度之比为 0.5～2.4，其平均值接近于 1[4]。由于震中附近的地震波几乎竖直出露地表(纵波的质点振动方向同轴于波前进方向，交替地挤压和拉张其穿越的岩土体；横波的质点振动方向垂直于波前进方向，反复剪切其穿越的岩土体)，故竖向加速度几近全由地震竖向波产生，而水平向加速度几近全由地震水平向波产生。随着震中距的增加，地震波多以一定的入射角出露地表，此时地震竖向和水平向波则分别产生各自的竖向、水平向加速度[5]。在进行地震动力作用触发的斜坡崩滑效应分析时，需要综合考虑水平和竖向加速度的耦合作用，这是本文突破传统斜坡动力响应分析中仅考虑水平地震力作用的局限而体现出创新性。

2 顺层岩质边坡分析模型

2.1 边坡概况

如图1所示，一高30 m、坡角60°的顺层岩质边坡，岩层1为强风化岩，岩层2为微风化岩，岩层3为完整岩体，两结构面倾角均为41°。岩体的物理力学参数如表1所列。

图1 顺层岩质边坡示意图（单位：m）Fig.1 Stetch of a bedding rock slope(unit: m)

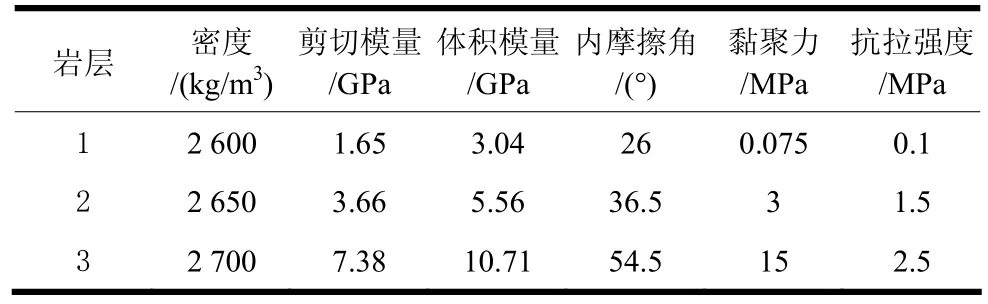
表1 岩体物理力学参数Table1 Physico-mechanical parameters of rock masses

2.2 计算模型

本文利用FLAC3D进行有限差分动力分析，岩体材料采用弹塑性本构模型和Mohr-Coulomb强度准则，两侧设置自由场边界，从而有效地避免向外传播的地震波反射回模型内部和能量发散，施加局部阻尼，阻尼系数为0.156[6]，先通过静力计算达到平衡状态，再施加预设动力边界条件进行分析。本算例计算边界：坡脚到右端边界的距离是坡高的1.5倍，坡顶到左端边界的距离是坡高的2.5倍，上下边界总高是坡高的2倍，边界范围满足计算精度要求[7]。

2.3 监测点设置

为描述地震作用下边坡加速度响应规律，在模型坡面上设置监测点（见图1），并定义任意一点动力响应加速度峰值与坡脚监测点加速度峰值的比值为PGA放大系数[8]。在坡面上按一定间距选取A～G共7个监测点进行监测。通过分析顺层岩质边坡各监测点在不同地震荷载下 PGA放大系数和横向最大位移和塑性区变化，得到边坡在地震作用下 的动力响应规律，分析顺层岩质边坡在不同地震波作用下的抗震效果。

图2 地震波作用下数值模型边界条件示意图Fig.2 Boundary condition of model subjective to seismic loads

2.4 动力条件的输入

本文选取Kobe折减波（Nishi-Akashi监测站）作为地震动输入，竖向地震波峰值加速度调整为0.066g，进行滤波和基线校正后输入持续时间为18 s，调整后地震竖向波加速度时程曲线如图3所示。水平向地震波峰值加速度调整为0.124g（相当于Ⅶ度基本烈度[9]），进行滤波和基线校正后输入持续时间为18 s，调整后地震水平向波加速度时程曲线如图4所示。

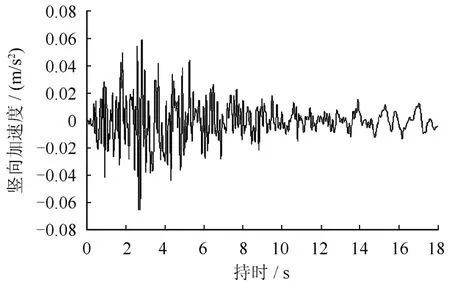
图3 计算中输入的地震竖向波加速度时程曲线Fig.3 Time-history curve of seismic wave acceleration in vertical direction

图4 计算中输入的地震水平向波加速度时程曲线Fig.4 Time-history curve of seismic wave acceleration in horizontal direction

地震波时差作用是指由于地震纵横波速的差异导致其到达特定斜坡体存在时间差 Δt（见式（1）），特指从竖向地震波到达斜坡体到水平向地震波到达斜坡体的时间区间，该时间段内斜坡体仅受竖向地震波的个体周期拉压作用,而当水平向地震波到达斜坡体后，斜坡体开始受竖向地震波的周期拉压和水平波向地震波的周期剪切耦合作用，即地震波耦合作用。

式中：r为震源距；VP为竖向地震波波速；VS为水平向地震波波速。

监测站距离震中淡路岛北部约7.1 km（淡路岛北部附近震源深度约为 17.9 km，震源距为 19.3 km），地震竖向和水平向波波速（竖向波传播速度VP≈6，水平向波传播速度VS≈3.5[9]）竖向和水平向波时间差约2.29 s（由式（1）得出），即在模型底部先输入竖向波产生的竖向加速度，2.29 s后再输入水平向波产生的水平加速度，据此分析顺层岩质边坡模型在个体及耦合力条件作用下的动力响应规律。

边坡的动力响应包括加速度、速度、位移、动应力和动应变响应等，加速度响应及其分布规律是评价边坡地震动力响应的基本资料[10]，动力作用下边坡可能发生的残余变形也是工程最关心的问题。本文主要从位移和加速度来研究顺层边坡的动力响应规律。

3 动力响应分析

3.1 耦合条件下位移场分布

如图5所示，边坡受耦合波作用时的坡面监测点横向最大位移，对比仅受水平向波边坡的最大位移响应，仅受水平向波时，坡面横向最大位移在结构面附近，达11.6 cm；受耦合波时，结构面附近的坡面最大水平位移达 18.9 cm，最大水平位移增大了 62.9%，这说明竖向地震力对边坡造成了极大的破坏作用，单纯的模拟水平振动，忽视竖向振动并不能完全的反应边坡的动力响应，误差是很大的。从图5中也可以得出，两种情况下边坡的最小位移都出现在坡脚处，仅受水平向波时为5 cm，受耦合波时为4.1 cm，最小水平位移减小了18%。此外，笔者还发现了另一个现象，仅受水平向波作用时，结构面以下位移缓慢增长，数量级为0.1 cm，而耦合波作用下，结构面以下坡面的位移增长数量级为0.001 cm，几乎没有增长，认为这都是因为结构面的存在，竖向波和水平向波及其地质界面的反射波之间发生干涉，使竖向波和水平向波振幅均减小。这个由波的入射角，相位差等因素决定。

图5 两种情况下坡面各点X方向最大位移Fig.5 Maximum horizontal displacement of points along slope surface under two kinds of earthquakes

3.2 耦合条件下加速度场分布

从图6可以看出，仅受水平向波情况下和受耦合波情况下，边坡坡面的PGA整体变化规律一致，均在结构面处出现一突变，但耦合波作用下的PGA系数大于仅受水平向波条件下，说明竖向波造成的竖向振动，加重了斜坡体内部的损伤，岩体强度有所减弱。从图 7中可以看出,坡面水平向和竖向PGA放大系数均随高程增大，在结构面处有一突变，在坡顶处也明显增大，加速度响应规律显示了坡体对输入地震波的垂直放大作用和临空面放大作用，这与徐光兴[7]等的结论相吻合，是由于在结构面和坡顶附近入射波和反射波叠加效应所致，且与垂直放大效应也有关系。同时，这个原因也导致了整体PGA放大系数的细微波动。

图6 两种情况下坡面各点PGA放大系数Fig.6 Coefficients of amplification for PGA of points along slope surface under two kinds of earthquakes

图7 坡面监测点水平向和竖向PGA放大系数变化图Fig.7 Coefficients of amplification for PGA of pionts along slope surface in vertical and horizontal directions

3.3 耦合条件下塑性区变化

图8为顺层岩质边坡在仅受水平向波和耦合波情况下塑性区图。对比两种情况可以得出，塑性区主要表现为剪破坏和拉破坏，大部分单元是在剪拉共同作用下产生破坏，说明地震波产生的水平与竖向拉裂耦合作用是触发斜坡体产生初期崩滑破坏的主控因素，而耦合波情况下比仅受水平向波多出一个剪拉共同作用单元，说明耦合情况下水平与竖向拉裂耦合作用更加明显，对边坡的破坏作用更加明显，更加符合实际情况。

图8 两种情况下边坡塑性区分布Fig.8 Plastic zone under two kinds of earthquakes

3.4 耦合条件下加速度、速度动力响应规律

为研究边坡在耦合波作用下的动力响应规律，笔者在模型中坡体内竖直方向布置监测点，考察边坡的动力响应的速度放大系数及加速度放大系数沿坡体竖直方向和水平方向的变化规律。

从图9可以发现，耦合地震波作用下斜坡体内部的V1～V7剖面上的水平、竖向速度，水平、竖向加速度随高程的增加均产生了不同程度的放大效应。其中竖向加速度的放大效应最为明显，在接近坡面处，其放大倍数约为6.80。放大系数值从大到小依次是：竖向加速度＞水平加速度＞竖向速度＞水平速度，同时说明在水平方向上距坡面一定深度范围内加速度的响应具有趋表效应，这也与董金玉等[11]的研究成果相吻合。

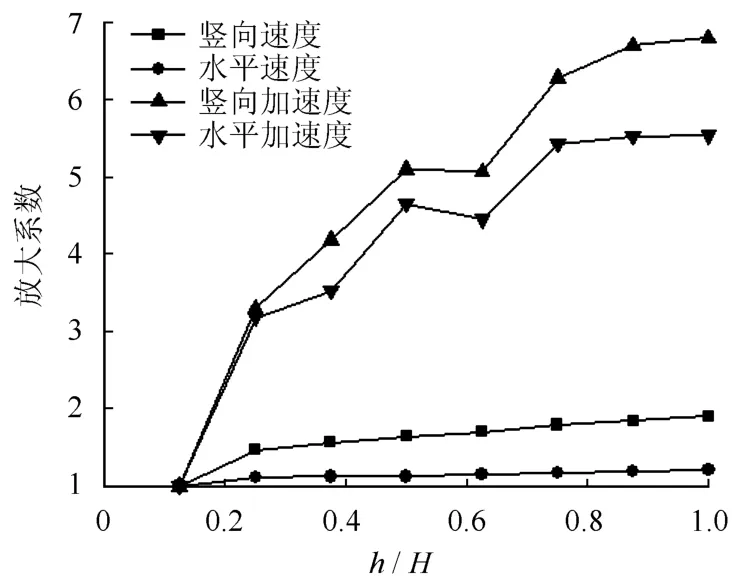
图9 坡体内部剖面参数放大系数Fig.9 Magnification factors of parameters in profile V1-V7

4 折减波aV/aH对边坡动力响应的影响

顺层岩质边坡在耦合波作用下的动力响应，除了受波形，加速度峰值，频率和持时的影响外，还有一其独有的影响因素，即地震峰值竖向加速度与峰值水平加速度之比 aV/aH。本文在接下来讨论这一因素对顺层岩质边坡的影响。

选取的kobe折减波av/aH= 0.53，模拟工况下整体调整P波，放大其峰值加速度，使其aV/aH分别为0.75、1.25和1.75，持时18 s。

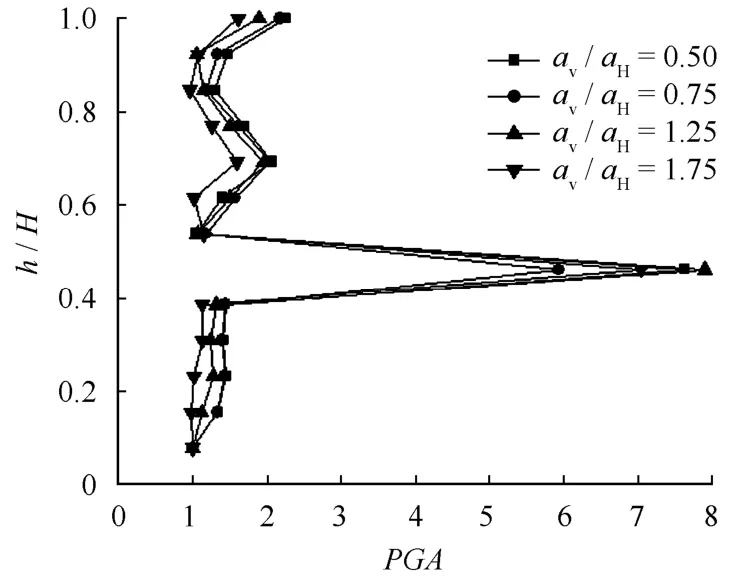
图10 不同av/aH坡面各点PGA放大系数Fig.10 Coefficients of amplification for PGA of points along slope surface in different values of aV/aH

从图 10可以看出，3种情况下边坡水平向PGA放大系数变化趋势基本相同，在坡脚和结构面之间缓慢增加，在结构面处突然增大，在坡顶处也明显增大，说明耦合波作用下aV/aH对边坡水平向加速度影响不明显，水平向加速度受峰值和结构面位置影响较大。从图11可以看出，随着aV/aH的增大，坡面各点横向最大位移基本呈增大趋势。随着aV/aH的增大，结构面位置的最大横向位移的突变现象被放大，且结构面以上各点之间最大位移突变较大，说明地震波产生的水平与竖向拉裂耦合作用是触发斜坡体产生初期崩滑破坏的主控因素，竖向地震作用起了重要的破坏作用，而 aV/aH越大，破坏越剧烈也印证了许多地震工作者发现极震区竖向地震力起破坏作用。图12为不同av/aH坡面塑性的分布。分析4种情况下边坡的塑性区图对比可以发现，随着 aV/aH的增大，剪拉共同作用单元数量也随之增加，表明对顺层岩质边坡的破坏效应也逐渐增大，且在aV/aH= 1.75时发现有一个拉剪共同作用单元，又重新进入了剪切破坏状态，也说明在地震中竖向地震力起了重要的破坏作用。

图11 不同aV/aH坡面各点X方向最大位移Fig.11 Maximum horizontal displacement of points along slope surface in different values of aV/aH

图12 不同aV/aH坡面塑性区分布Fig.12 Plastic zone in different values of aV/aH

5 结 论

(1) 竖向和水平向地震波耦合作用模拟比单纯模拟水平振动对岩土体的破坏更大，更加接近实际情况。由于结构面的存在，竖向波和水平向波及其地质界面的反射波之间发生干涉，使竖向波和水平向波对斜坡体造成的影响产生了一定程度的变化。

(2) 顺层岩质边坡在地震波耦合作用下存在垂直放大和临空面放大作用；坡面水平向和竖向加速度在竖直方向随高程增加呈增大趋势，在结构面出增大特别明显。

(3) 地震纵波产生的水平与竖向拉裂耦合作用是触发斜坡体产生初期崩滑破坏的主控因素，而耦合情况下水平与竖向拉裂耦合作用对边坡的破坏更加明显；

(4) 该斜坡体动力响应特征值的放大效应表明，其放大系数值从大到小依次是：竖向加速度＞水平加速度＞竖向速度＞水平速度，该结果与斜坡体发生破坏的形成机制及主控因素相符，即地震竖向波产生的竖向加速度起到了优势破坏作用。

(5) 地震耦合波作用下，随着aV/aH的增大，坡面各点横向最大位移基本呈增大趋势，说明地震波产生的水平与竖向拉裂耦合作用是触发斜坡体产生初期崩滑破坏的主控因素，竖向地震作用起重要的破坏作用，而 aV/aH越大，破坏越剧烈，也印证了许多地震工作者发现极震区竖向地震力起破坏作用。

[1]郑颖人,叶海林,黄润秋,等. 边坡地震稳定性分析探讨[J]. 地震工程与工程振动,2010,30(2): 173－180.ZHENG Ying-ren,YE Hai-lin,HUANG Run-qiu,et al.Study on the seismic stability analysis of a slope[J].Journal of Earthquake Engineering and Engineering Vibration,2010,30(2): 173－180.

[2]殷跃平. 汶川八级地震地质灾害研究[J]. 工程地质学报. 2008,16(4): 433－444.YIN Yue-ping. Researches on the geo-hazards triggered by Wenchuan earthquake,Sichuan[J]. Journal ofEngineering Geology,2008,16(4): 433－444.

[3]徐光兴,姚令侃,李朝红,等. 边坡地震动力响应规律及地震动参数影响研究[J]. 岩土工程学报,2008,30(6):918－923.XU Guang-xing,YAO Ling-kan,LI Zhao-hong,et al.Dynamic response of slopes under earthquakes and influence of ground motion parameters[J]. Chinese Journal of Geotechnical Engineering,2008,30(6): 918－923.

[4]林淋. 竖向地震动特征分析[D]. 哈尔滨: 中国地震局工程力学研究所,2005.

[5]翟芳鹏. 地震 P-S波时差耦合作用的斜坡崩滑效应研究[D]. 北京: 中国科学院地质与地球物理研究所,2009.

[6]Itasca Consulting Group. FLAC3D Version 4.0 (fast lagrangian analysis of continua in 3 dimensions) User’s manual[M]. USA: Itasca Consulting Group,2009.

[7]郑颖人,赵尚毅,张鲁渝. 用有限元强度折减法进行边坡稳定分析[J]. 中国工程科学,2002,4(10): 57－62.ZHENG Ying-ren,ZHAO Shang-yi,ZHANG Lu-yu.Slope stability analysis by strength reduction FEM[J].Engineering Science,2002,4(10): 57－62.

[8]祁生文,伍法权. 岩质边坡动力反应[M]. 北京: 科学出版社,2007.

[9]胡聿贤. 地震工程学[M]. 北京: 地震出版社,1988.

[10]徐光兴,姚令侃,高召宁,等. 边坡动力特性与动力响应的大型振动台模型试验研究[J]. 岩石力学与工程学报,2008,27(3): 624－632.XU Guang-xing,YAO Ling-kan,GAO Zhao-ning,et al.Large-scale shaking table model test on the dynamic characteristics and seismic responses of slope[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(3): 624－632.

[11]董金玉,杨国香. 地震作用下顺层岩质边坡动力响应和破坏模式大型振动台试验研究[J]. 岩土力学,2011,32(10): 2977－2983.DONG Jin-yu,YANG Guo-xiang. The large-scale shaking table test study of dynamic response and failure mode of bedding rock slope under earthquake[J]. Rock and Soil Mechanics,2011,32(10): 2977－2983.