锥导乘波体气动代理建模方法研究

王烁, 李萍, 陈万春

(北京航空航天大学 宇航学院, 北京 100191)

锥导乘波体气动代理建模方法研究

王烁, 李萍, 陈万春

(北京航空航天大学 宇航学院, 北京 100191)

传统的气动计算方法计算繁琐、计算效率低,不适应于乘波体多学科设计优化,通过建立气动代理模型可以很好地解决气动计算精度和效率的矛盾。利用面元法进行气动估算,采集了锥导乘波体在设计点、非设计点的气动特性作为训练数据,构建了Kriging和LS-SVM代理模型,对比了两种模型对此高维问题的代理效果。结果表明,Kriging代理模型能更准确地表达锥导乘波体的气动特性,应用代理模型进行优化等工作的计算效率与传统气动计算方法相比有显著的提高。

锥导乘波体; 气动特性; Kriging; LS-SVM; 代理模型

引言

乘波体因具有更大的升阻比[1]和更好的气动特性[2],以其作为新一代高超声速飞行器布局进行的多学科设计优化(Multi-discipline Design Optimization, MDO)备受瞩目。目前对乘波体的优化工作大多是建立在计算流体力学[3]或气动估算[4-5]基础上的单学科或少数学科的一体化设计。这两种方法都不适用于MDO过程,因其具有以下缺点:(1)计算工具不是为MDO设计的,因而数据传输困难;(2)计算准备工作繁琐,不适宜反复计算;(3)计算效率低。以牛顿面元法[6-7]为代表的气动估算与CFD方法相比虽然效率有所提高,但仍不适用于MDO过程中大量的实时计算。而代理模型可以很好地解决计算精度与效率的矛盾,是MDO过程的有力工具。基于插值技术的Kriging模型[8]和基于拟合技术的LS-SVM模型[9]是两类具有代表性的代理模型。本文以锥导乘波体气动学科为例,建立了其两种代理模型,讨论了它们对高维设计空间代理的效果。结果表明,Kriging代理模型能更准确地描述锥导乘波体的气动特性,更适合高维问题的代理,应用其进行优化等工作的计算效率有显著提高。

1 数学描述

1.1 锥导乘波体生成过程

(1)锥形流场解算。锥形流场虽然由一个轴线平行于来流方向的细长圆锥诱导,但对于锥导乘波体外形起决定作用的是激波的半锥角[10],因此本文直接选取半锥角为设计参数,求得自由流经斜激波后的流动参数,并解算Taylor-Maccoll方程[11],该方程在任意过激波锥母线的平面内可简化为:

(1)

上式中各参数的定义见文献[10]。采用4阶Ronge-Kutta法求解上式可得精度较好的流场。

(2)确定形状曲线并生成上表面。形状曲线选取由4个控制点确定的3度Bezier-Bernstein曲线,本文选取的4个控制点如表1所示。

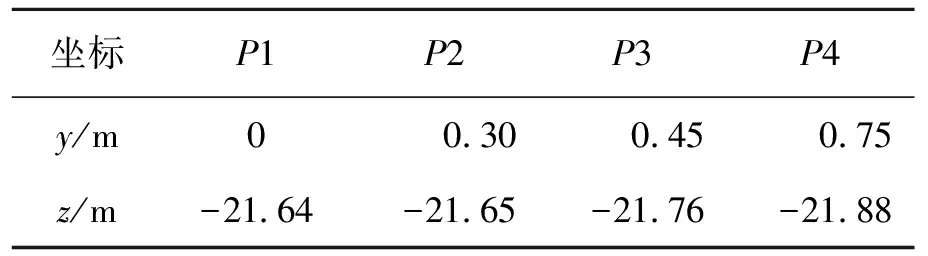
表1 3度Bernstein曲线控制点

将曲线上各点沿自由流线逆向追溯到锥形激波表面,交点则组成锥导乘波体的前缘曲线,同时可得乘波体的上表面。这种自由流上表面是最易于计算的,为了进一步改善乘波体升力特性,也可将上表面设计成具有膨胀角的外形。

(3)流线追踪生成下表面。以前缘曲线上的各点为起始点,顺流追踪激波后锥形流场中的流线至乘波体的底部,则可以形成锥导乘波体的下表面。本文研究的锥导乘波体生成示意图和基本外形分别如图1和图2所示。以基本外形为基础,通过改变设计马赫数Macfg、设计激波半锥角βcfg和设计高宽比H/W这3个参数,可以得到一系列外形,如图3所示。

图1 锥导乘波体生成示意图

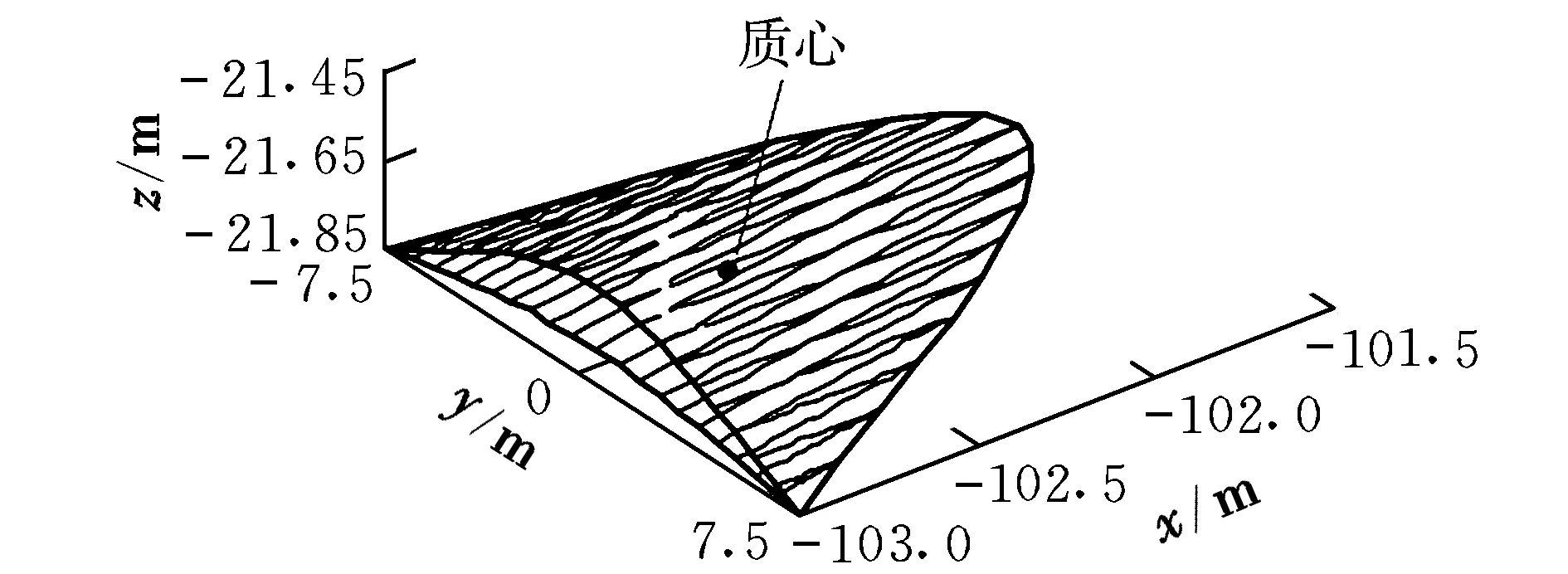
图2 基本外形

图3 改变外形参数得到的锥导乘波体

1.2 Kriging代理模型

Kriging模型最早由Sacks等[8]提出,其是将真实模型响应描述为零均值平稳高斯随机过程,以相关函数为权值进行插值,因此不仅可以给出预测值,还可以给出预测方差。其表达式为:

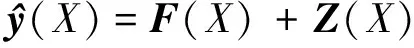
(2)

式中,F(X)=βTf为响应确定性部分；βT={β1,β2, …,βp}为回归系数向量；fT={f1,f2, …,fp}为低阶多项式回归函数向量;Z(X)是零均值方差为σ2的随机过程,具有如下协方差矩阵:

Cov[Z(Xi),Z(Xj)]=σ2[Rij(Xi,Xj)]

(3)

式中,Xi和Xj为设计空间中的两点,i≥1，,j≤N,N为预测点总数。相关函数矩阵中的元素为:

(4)

式中,Rk为具体形式的相关函数,有多种常用形式,常用的高斯相关函数为:

(5)

1.3 LS-SVM代理模型

最小二乘支持向量机 LS-SVM是由Suykens[9]于1999年提出的,属于机器学习范畴,是一种针对未知结构的统计预测方法。设有训练数据Xi=(xi,yi),需要找到某种映射关系f:x→y,同时使风险指标R(f)达到最小。

(6)

式中,L为损失函数,表示预测与真实值的偏离程度。映射可以表示为：

f(w,x)=wTΦ(x)+b

(7)

式中,w为系数矢量;Φ为x的未知函数矢量。回归分析转化为凸二次优化问题:

(8)

(9)

于是

(10)

SVM用核函数来表示未知函数的乘积,即:

K(x,y)=Φ(x)Φ(y)

(11)

至此,完成了在高维特征空间的线性回归。

2 气动特性代理

本文锥导乘波体的基本外形参数选取为:Macfg=10,βcfg=12°,H/W=0.16,设计飞行高度Hcfg=60 km。在7维设计空间内对锥导乘波体的气动特性进行代理,其中3个外形参数变量的取值范围为:Macfg=6～20,βcfg=10°～20°,H/W=0.05～0.30。4个飞行参数变量的取值范围为:α=-5°～15°,β=-10°～10°,H=10～100 km,Ma=2～15。由Hammersley试验设计方法给出了7维设计空间中的500个试验点,采用面元法对锥导乘波体进行气动估算,并以此作为训练数据分别对CL,CD,L/D,Cm,Cn,Cl,Xp进行Kriging和LS-SVM代理,共建立了14个代理模型。

2.1 基本外形的气动代理效果

图4～图9为基本外形在不同飞行参数下气动特性的Kriging和LS-SVM代理效果对比。由图可见,首先,Kriging模型的代理效果整体优于LS-SVM模型。这是由于Kriging模型基于插值技术,在训练点处没有代理误差;而LS-SVM模型是基于统计学拟合,并不能保证完全通过训练点,因此Kriging模型对训练数据的利用更加充分。其次,数量级小的模型(如Cn,Cl)的代理效果不如数量级大的模型(如L/D),这是由于数值计算误差对那些数量级小的模型影响更显著。另外,还可以看出,基本外形的最大升阻比出现在α=5°左右,若假设质量是均匀分布的,则基本外形的压心在质心之前,不具有纵向静稳定性;基本外形是个扁平升力体,横航向静稳定性导数很小。

图4 升力系数

图5 升阻比

图6 俯仰力矩系数

图7 偏航力矩系数

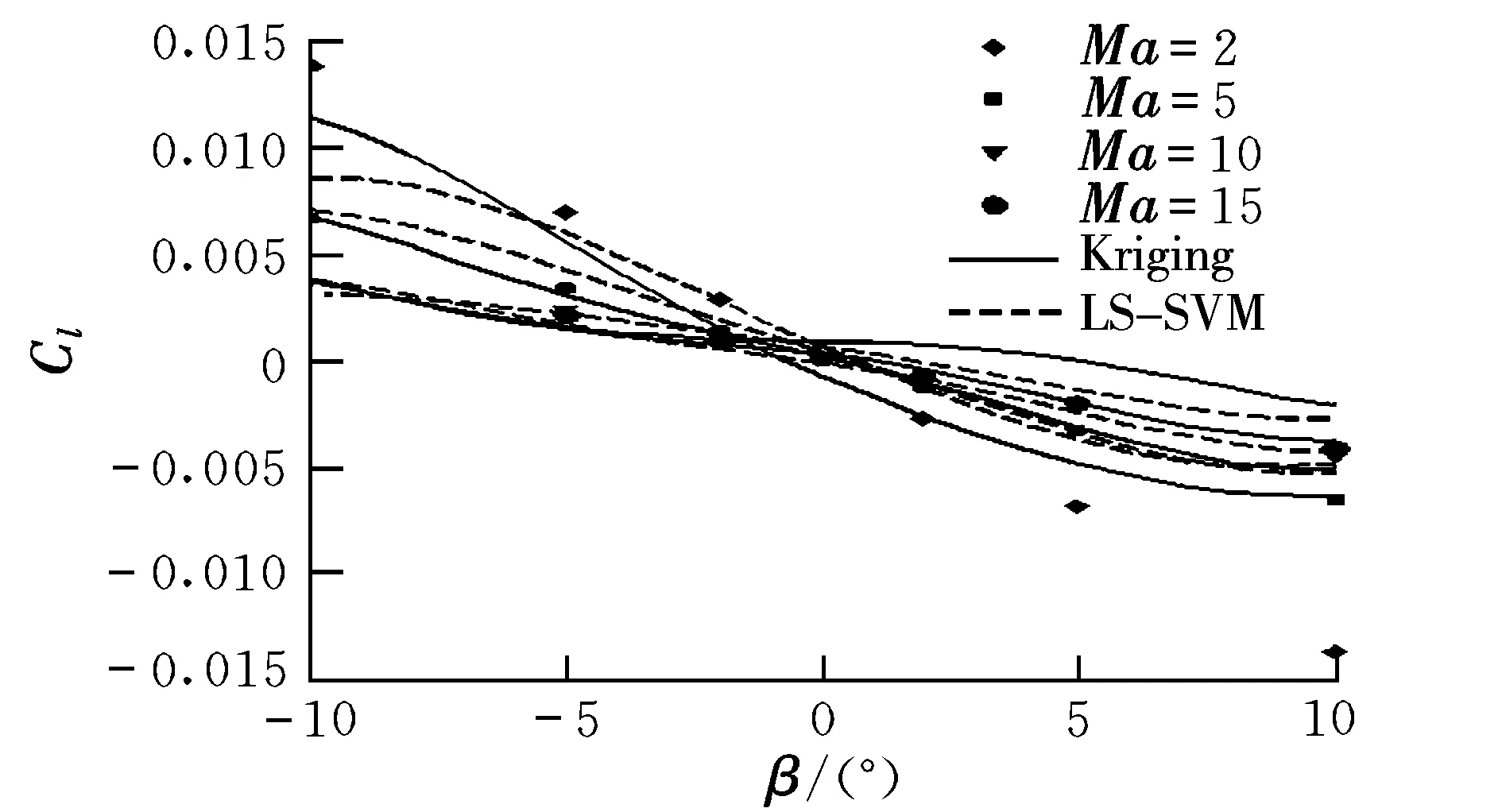
图8 滚转力矩系数

图9 压心超前质心位置

2.2 不同外形的气动代理效果

以各种飞行条件下能出现的最大升阻比为代表,图10～图12为锥导乘波体气动特性随3种外形参数的变化趋势。结果表明,最大升阻比随Macfg变化不大,随βcfg的增大而减小,随H/W的增大而增大。其中由Kriging代理模型得出的最大升阻比与由牛顿面元法估算(设为真实模型)结果符合得很好,而LS-SVM模型由于其本身代理的精度稍差,因而由其分析出的最大升阻比与真实模型存在一定误差。另外,由各图还可看出,锥导乘波体在高超声速飞行时比低超声速飞行时的升阻比更大。

图10 最大升阻比随Macfg的变化

图11 最大升阻比随βcfg的变化

图12 最大升阻比随H/W的变化

2.3 代理建模方法评析

表2为用真实模型和代理模型进行分析生成各图所用机时的对比。表3为两种代理模型的全局代理精度的对比,用相对均方根误差RMSE值进行量化,其定义为:

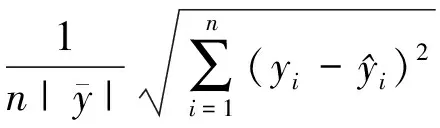
(12)

表2 真实/代理模型用时对比 (s)

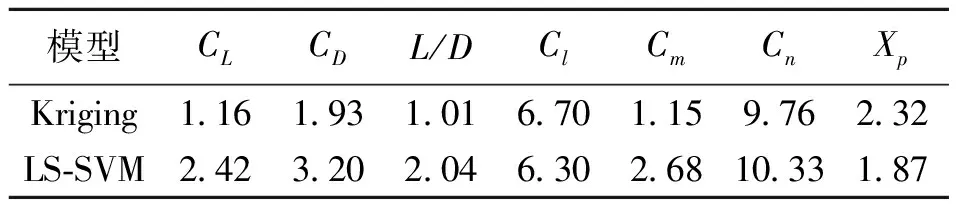
表3 全局代理精度ERMSE对比 (%)

对比结果表明,应用代理模型进行分析的效率显著高于真实模型,对于此高维问题,Kriging模型的代理精度整体优于LS-SVM模型,两种模型对数量级大的模型的代理精度足够高。

3 结束语

本文用Kriging模型和LS-SVM模型对锥导乘波体的气动特性进行了代理,结果表明,Kriging模型能更准确地给出各种条件下的气动特性数据,应用其进行乘波体飞行器初步设计的气动优化的效率将显著提高。整体而言,两种模型对于数量级大的模型的代理精度更高,Kriging模型代理精度比LS-SVM模型更高。适量增加训练点可以提高Kriging模型精度,但LS-SVM模型的代理效果对训练点数的增加并不敏感,对高维问题适应性不好。

[1] 胡乐天,王洪玲,刘洪.基于参数化设计的乘波飞行器概念设计[J].力学季刊,2006,27(3):522-527.

[2] 唐伟,桂业伟.通用大气飞行器的参数化气动布局研究[J].空气动力学学报,2009,27(3):325-328.

[3] 梅东牧,武哲,李天.乘波飞行器的优化设计和气动热计算研究[J].航空计算技术,2008,38(6):13-16.

[4] 杨海江.乘波体气动外形设计与计算[D].南京:南京航空航天大学,2008.

[5] 耿永兵,刘宏,雷麦芳,等.高升阻比乘波构型优化设计[J].力学学报,2006,38(4):540-546.

[6] 车竞,唐硕.类乘波体飞行器的气动力工程计算[J].空气动力学学报,2007,25(3):381-385.

[7] 高建力.高超声速飞行器气动特性估算与分析[D].西安:西北工业大学,2007.

[8] Sacks J,Schiller S B,Welch W J.Design for computer experiments[J].Technometrics,1989,31(1):41-47.

[9] Suykens J A K,Vandewalle J.Least squares support vector machine classifiers [J].Neural Processing Letters,1999,9(3):293-300.

[10] 赵志.乘波构型前体的设计与性能计算[D].西安:西北工业大学,2006.

[11] Naruhisa Takashima.Optimization of waverider-based hypersonic vehicle designs[D].USA:University of Maryland,1997.

Reserchonthesurrogateofmodelaerodynamicperformanceofconederivedwaverider

WANG Shuo, LI Ping, CHEN Wan-chun

(School of Astronautics, BUAA, Beijing 100191, China)

As traditional methods of aerodynamic calculations of waveriders are complicated, inefficient and not accommodated to multi-discipline design optimization, an alternative surrogate is strongly demanded for which it can conquer the contradiction between precision and efficiency of the calculation. Aerodynamic data of the cone derived waverider were collected both at the designed and non-designed points. The calculation was based on Newton panel method. The Kriging and LS-SVM surrogate models were constructed and the performances of surrogating this high-dimensional model were compared. The results showed that Kriging surrogate models were much more valid and it was evidently efficient to pursue optimization works using surrogate models.

cone derived waverider; aerodynamic feature; Kriging; LS-SVM; surrogate model

2011-04-14;

2011-09-07

王烁(1987-)，男，北京人，硕士研究生，研究方向为飞行器多学科设计优化。

V412.4

A

1002-0853(2012)01-0043-05

(编辑：姚妙慧)