基于多准则决策的作战飞机顶层方案优选

赵锁珠, 李军

(西北工业大学 航空学院, 陕西 西安 710072)

基于多准则决策的作战飞机顶层方案优选

赵锁珠, 李军

(西北工业大学 航空学院, 陕西 西安 710072)

提出了综合应用灰色关联投影法、加权求和法、加权求积法和基于理想点决策法来实现对无人作战飞机顶层方案的优选,并着重介绍了多准则决策方法及实施过程。该方法采用不同的公度化方法处理相应的评价指标,对多目标、多层次指标体系进行赋权,利用权重将评价指标联系在一起,并将四种准则决策法进行综合,依据决策者的偏好,最终实现顶层方案的优选。最后,通过制空无人作战飞机顶层方案优选的例子,证实了所提方法是可行且有效的。

无人作战飞机; 多准则决策; 评价指标体系; 方案优选

引言

未来的局部战争将会是高性能的有人驾驶作战飞机、无人作战飞机与高精度武器系统的高度结合。作为战斗机研发的技术储备研究,需要为制空无人作战飞机选择一个切实可行的顶层方案。飞机顶层设计是对飞机设计从顶层的角度出发进行研究,属于概念设计范畴[1],其目的是为初步设计提供一个可行的最佳总体方案,它的设计成果直接影响飞机最终的综合作战效能水平。作战飞机顶层方案优选已成为目前国内外研究的重点和难点,由于设计问题的复杂性和决策方法的局限性,使得在方案评价方面目前还没有一种通用且有效的方法[2-3]。传统的顶层设计方案是在飞行性能、空气动力、重量和推力之间作权衡。随着航空技术和相关技术的不断发展,隐身能力、可靠性、维修性、保障性和可扩展性等也被纳入作战飞机设计的评价指标体系。对作战飞机顶层方案进行评价时,必须要吸收不断发展的新思想、新技术。本文综合应用灰色关联投影法、加权求和法、加权求积法和基于理想点决策法来实现对无人作战飞机顶层方案的优选,决策方法对无人作战飞机的顶层方案选型具有重要的借鉴意义。

1 多准则决策方法

多准则决策法能够对方案作出全局性、整体性的评价,从而对方案进行排序和优选,因此非常适合于方案评价决策层。常用的多准则决策法有加权求和法、加权求积法、灰色关联投影法、基于理想点决策法等[4-6]。

1.1 指标值的公度化处理

针对指标数值范围不一致问题,对各分项能力进行公度化处理,处理后各分项数值都介于0～1之间,使分项能力之间数值匹配,具备一致性,并以此值作为该项指标的指数值。针对不同的评价指标,提出适用的公度化处理方法,主要有线性函数法、凹形函数法、凸形函数法和S形函数法。

线性函数对越大越好的指标:

(1)

对于越小越好的指标,用Amax-Ai作分子。适用指标类型:改善效果随性能线性增加,如载弹能力。

凹形函数对越大越好的指标:

(2)

对于越小越好的指标,用Amax-Ai作分子。适用指标类型:在低端改善效果明显，高端不明显,如机动性能。

凸形函数对越大越好的指标:

(3)

对于越小越好的指标，用Amax-Ai作分子。适用指标类型:低端效果不明显，而高端效果明显,如隐身性能。

S形函数对越大越好的指标:

(4)

对于越小越好的指标，用Amin-Amax作分母。适用指标类型:低端、高端改善效果均不明显,如态势感知能力。

1.2 指标权重及指标值的确定

关于权重的设定方法很多,其中具有代表性的方法有层次分析法、群定权方法、粗糙集法等。层次分析法是一种将定性与定量相结合的有效的评定方法,具体做法是把复杂问题分解成若干层次,每个层次由若干个指标组成;然后以上一层要素为准则,将同一层指标进行两两比较,构造出判断矩阵,确定权向量;解算判断矩阵;判断矩阵通过一致性检验后,得到指标权重[7],设指标权重向量为w=[w1,w2,…,wm]T>0。

将基层的指标值采用加权求和法或加权求积法进行聚合,作为上一层指标的原始数据,逐层向上计算,直至求出顶层指标值。

1.3 多准则决策的计算方法

由于决策方法的差异,导致最终的优选结果不同。本文将加权求和法、加权求积法、灰色关联投影法和理想点决策法进行综合应用,得到多准则决策法的综合法:

Ci=μ1Si+μ2Pi+μ3Gi+μ4Di

(5)

式中,μ为决策偏好因子,根据对决策方法的偏好程度来选取；μ1,μ2分别为加权求和法和加权求积法的因子,这两种方法较为主观,若任一零值指标并不能导致上层指标也为零,则μ1取较大值；若任一指标为零都会引起其上层指标变为零,则μ2取较大值,μ1与μ2之和的取值范围为0.2～0.4；μ3,μ4分别为灰色关联投影法和理想点决策法的因子,灰色关联投影法通过计算备选方案与理想方案的灰色关联度[2],确定方案优劣;理想点决策法通过计算备选方案与理想方案的相对接近度[8],确定方案优劣,这两种方法较为客观,偏好程度相当,故μ3与μ4取值应较为接近,μ3与μ4之和的取值范围为0.6～0.8,并且μ1+μ2+μ3+μ4=1;Si为加权求和值;Pi为加权求积值;Gi为灰色关联投影值;Di为相对接近度。

(6)

式中,wj为指标权重;xj为各分项能力的指标值。

(7)

(8)

式中,rij为其它方案与相对理想方案之间的灰色关联度,其具体的计算可参见文献[2]。

(9)

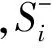
(10)

(11)

2 顶层方案评价指标体系的建立

飞机顶层方案评价指标体系非常庞大和复杂,顶层方案设计阶段可以选取几个对方案有决定性影响的指标。本文以制空无人作战飞机为例,建立其顶层方案评价指标体系[9]。制空无人作战飞机主要进行对空作战,取得制空权,飞行性能无疑是最关键的因素;在未来的空中战场上,以雷达和红外制导的导弹构成了对战斗机的最大威胁,隐身性能也将是关键的因素;由于无人战斗机没有飞行员进行操纵,完全依赖飞行控制系统,操纵性对无人作战飞机来说是一个较为关键的因素。此外,载弹能力、研制风险、可靠性、维修性、保障性、可扩展性等也是较为关键的因素。因此,本文选取飞行性能、操纵能力、隐身能力、载弹能力、研制风险、可靠性、维修性、保障性、可扩展性这9项评价指标为主准则层。主准则层再逐层分解,得到各分准则层。

3 顶层方案的优选

作战飞机顶层方案的优选是飞机研制过程的关键环节,评价指标体系的制订是保证优选结果科学合理的重要基础,不同的评价指标对结果的影响程度不同,因此需要得到评价指标的权重,同时,为消除数值大小对评价结果的影响,需对各指标值进行公度化处理,最终将多准则决策的计算方法与评价体系相结合,对顶层方案进行评价与决策,最终得到满意的方案。

顶层方案的优选过程为:

(1)建立顶层方案评价指标体系;

(2)确定指标体系的权重及指标值;

(3)对各指标值进行公度化处理,消除量纲的影响;

(4)应用多准则决策的计算方法实现对方案的优选。

4 实例分析

4.1 方案及数据处理

某制空无人作战飞机有A,B,C,D,E,F,G,H共8个顶层设计方案,主要设计特点如下:

方案A:小展弦比梯形翼,外倾的“V”型尾翼,两侧进气,宽机身内置武器舱设计。

方案B:中等后掠角的对称菱形翼,外倾的“V”型全动尾翼,背部进气,几乎所有的边缘和折角都沿少数几个方向设计,武器内置。

方案C:常规布局,较大后掠角的小展弦比三角翼,倾斜尾翼,机腹进气。

方案D:常规布局,倾斜双垂尾,全动平尾,两侧进气,无隔道超声速进气道(DSI),推力矢量控制,武器内置。

方案E:箭形翼身融合鸭式布局,全动可收放鸭式前翼,倾斜双垂尾,腹部进气,武器内置。

方案F:无尾布局,“W”形中单翼,大三角形全动鸭式前翼,内翼后缘前掠,外翼后缘与前缘平行,全动鸭翼与机翼平行,武器内置。

方案G:大三角翼隐身飞翼布局,两侧进气,高度翼身融合,宽机身内置武器舱设计。

方案H:鸭式布局,小展弦比中等后掠角三角机翼,近距耦合的全动鸭翼,外倾的“V”型全动尾翼,两侧进气,无隔道超声速进气道(DSI),推力矢量喷口,武器内置。

根据前文建立的指标体系,请10位专家按照两两相对重要性给出每层的评判矩阵,并分别为8个方案的指标打分,得到指标量化值,并进行公度化处理。限于篇幅,表中仅列出主准则层评判矩阵(见表1)和公度化后的各指标值(见表2)。计算得到各个评价指标的权重向量为:

w=[0.19, 0.11, 0.17, 0.15, 0.10, 0.06,0.06, 0.10,0.06]

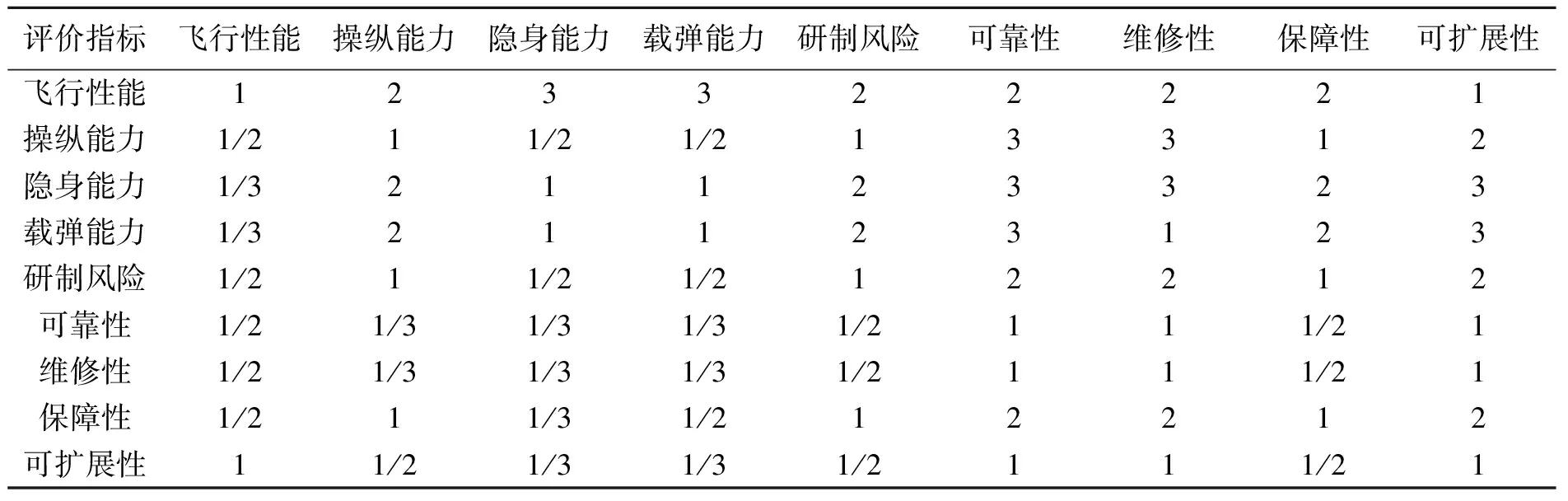
表1 评价指标的判断矩阵

表2 决策指标的规范化数据

4.2 方案优选及结果分析

由式(6)可得加权求和值;由式(7)可得加权求积值;由式(8)可得到各个设计方案的灰色关联投影值;由式(10)和式(11)可得负理想方案为{0.23,0.27,0.25,0.29,0.30,0.29,0.20,0.31},正理想方案为{0.15,0.12,0.19,0.10,0.08,0.09,0.21,0.06};由式(9)可得目标点对于理想点的相对接近度;取μ1,μ2,μ3,μ4分别为0.2,0.2,0.3,0.3,由式(5)可以得到综合评价的决策值。计算结果如表3所示。

表3 多准则决策的计算结果

由表3可知,方案H最优,方案D,E次优,方案A,B,C,F较差,方案G最差。分析表2和表3的结果可知,采用小展弦比中等后掠角的三角机翼、外倾的“V”型全动尾翼、两侧进气、无隔道超声速进气道(DSI)、武器舱内置等特点的设计方案H是一款比较综合的设计方案,该方案较好地权衡了各个主要指标,虽然其单项能力值并不是很突出,但整体结果较优;而采用大三角翼隐身飞翼布局的G方案,虽然隐身性能最优,但其它重要的指标性能较差,导致整体结果最差。可以将A,B,C,G,F方案淘汰掉,对H,D,E方案进行进一步设计,在获取更详细的参数信息后,采用该方法确定出最终的顶层方案。

5 结论

(1)给出了作战飞机顶层方案优选的多准则决策方法,将灰色关联投影法、加权求和法、加权求积法和基于理想点决策法这4种准则决策法有效结合,可以为作战飞机顶层方案优选提供科学的决策,减少决策的盲目性,提高决策效果。

(2)指标体系的赋权及赋值方法和适用于不同评价指标的公度化处理方法,能够全面而准确地反映出各个评价指标的重要度和评价指标的效果。

(3)通过制空无人机顶层方案优选的实例,证实此方法的科学性与可行性。决策方法对作战飞机的顶层方案选型具有重要的借鉴意义。

[1] Mavris D N,Delaurentis D.An integrated approach to military aircraft selection and concept evaluation[R].AIAA-95-3921,1995.

[2] 解建喜.军用飞行器顶层设计决策理论和工程应用研究[D].西安:西北工业大学,2007.

[3] Jilla C D,Miler D W,Sedwick R J.Application of multi disciplinary design optimization techniques to distributed

satellite systems[J].Journal of Spacecraft and Rockets,2000,37(4):481-490.

[4] 黄俊,武哲,孙惠中.作战飞机总体设计评价准则和评价方法研究[J].航空学报,2000,21(1):70-73.

[5] 魏世孝,周献中.多属性决策理论方法及其在C3I系统中的应用[M].北京:国防工业出版社,2001:5-18.

[6] Biltgen P T, Mavris D N. Technique for concept selection using interactive probabilistic multiple attribute decision making [J]. Journal of Aerospace Computing, Information, and Communication, 2009, 6(1):51-67.

[7] 许树柏.层次分析法原理[M].天津:天津大学出版社,1988:25-61.

[8] 李军.现代运输机综合性效评估和软件开发[D].西安:西北工业大学,2010.

[9] 刘晓东.作战飞机总体设计方案评审指标体系研究[J].系统工程与电子技术,2004,26(4):449-453.

Schemeselectionofaircrafttop-layerdesignbasedonmulti-criteriadecision-makingapproach

ZHAO Suo-zhu, LI Jun

(College of Aeronautics, NWPU, Xi’an 710072, China)

In this paper, a multi-criteria decision-making method which combines the grey relation projection method,weighted summation method, weighted product method and ideal point decision making reasonable for unmanned combat aerial vehicle top-layer scheme selection is presented,and how to use the integrated method is introduced. The developed method can deal with evaluation index by different normalized method, to obtain the weights of the evaluation indexes which involve multi-criteria and multi-layers, and the evaluation indices are contacted by the various weights. The best scheme can be found by applying the multi-criteria decision-making approach which combines four multi-criteria decision-making approaches by decision preferences. Finally,the effectiveness and feasibility of the method are validated by using an example of unmanned combat aerial vehicle (UCAV) top-layer scheme selection.

unmanned combat aerial vehicle (UCAV); multi-criteria decision-making;evaluation index system; scheme selection

2011-04-20;

2011-10-09

武器装备探索基金资助(7130629-2)

赵锁珠(1983-),男,陕西渭南人,博士研究生,主要从事飞行器总体设计与作战效能的综合研究。

V221; V279

A

1002-0853(2012)01-0029-05

(编辑：姚妙慧)