小目标识别的小波阈值去噪方法
刘希佳,陈 宇 ,王文生,刘 柱
(长春理工大学 光电工程学院,吉林 长春30022)
1 引 言
在图像的获取和传输过程中,由于一些内在或外在因素的影响,所获得的信息或所传递的信息会受到一定的干扰,不可避免地引入一些噪声,使终端获取的信息失真;当噪声严重时,甚至无法辨认出其中的信息,这时,就需要对含噪图像进行去噪处理。对信号进行去噪处理的方法很多,小波分析作为目前比较前沿的图像处理手段,是一种时频局部化的分析方法。小波分析具有比其他方法更为优越的性质,如低熵性、多分辨性、解相关性和选基自由性,其中多分辨性又被称为“数学显微镜”[1],它能够聚焦到信号的任何细节进行时频域分析,有利于信号的精确处理。因此,小波分析以其具有的众多优越特性,在图像处理领域倍受重视。
小波去噪的常用方法包括模极大值重构滤波去噪法、基于小波变换域系数的相关性去噪法和小波阈值去噪法等。在众多小波去噪方法中,由Stanford 大学的D.L. Donoho 和I. M. Johnstone 等人提出的小波阈值去噪以其算法简单、计算量小、去噪效果好等优点得以广泛应用。
在小波阈值去噪方法中,软、硬阈值法是目前应用较为广泛的阈值去噪方法。但是,由于其本身存在的缺点和不足( 如硬阈值法的阈值函数在阈值处不连续,在图像重构时会出现局部的振荡现象,称为伪吉布斯现象;而软阈值法的阈值函数虽然具有连续性,但是由于处理后的小波系数与真实值之间存在恒定偏差,使重构后的图像会出现严重的模糊,损失了大量重要细节信息) 直接影响了软、硬阈值法的进一步发展。针对软、硬阈值法的缺点和不足,众多学者和专家纷纷提出了相应的改进方法[2-9],并在一定程度上克服了这些问题,使小波阈值法得到了长足的发展。
在进行小目标识别时,由于小目标的边缘信息很少,一般的去噪方法会损失大量的边缘细节信息[10-11],因此,本文结合了双曲线函数、指数函数和对数函数构造了一个新的阈值函数,采用局部方差估计来估算阈值,对小目标进行去噪处理,并利用联合变换相关器对小目标进行了目标识别实验。
2 光学实验原理

图1 联合变换相关器原理图Fig.1 Schematic diagram of joint transform correlator
采用光电混合式联合变换相关器进行了目标识别实验,图1 为联合变换相关器的原理图。此系统采用了氩离子激光器作为光源,经光束衰减器调制输出光强,光束提升器提升光束高度,显微物镜进行聚焦,针孔进行空间滤波,偏振器调节偏振方向,经准直透镜形成准直、扩束的平行光,再经半反半透镜将光束分为两路: 其中一路用于获得联合变换功率谱,即将由CCD1 实时记录的目标图像输入进PC1 中,与事先存储在PC1 中的参考图像一起输入到电寻址液晶EALCD1 中,联合图像经傅里叶变换透镜FTL1 后,由CCD2 进行探测,得到目标图像和参考图像的联合变换功率谱,然后输入到PC2 中显示;另一路用于获得相关点图像,将PC2 中的功率谱输入到EALCD2 中,经傅里叶变换透镜FTL 2 后,由CCD 3 摄取目标图像与参考图像的联合变换相关点,根据相关点的位置,就可以确定目标及其所在位置[1]。
3 小波阈值去噪原理及步骤
3.1 小波阈值去噪原理
对于小波阈值去噪的原理,最常用的就是Donoho 等人在1995 年所提出的小波阈值去噪方法,通过此方法在小波域内对小波系数做相应的处理,最终可获得更多的有用信息。
噪声图像模型:

式中:f(x,y) 为含噪图像信号;s(x,y) 为原始图像信号;n(x,y) 为噪声信号。
因为小波变换是一种线性变换,因此对式(1) 做小波变换,有:

式中:WTf为含噪图像信号f(x,y) 对应的小波系数;WTs为原始图像信号s(x,y) 对应的小波系数;WTn为噪声信号n(x,y) 对应的小波系数。
由于无噪图像在时间或空间上具有连续性,经过小波变换后,在小波域内其系数的模值一般比较大,而且分布在少数位置上。对于噪声来说,其分布是随机的,没有一定的连续性,经过小波变换后,在小波域内其系数的模值一般比较小,且分布比较广。
在小波域内对小波系数进行适当的修改,通过一定的方法和手段去除或降低噪声所对应的小波系数,这样就可获得所需要的信息。
3.2 小波阈值去噪步骤
小波阈值去噪的一般步骤如图2 所示。

图2 小波阈值去噪的一般步骤Fig.2 General steps of wavelet threshold de-noising
其中:f表示含噪图像信号;W表示未经阈值处理的小波系数;W^ 表示经过阈值处理的小波系数;f^表示去噪后的图像信号。
具体操作如下:
(1) 选定小波函数及分解的层数n,对含噪图像信号进行小波变换,得到低频概貌系数( LL) 和高频细节系数:水平系数( LH) 、垂直系数( HL) 和对角系数( HH) ,图3 为3 层小波分解示意图。

图3 小波分解示意图Fig.3 Schematic diagram of wavelet decomposition
(2) 通过阈值和阈值函数对所获得的高频系数进行处理,得到新的小波系数。
对小波系数进行处理的方法通常有硬阈值法和软阈值法,其阈值函数分别为:

软、硬阈值函数如图4 所示。
由于硬阈值函数在阈值处的不连续性,使得重构后的图像会出现局部的抖动现象,使图像产生失真。软阈值法虽然克服了硬阈值法在阈值处不连续的缺点,但是在|W|≥λ 时,W^ 与W之间总是存在恒定偏差,直接影响重构图像与原始图像的接近程度; 当然,即使其恒定偏差为零,去噪效果也未必好。
(3) 对新获得的小波系数进行重构,获得消噪后的图像信号。
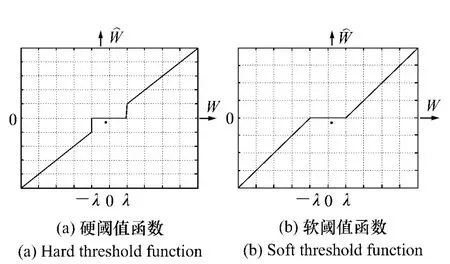
图4 软、硬阈值函数示意图Fig.4 Schematic diagrams of soft and hard thresholds
4 阈值和阈值函数的选取
4.1 阈值的选取
阈值选取的优劣对图像整体噪声的滤除有着非常重要的影响。阈值过小,滤噪效果较差,但是边缘细节信息保留得较好,拟合程度( 与无噪信号的接近程度) 较高; 阈值过大,图像比较平滑( 噪声去除较好) ,但是边缘细节信息损失太多,会使滤噪图像模糊不清而失真。因此,一个好的阈值一定要兼顾平滑和拟合两个方面[4]。

式中:j为分解尺度(j=1,2,…,n) ,n为分解层数;噪声的标准差为:

式中:σj,k表示第j层,第k子带上的标准差,k为高频子带(k=1,2,3;分别表示LH 子带,HL 子带和HH 子带) 。
4.2 阈值函数的选取
(1) 小波系数模值大于阈值
对双曲线函数做适当的改进,并将其作为阈值函数。
双曲线函数的标准方程为:

渐近线方程为:

方程的解为:

当a=b=λ 时,渐近线方程变为:W^ = ±W;方程的解变为:可以看出,此函数是软阈值法的扩展,为了使此函数兼顾硬阈值法的特点,将其进行适当的修改,以获得更好的去噪效果。
当|W|≥λ 时,有:+1 ≤2( 单调递减) ;取对数:≤0( 单调递增) ; 再取指数:≤1( 单调递增) ;为了满足随着|W|的增大,而使得无限接近,故而取:( 单调递减) ;最终,|W|≥λ 时的函数取为:
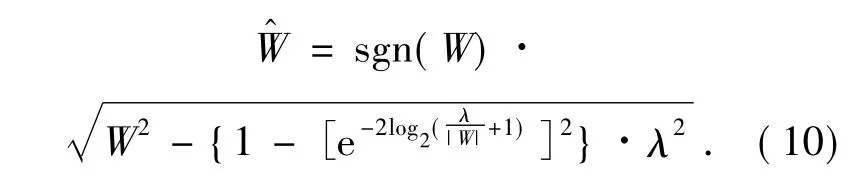
当|W|→∞时,有: | |W^| - |W| |→0,其克服了软阈值具有恒定偏差的缺点,得到了更加精确的小波系数,使得去噪效果更优。
综上,经过修改后的双曲线函数为:
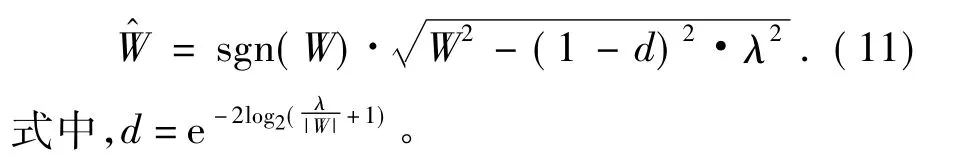
(2) 小波系数模值小于阈值
传统的软、硬阈值法对小波系数中较小的系数大都采取全部置零的方法,这种处理方法将会丢失一些边缘信息,从而使图像边缘模糊,产生失真。针对这一缺点,本文利用指、对数函数的性质,给出了一个函数,用以处理这部分小波系数。此函数克服了对较小的小波系数处理不当的缺点,保留了更多的边缘信息,得到了更高的信噪比。当然,保留更多边缘信息的同时,也会引入一些噪声。但是,对任何一个掺有噪声的信号来说,到目前为止尚无法做到在消除全部噪声的同时,使原信号信息得以完全保留,只能做到在消除噪声的同时,保持较高的信噪比,以获得更多的有用信息。
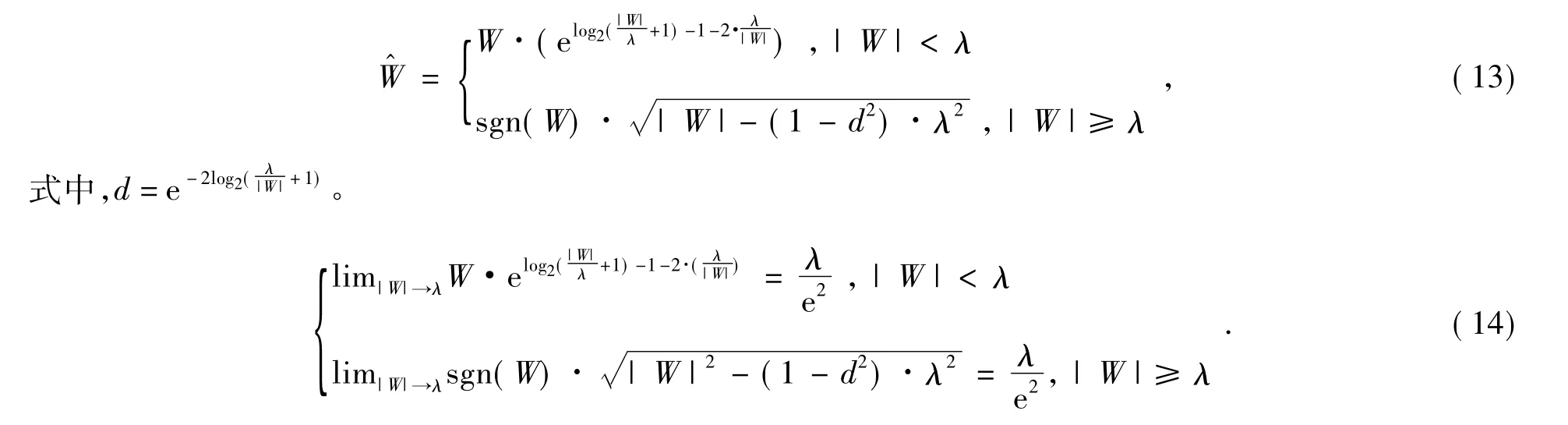
当|W| <λ 时,有:<2( 单调递增) ;取其对数有:-1 <0( 单调递增) ;再取指数有:<1( 单调递增) ;为使函数光滑连续,而且保持函数在阈值处的连续性,则函数最终取为:

对其求导:

综上所述,本文的阈值函数取为:
由上式可见,该阈值函数在阈值处是连续的。
本文改进的双曲线阈值函数如图5 所示。由图5 可见:此阈值函数在阈值处具有连续性,使图像的边缘信息得到了更多的保留,阈值两侧的曲线均为光滑、连续的曲线,分别具有高阶连续的导数。

图5 本文选取的阈值函数Fig.5 Threshold function selected in this paper
4.3 图像信噪比及均方根误差
信噪比( SNR) :
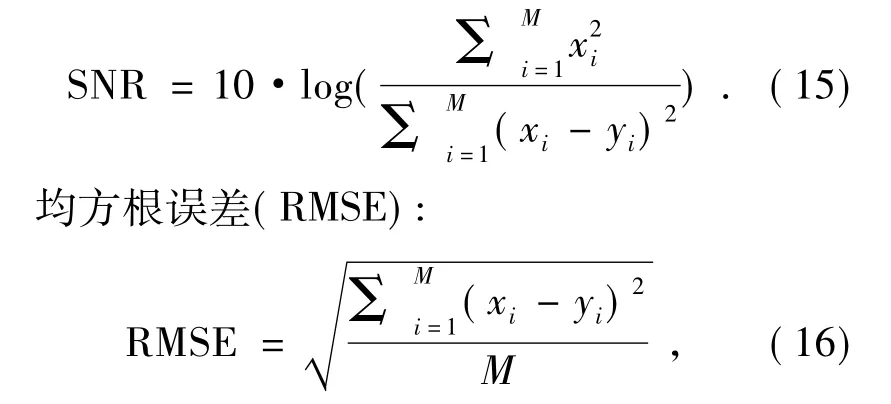
式中,xi(i=1,2,3……M) 为原始图像的第i个像素的灰度值;yi(i=1,2,3……M) 为经阈值处理过的图像的第i个像素的灰度值;M为像素数。SNR 的值越大,表示失真越少; RMSE 的值越小,表示滤噪图像越来越接近无噪图像。
信噪比提高( ISNR) :

其表示滤噪图像相对于噪声图像信噪比的提高量占噪声图像的比例; SNR'是去噪后图像的信噪比;SNR 是噪声图像的信噪比。
5 图像的MATLAB 处理及分析
通过MATLAB 软件进行图像及数据处理,选取高斯噪声作为噪声源进行仿真实验,其噪声均值为0,方差为0.01,图像分辨率为499 ppi ×348 ppi的BMP 格式的文件。从理论上讲,小波滤波器的长度越长,去噪效果应该越好,但计算量也会随之增加,同时造成图像细节的过平滑。因此,本文选取“sym6”作为小波,并对目标图像进行5层小波分解。
对多幅图像进行了滤噪处理,均取得较好的效果。作为实例,选取如图6( a) 所示的以天空为背景的小目标含噪图像进行了分析与研究。以下综述了软、硬阈值法和本文阈值法的去噪实验,分别从视觉效果、信噪比和均方根误差对各阈值法进行了对比,并阐述各种阈值去噪法的优、缺点。

图6 噪声图像及各阈值法去噪后的图像Fig.6 Noise image and de-noised images
从表1 和图6 可以看出: 通过硬阈值法获得的SNR 与RMSE 处于软阈值法和本文阈值法之间,滤噪效果一般,与软阈值法相比获得的边缘信息较多,但由于其阈值函数缺乏连续性,使得重构后的图像出现局部的抖动( 振铃) 现象,损失了较多的图像边缘细节信息,影响了去噪效果。软阈值法对噪声的滤除比较彻底,图像看起来比较平滑;但是,由于软阈值法对较小的小波系数处理不当,使得噪声被滤除的同时,损失了大量的边缘细节信息,使得图像的边缘较为模糊,图像的SNR过低,失真较为严重。

表1 各阈值去噪法的SNR、RMSE 及ISNR(含噪图像的信噪比为:19.4037)Tab.1 SNR,RMSE and ISNR of de-noised image obtained by three de-noising methods(the SNR of noisy image is 19.4037)
从所得数据可以看出,采用本文的阈值函数得到了更高的SNR 和更好的RMSE,滤噪后获得的图像信息较多,SNR 提高的最为明显; 从图像上看,噪声滤除效果很理想,在保留了更多边缘信息的同时,较好地抑制了高斯噪声,并且无明显的振铃效应产生。
6 计算机仿真及光学实验
6.1 计算机仿真实验
利用MATLAB 软件进行了仿真实验,对以图6( a) 为例的小目标图像进行了相关识别研究,选取均值为0,方差为0.01 的噪声源,图像分辨率为499 ppi×348 ppi,采用“sym6”作为小波,进行5 层小波分解。图7 分别为含噪图像和各去噪图像的二维相关峰模拟图及其能量分布图,相关峰值数据是运行MATLAB 程序后,从所生成的数据包中查得的。
图7( a) 是由噪声图像得到的二维相关峰,图中几乎看不到相关点,其能量分布如图7( e) 所示,能量较弱; 图7( b) 为经软阈值去噪处理后得到的二维相关点图像,图7( f) 为其能量分布图,相关峰相对强度为14.355 3,从该图中可以看出,相关峰能量有了一定的增强,但是因其失真较为严重,将相关峰能量淹没其中,使相关点模糊不清,无法辨认;图7( c) 是经硬阈值去噪后得到的二维相关点图像,图7( g) 是其能量分布图,相关峰相对强度为16.823 4,从图中可以看出,相关峰能量得到了一定的增强,但因硬阈值法对噪声滤除的不足,滤噪图像中仍存在一些噪声,使得相关峰的对比度有所降低,从而影响到目标的探测与识别;而经过本文方法处理后的图像,很好地抑制了噪声,保留了大量的边缘信息,从图7( d) 中可以看出相关点的亮度得到了显著的增强,提高了相关探测与识别的能力,其能量分布如图7( h) 所示,相关峰相对强度为17.275 0。因此,无论是从相关峰强度,还是从相关点的亮度对比度来看,本文方法的去噪效果均优于软、硬阈值法。

图7 二维相关峰模拟图及其能量分布图Fig.7 Two dimension correlation peak simulation diagrams and its energy distribution diagrams
由于小目标的有用信息较少,导致其相关峰能量幅值并不很高,但是可以通过后期图像处理有效增强和提取相关峰信息。
6.2 光学实验
利用联合变换相关器对以图6( a) 为例的含噪小目标图像进行了相关识别实验研究,并在功率谱面做了拉普拉斯变换预处理,分别得到了噪声图像和各去噪图像的相关峰图像,如图8所示。
由图8 所示的光学实验结果可以看出,含噪图像中,相关峰被噪声完全淹没,无法实现光学相关识别。用Photoshop 图像处理软件进行由软、硬阈值法和本文方法得到的光学图像中的相关点亮度探测,得到图8( b) 、( c) 和( d) 的相关峰相对亮度分别为43、46 和51。可以看出,本文方法得到的相关峰亮度值最高。另外,从软、硬阈值法得到的相关峰图像中也可以看出,虽然相关点亮度有所提高,但其对比度仍较差,不利于后续处理中相关峰坐标信息的提取。而通过本文去噪法,可有效提高相关峰亮度及相关面的对比度,有利于后续处理中提取相关峰坐标信息,实验效果较好,如图8( d) 所示,从图中可以明显的看出,本文方法得到的相关点亮度明显强于软、硬阈值法得到的相关点亮度,进而从光学实验上说明了本文方法的优越性。

图8 不同处理方法得到的光学相关识别结果Fig.8 Results of optical correlation recognition by different de-noising methods
7 结 论
本文对以海天为背景的小目标图像进行了去噪实验,对阈值函数进行了算法改进,最终得到的信噪比相对于含噪图像提高70.803 8%。计算机仿真实验和光学实验表明:与传统的软、硬阈值法对噪声的滤除作用相比,本文所提出的阈值函数法去噪效果更优,识别能力较好,表明了该方法在小目标图像处理领域具有一定的实用性。
[1] 陈宇,王文生,苗华,等.灰度变换在光学相关探测与识别中的应用[J].仪器仪表学报,2005,26(8) :676-677.CHEN Y,WANG W SH,MIAO H,et al.. Application of gray-scale transformation in optical correlation detection and recognition[J].Chinese J. Scientific Instrument,2005,26(8) :676-677.( in Chinese)
[2] 李祥兵,肖合林.基于Matlab 的小波阈值折中去噪算法研究[J].电脑开发与应用,2009,22(6) :428-430.LI X B,XIAO H L. Research on wavelet threshold compromise denoising method based on matlab[J].Computer Development Appl.,2009,22(6) :428-430.( in Chinese)
[3] 李树玉.改进的小波阈值去噪方法及其在MATLAB 中的仿真[J].噪声与振动控制,2010(2) :121-124.LI SH Y. Improved wavelet threshold denoising method and its simulation using MATLAB[J].Noise and Vibration Control,2010(2) :121-124.( in Chinese)
[4] 孙俊喜,陈亚珠.一种具有边缘保持特性的超声图像小波域阈值去噪新方法[J].光学 精密工程,2002,10(5) :429-433.SUN J X,CHEN Y ZH. Novel speckle reduction for medical ultrasound images based on edge preservation[J].Opt. Precision Eng.,2002,10(5) :429-433.
[5] 苑津莎,张东雪,李中.基于改进阈值法的小波去噪算法研究[J].华北电力大学学报,2010,37(5) :92-96.YUAN J SH,ZHANG D X,LI ZH. Wavelet denoising algorithm based on improved thresholding method[J].J. North China Electric Power University,2010,37(5) :92-96.( in Chinese)
[6] 邓义君,严高师.一种基于小波变换的红外小目标去噪算法[J].强激光与粒子束,2007,19(3) :399-402.DENG Y J,YANG G SH. De-noising algorithm of infrared small target based on wavelet transforms[J].High Power Laser and Particle Beams,2007,19(3) :399-402.( in Chinese)
[7] 王佐成,刘晓冬,薛丽霞.双曲线函数在灰度图像小波阈值去噪中的应用[J]. 计算机工程与应用,2010,46( 35) :177-179.WANG Z CH,LIU X D,XUE L X. Application of hyperbolic function in gray image wavelet threshold denoising method[J].Computer Eng. Appl.,2010,46(35) :177-179.( in Chinese)
[8] 蒋晓玲,高尚兵,曾山佰.一种基于小波变换的图像去噪算法与实现[J].电脑知识与技术,2008,3(8) :1768-1769,1775.JIANG X L,GAO SH B,ZENG SH B. One image denoising algorithm and its implementaion based on wavelet transform[J].Computer Knowledge Technology,2008,3(8) :1767-1768,1775.( in Chinese)
[9] 张维强,宋国乡.基于一种新的阈值函数的小波域信号去噪[J]. 西安电子科技大学学报( 自然科学版) ,2004,31(2) : 296-303.ZHANG W Q,SONG G X. Signal de-noising in wavelet domain based on a new kind of thresholding function[J].J. Xidian University( Natural Science Edition) ,2004,31(2) :296-303.( in Chinese)
[10] 刘伟宁.基于小波域扩散滤波的弱小目标检测[J].中国光学,2011,4(5) :503-508.LIU W N. Dim target detection based on wavelet field diffusion filter[J].Chinese Optics,2011,4(5) :503-508.( in Chinese)
[11] 董宇星,刘伟宁.基于灰度特性的海天背景小目标检测[J].中国光学与应用光学,2010,3(3) :252-256.DONG Y X,LIU W N. Detection of sea-sky line in compocated background based on grey characteristics[J].Chinese J.Opt. Appl. Opt.,2010,3(3) :252-256.( in Chinese)
[12] 唐世伟,林君.小波变换与中值滤波相结合图像去噪方法[J].哈尔滨工业大学学报,2008,40(8) :1334-1336.TANG SH W,LIN J. Image denoising with combination of wavelet transform and median filtering[J].J. Harbin Institute Technology,2008,40(2) :1334-1336.( in Chinese)

