应用模糊数学综合判定饱和砂土地震液化的研究

黎运棻

（水利部山西水利水电勘测设计研究院 山西太原 030002）

实践表明，影响饱和砂土地震液化是多个因素的综合，即使发生液化，随着各因素指标的隶属函数不同，其液化程度也表现各异。即是说，尽管其中某因素的影响有所明确，但综合表现却有一定模糊性，据此可用模糊数学进行综合判定【1】。

1 液化因素集与液化势模糊集

影响饱和砂土地震液化的因素可写成

式中，u1，…，un因素对论域 U的关系为ui∈U；根据现行规范[2]，取 n=7，即 ui包括 7项因素，分别为，为便于表示，本文写成g，h，S，N，d，β，ρ，于是（1）式表示为

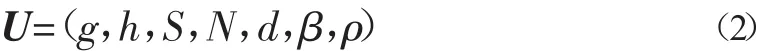
即，（g，h，S，N，d，β，ρ）∈U，式中g为设计基本地震加速度，m/s2；h为地面覆盖的非液化黏性土厚度，m；S为标贯点深度，m；N为自由落锤标准贯入击数基准值，击；d为地面以下地下水位埋深，m；β为调整系数，设计地震第一组取0.8，第二组取0.95，第三组取1.05；ρ为黏粒含量百分率，当小于3或为砂土时，应采用3。各因素指标对液化势的影响不同，如N=30击，可属不液化；N=2击，可属液化。各因素可综合构成4种状况液化势模糊集：即不液化、可能液化、很可能液化、液化，写成

在张弘的论文“饱和砂土液化的模糊综合评判方法”（中国力学学会岩土力学专业委员会论文集，1989.12：258-262）中，曾给出五组隶属函数分布图。本文作者根据上述因素，去掉一组图形，修改了两组图形，增加了g，β，ρ三组图形，并由试点法得出上述7项因素的隶属函数分布图于图1中。图中k=2和k=3的函数呈梯形分布，k=1和k=4的函数图形呈半梯形分布；横坐标为各因素的指标值，均由6个分界点构成模糊交叉；纵坐标分别为函数值，以rivk表示，其中第一个脚标i表示各因素，即i=g，…，ρ，第二个脚标表示液化势v1，…，v4。当某个因素的指标不在图1中的2个或3个液化势范围内时，则相应液化势范围的函数值为0；当因素指标在1个或2个液化势范围内时，表明该因素指标与对应的液化势有关系，则由函数图形确定函数值；函数值在0～1间分布，详见图1。

2 模糊矩阵

设R为论域U中各因素与液化势之间的一个模糊关系，它确定了一个模糊映射，构成一个模糊矩阵，如第j土层的矩阵为：

式中，Rj为第 j土层的模糊矩阵；j=1，2，…，m，则有m个矩阵；rivk为矩阵中的子元素，即隶属函数值，元素中第一个脚标i为论域中的因素，以行排列，第二个脚标vk为液化势，以v1，…，v4从左至右按列排列。

图1 隶属函数图

3 各因素的权重向量

各因素对地震液化的影响程度不同，可以其权重表示，大量震后地面表现显示，N值影响最明显，列为权重首位，作者据21个场地资料分析，由试点法得各因素的权重向量大致为

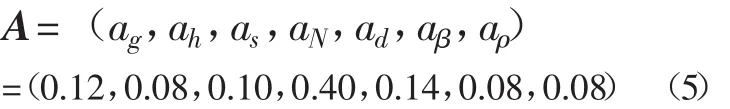
4 综合评判

综合评判是各因素与液化势之间的一个模糊关系，首先给出各土层评判指标，如对土层的评判指标为：

对上式进行归一化处理得

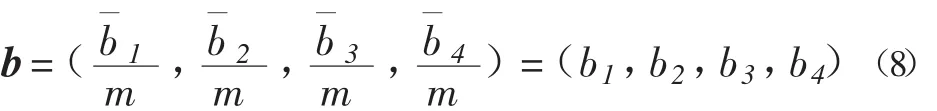
当各土层划分厚度不等或相差较大时，（6）式中最后一个等号右边4项液化势指标需乘以各土层的厚度权重比

并由（7）式得B值，不须归一化，即B=b。式（9）中，Dj为不计非液化覆盖土层的从上至下第j土层厚度，m，其余各项符号同前。

作者据上述方法，对设防烈度7、8度的21个场地，15m深范围内饱和砂土地基分析，给出综合判定液化等级图（图2）。图中，纵坐标为评判指标，以b2-4表示；横坐标为液化指标，以表示。据现行规范0＜ILE≤6，为轻微液化；18，为中等液化；，为严重液化。图中与有较好的相关性（利用指数函数进行相关，相关系数R=0.968）。

作者考虑到液化等级的地面表现会有过渡现象，不宜截然以某一个值来把相连的两个等级划分，从而提出如图中阴影所示的模糊过渡区，得到等级划分如下及图2所示：

图2 b2-4～ILE关系及综合判定图

0.39 ≤b2-4≤0.52,属轻微液化;

0.52 ＜b2-4≤0.53，属轻微～中等过渡；

0.53 ＜b2-4≤0.60，属中等液化；

0.60 ＜b2-4≤0.61，属中等～严重过渡；

0.61 ＜b2-4，属严重液化。

5 工程实例

某场地地面以下0～4m为非液化土层，4～14m为饱和粉细砂层，对该场地进行液化评判。由测试得地基的因素集如左下所示：

得b1=0.3666，b2-4=0.6334，属严重液化。

在国家标准GB50011-2010中【2】，对地面以下15m深度范围内，给出液化判别标准贯入击数临界值公式,按本文符号写成下式:

同时给出划分液化等级的液化指标

以上两式中，Ncr、No为液化判别标准贯入击数临界值和基准值；ILE为液化指数；n为标贯点总数；Ni、Ncri分别为点标准贯入击数的实测值和临界值，实测值大于临界值时，应取临界值的数值；Di为i点所代表土层厚度,上界不高于地下水位；Wi为i土层单位土层厚度的层位影响权函数值，若判别深度为15m，当该层中点深度不大于5m时取10，等于20m时取零值；其余符号同前。如图2所示，当ILE=0，属不液化；0＜ILE≤6，属轻微液化；6＜ILE≤18，属中度液化；ILE＞18，属严重液化 。

由（10）、(11)两式算得 ILE=24.62，属严重液化,两种方法判定一致。

6 结语

本文试用模糊数学理论，建立液化因素集与其液化势的模糊关系矩阵，确定了它的模糊映射，通过权重向量，得到映射的像，即评判指标。经21项场地计算判定，与现行设计规范采用概率方法得到的判定符合，为用模糊数学分析饱和砂土液化奠定了可能性。但由于影响砂土液化的因素很多，且有显著的不确定性，作者收集资料也有限，对各因素的液化势及其向量权重分配，还待更多场地资料进一步研究发展。

[1]汪培庄，韩立岩．应用模糊数学[M]．北京:北京经济学院出版社，1989：160-170

[2]中华人民共和国住房和城乡建设部．GB50011-2010建筑抗震设计计规范[S]．北京：中国建筑工业出版社，2010：23-25