线性离散系统的非脆弱混合H2／H∞动态输出反馈控制

关 威，高斌斌

（沈阳航空航天大学 自动化学院，辽宁 沈阳 110136）

通过鲁棒控制设计技术得到的控制器将会对控制器参数的摄动及不确定性表现出较强的敏感性及脆弱性［1］.这意味着在控制器设计过程中，微小的控制器参数摄动都有可能导致闭环系统性能下降甚至导致系统崩溃.目前，有大量的文章考虑到非脆弱控制及滤波器设计问题［2-7］.然而，已有文献主要考虑单一性能下的控制器设计问题［5-7］.而在考虑混合性能的情况下进行非脆弱动态输出反馈控制器的设计是一个极为复杂而困难的问题.

混合H2／H∞控制器设计技术因其具有H2最优控制及H∞鲁棒控制两者的共同优点，可广泛应用于实际控制工程领域.针对线性系统，混合H2／H∞控制问题已经得到广泛的研究［8-9］.然而，满足混合性能的非脆弱控制器设计方面的成果却很少［10］.文献［10］针对一类线性周期采样系统考虑了稳态协方差及鲁棒H∞性能的非脆弱一致性问题，其中，周期采样系统以间隔的形式进行描述.然而，非脆弱混合H2／H∞动态输出反馈控制器设计问题仍有待解决.基于这一原因，本文在考虑乘性控制器参数变化的情况下，通过线性矩阵不等式方法设计了混合H2／H∞动态输出反馈控制器，从而保证了闭环系统具有渐近稳定性及混合H2／H∞性能.另外，针对凸多面体结构的不确定线性系统，其结果可被推广到鲁棒非脆弱混合H2／H∞控制器的设计中.由于文中所给的设计条件含有等式约束，因此，本文考虑采用文献［11］所提的连续线性规划矩阵方法（SLPMM，Sequential Linear Programming Matrix Method）来解决该非凸的问题，并通过Matlab YALMIP工具包求解.本文涉及的定义及符号如下：P＝PT＞0（P＝PT≥0）说明P为正定（半正定）矩阵；diag｛ρ1，ρ2，…，ρn｝代表对角矩阵，其对角线元素为ρ1，ρ2，…，ρn.另外，本文通过“＊”标注对称矩阵中省略的部分.

1 问题描述

考虑如下离散时间系统：

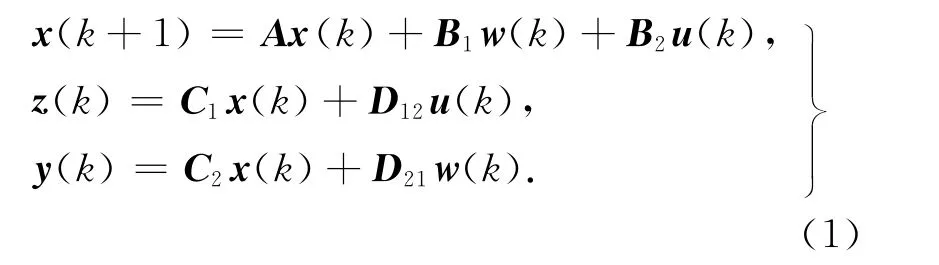
式中，x（k）∈Rn，u（k）∈Rm，w（k）∈Rγ，z（k）∈Rq及y（k）∈Rp分别为系统的状态向量、控制输入向量、扰动向量、控制输出向量及测量输出向量，且假设w（k）为高斯白噪声信号；系统矩阵A，B1，C1，B2，C2，D12及D21为具有相应维数的已知常数矩阵.

本文旨在设计动态输出反馈控制器，其结构描述如下：

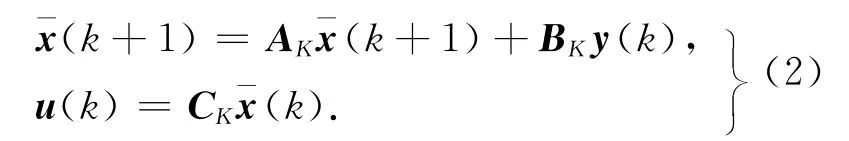
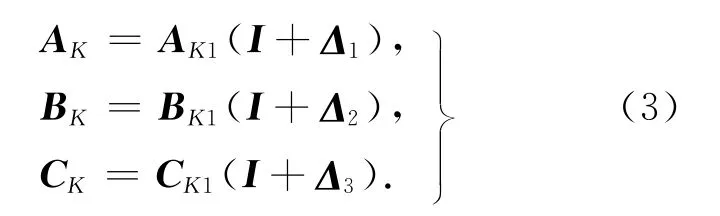
式中，AK1，BK1及CK1为所要设计的控制器参数；Δ1，Δ2及Δ3为控制器增益的变化量，定义如下：

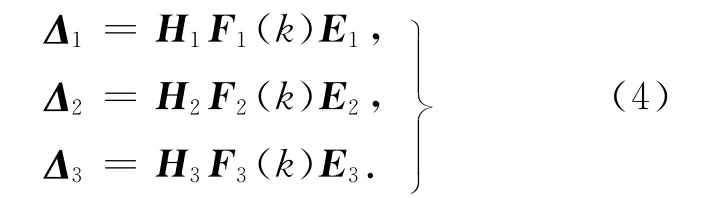
式中，Fl（k）（l＝1，2，3）为实不确定矩阵，且

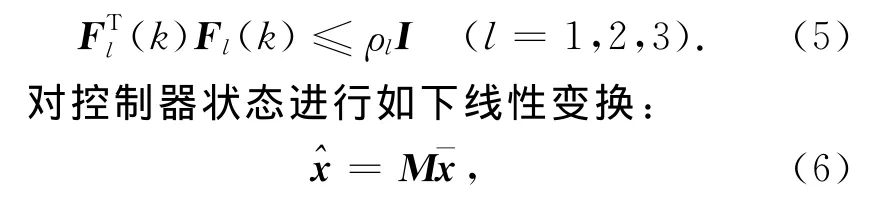
于是可得如下新形式的控制器描述：

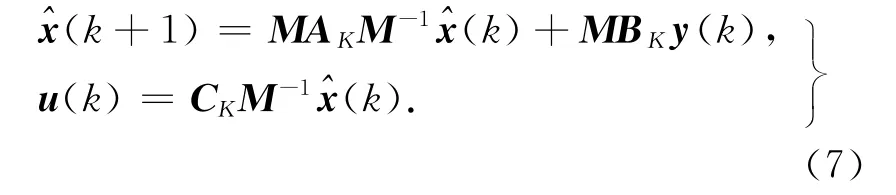
式中，M为可逆矩阵.

将控制器（7）应用于系统（1）中，可得如下闭环系统：

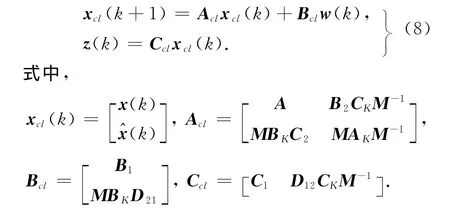
于是，非脆弱混合H2／H∞动态输出反馈控制器设计问题可表述如下：

（1）如不存在外部扰动，即w（k）＝0，那么闭环系统（8）是渐近稳定的；

（2）闭环系统（8）具有 H2／H∞性能，当且仅当传递函数矩阵T（z）＝Ccl（zI-Acl）-1Bcl同时满足‖T（z）‖∞＜γ∞及‖T（z）‖2＜γ2.

以下引理将对本文的主要结论起到支撑作用.

引理1［12］令N＝NT.H及E为具有相应维数的实数矩阵，F（k）满足FT（k）F（k）≤ρI，于是有

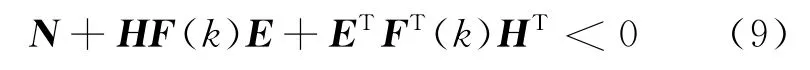
当且仅当存在ε＞0且满足

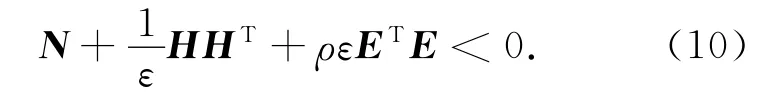
下面给出H2及H∞范数有界的实有界引理.

引理2（H∞范数界）［13］令γ∞＞0，于是可得如下两个等价的条件：

（1）系统（8）为渐近稳定的，且T（z）的H∞范数不会超过γ∞＞0，即

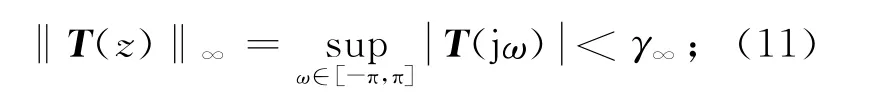
（2）存在一个实数矩阵G∞及对称正定矩阵P∞＝＞0，满足

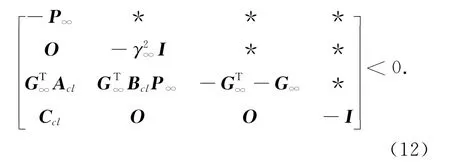
引理3（H2范数界）［14］给定γ2＞0，于是可得如下两个等价的条件：

（1）系统（8）为渐近稳定的，且T（z）的H2范数不会超过γ2＞0，即

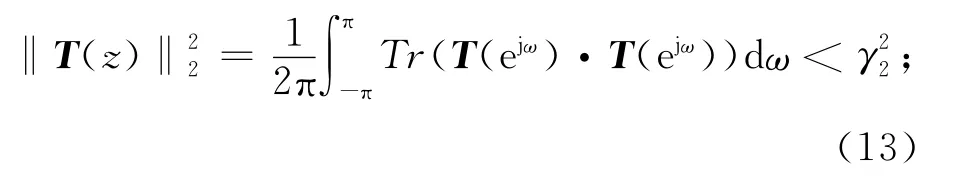
（2）存在矩阵G2、正定对称矩阵P2＝＞0及W＝WT＞0，满足

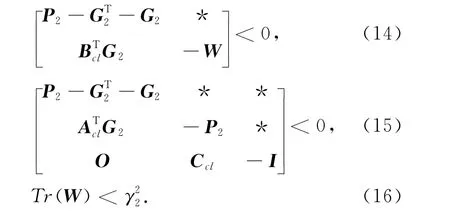
2 主要结果

下面针对控制器不确定的情况给出基于线性矩阵不等式的动态输出反馈混合H2／H∞控制器设计方法.对于所有可容许的乘性控制器增益不确定性，该方法能够保证闭环系统是渐近稳定的且同时满足H2／H∞性能.对于多目标控制问题，通常是给定其中的一个性能指标，然后优化另一个性能指标，或者通过加权实现两者的综合优化.本文采用后者，较好地解决了H2性能和H∞性能之间的综合优化问题 .通过以上分析，混合H2／H∞控制问题可通过求解如下最优化问题解决：

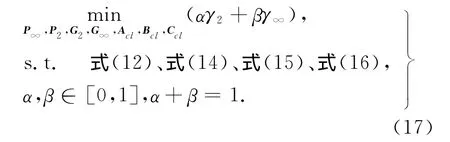
其中，α及β分别为两目标函数的加权系数 .然而，多目标控制问题（17）的求解过程是非凸的并且是难以得到解决的［15］.因此，为了解决上述困难，引入约束G2＝G∞＝G且P2＝P∞＝P.值得一提的是，以上策略被大量用于混合H2／H∞.下面，基于矩阵不等式方法，给出动态输出反馈非脆弱混合H2／H∞控制器存在的充分性条件.首先，给出如下定义：

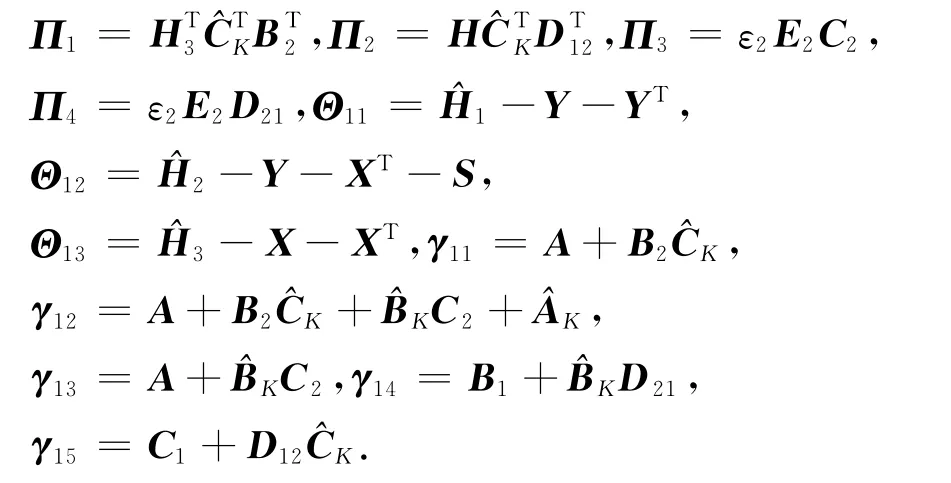
定理 给定标量γ2＞0，γ∞＞0以及加权系数α、β（其中，α、β∈ ［0，1 ］且α＋β＝1），如果存在常数εl（l＝1，2，3）及矩阵

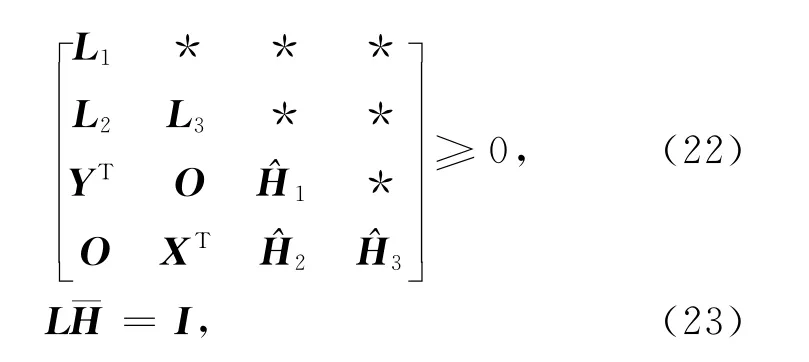
那么，系统（8）是渐近稳定的且满足H2／H∞范数约束（11）和（13）.另外，如果这些不等式存在解，那么控制器可由如下式子给出：

证明 由Schur补引理可得，矩阵不等式（20）及式（21）等价于

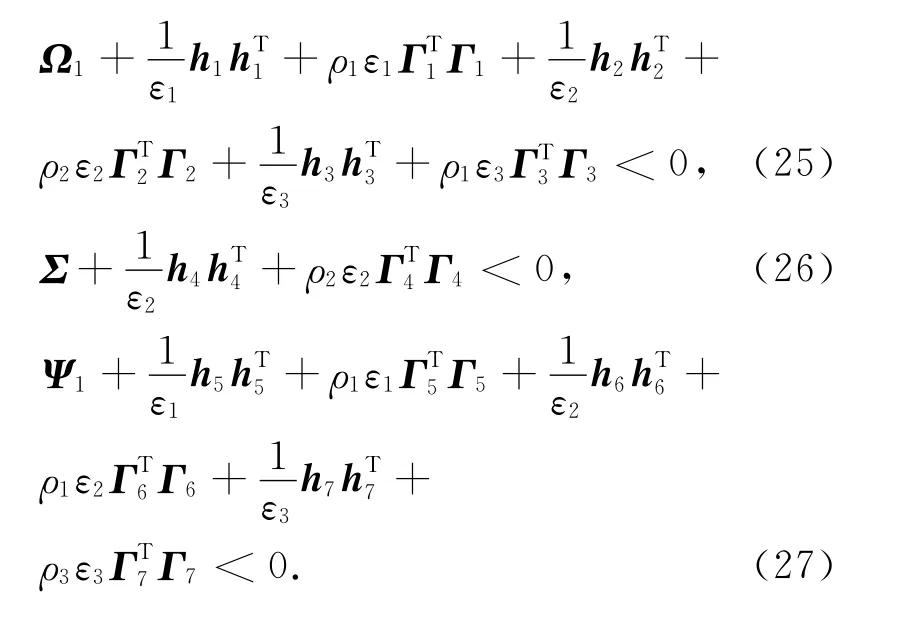
将引理1应用于式（25）、式（26）及式（27），并将式（3）代入可得

构造如下矩阵：

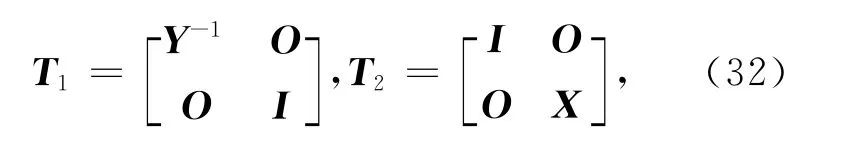
将式（23）代入式（22），并由Schur补引理可得

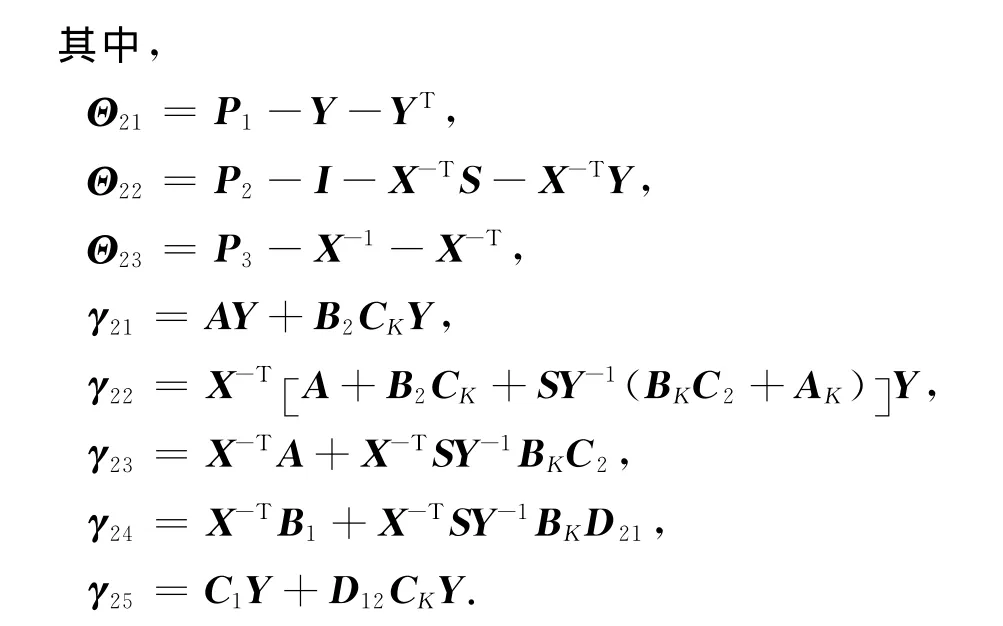
如果定理存在解，那么由式（24）可得矩阵S是非奇异的.定义

其中，U和V是非奇异的 .将式（41）代入式（38）、式（39）及式（40）中，并令M＝VY-1≠O，则有

在式（42）、式（43）及式（44）两边分别同时乘以

因此，由式（17）可得闭环系统（8）是渐近稳定的，且同时满足 H2／H∞范数约束（13）及式（11）.

注：如果对于L＞0和ˉH＞0，不等式

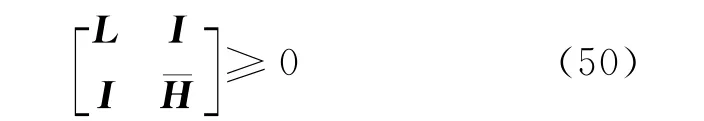
3 仿真例子

3.1 针对确定系统的数值算例

考虑如下系统参数及控制器的增益变化参数：

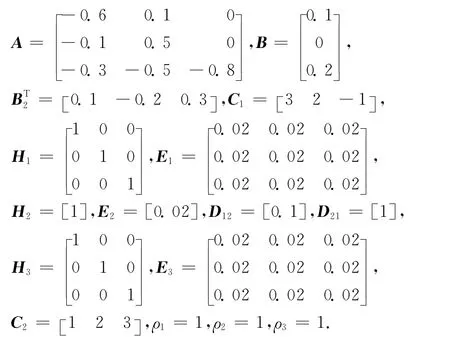
通过带有SeDuMi求解器的YALMIP工具包，求解满足条件Ω＜0、式（22）及式（50）的可行性问题，可得最优H∞性能指标为γ∞＝0.537 5，控制器参数为

另外，在满足条件（19）、Ψ＜0、式（21）、式（22）及式（50）下，可得最小值Tr（W）＝0.348 3，并有

考虑多目标优化问题时，首先设加权系数为α＝0.8，β＝0.2.在约束条件式（19）～式（22）及式（50）下，可得优化指标为0.516 6.控制器参数为

3.2 针对不确定系统的数值算例

考虑如下系统参数：

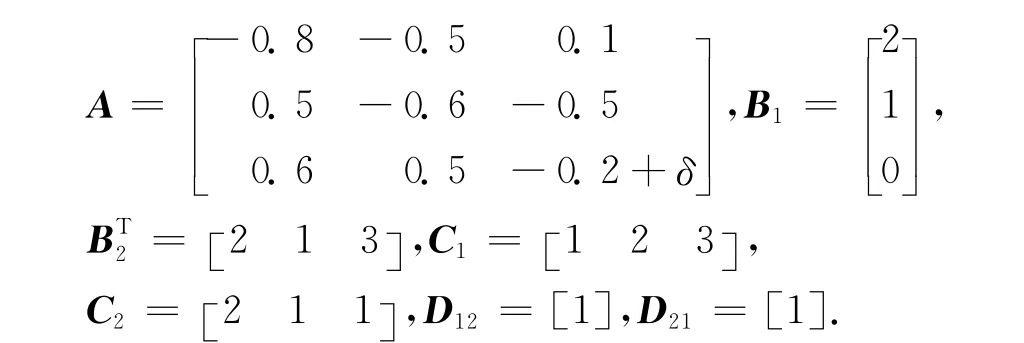
同时，通过最小化指标Tr（W）＝1.681 6可得H2控制器，其控制器参数如下：

进而考虑多目标优化问题，首先设加权系数为α＝0.8，β＝0.2，可得最优性能指标为2.103 1及如下多目标控制器参数：

4 结 语

针对控制器带有乘性变增益情况的离散系统，本文考虑了非脆弱混合H2／H∞输出反馈控制器的设计问题.基于矩阵不等式技术，针对动态输出反馈控制器的存在性给出了充分条件.以所得结果为基础，针对带有凸多面体结构的不确定离散系统，考虑了鲁棒非脆弱混合H2／H∞输出反馈控制器设计问题.

［1］ Bamieh B，Paganini F，Dahleh M A.Distributed control of spatially invariant systems［J］.IEEE Transactions on Automatic Control，2002，47（7）：1091-1107.

［2］ Keel L H，Bhattacharyya S P.Robust，fragile，or optimal［J］.IEEE Transaction on Automatic Control，1997，42（8）：1098-1105.

［3］ Guo X G，Yang G H.Non-fragile H∞filter design for Delta operator formulated systems with circular region pole constraints：an LMI optimization approach［J］.Acta.Automatica Sinica，2009，35（9）：1209-1215.

［4］ Yang G H，Che W W.Non-fragile H∞filter design for linear continuous-time systems［J］.Automatica，2008，44（11）：2849-2856.

［5］ Ding D W，Li X L，Yin Y X，et al.Non-fragile H∞and H2filter designs for continuous-time linear systems based on randomized algorithms［J］.IEEE Transactions on Industrial Electronics，2012，59（11）：4433-4442.

［6］ Yang G H，Wang J L.Non-fragile H∞control for linear systems with multiplicative controller gain variations［J］.Automatica，2001，37（5）：727-737.

［7］ Wang W，Guo X G，Yang F W，et al.H2control for discrete-time system with multiplicative controller gain variations［C］∥Proceeding of the 2nd International Conference on Innovative Computing，Information and Control.Washington D C，2007：592-595.

［8］ Chang X H，Yang G H.Nonfragile H∞filtering of continuoustime fuzzy systems［J］.IEEE Transactions on Signal Processing，2011，59（4）：1528-1538.

［9］ Goncalves E N，Palhares R M，Takahashi R H C.Improved optimization approach to the robust H2／H∞control problem for linear systems［J］.IEEE Proceedings on Control Theory and Applications，2005，152（2）：171-176.

［10］ de Oliveira M C，Bernussou J，Geromel J C.Extended H2and H∞norm characterizations and controller parametrizations for discrete-time systems ［J］.International Journal of Control，2002，75（9）：666-679.

［11］ Zang W L，Wang Y G，Guo Z.Non-fragile consistency control of H∞indices for a class of linear periodic systems［C］∥Proceeding of the 6th World Congress on Intelligent Control and Automation.Dalian，2006：738-742.

［12］ Leibfritz F. An LMI-based algorithm for designing suboptimal static H2／H∞output feedback controllers［J］.SIAM Journal on Control and Optimization，2001，57（6）：1711-1735.

［13］ Xie L，Fu M，de Souza C E.H∞control and quadratic stabilization of systems with parameter uncertainty via output feedback［J］.IEEE Transactions on Automation Control，1992，37（8）：1253-1256.

［14］ Shim D H，Lee H S，Guo L.Mixed-objective optimization of a track-following controller using linear matrix inequalities ［J］. IEEE／ASME Transactions on Mechatronics，2004，9（4）：636-643.

［15］ Gao H J，Lam J，Xie L H，et al.New approach to mixed H2／H∞filtering for polytopic discrete-time systems［J］.IEEE Transactions on Signal Processing，2005，53（8）：3183-3192.