石墨炉原子吸收法检验猪肝中铅回收率不确定度的评估
占永革,龚 剑,黄湘燕
(1.广州大学环境检测中心,广东 广州 510006;2.中山市供水有限公司水质检测中心,广东 中山 528403)
石墨炉原子吸收法检验猪肝中铅回收率不确定度的评估
占永革1,龚 剑1,黄湘燕2
(1.广州大学环境检测中心,广东 广州 510006;2.中山市供水有限公司水质检测中心,广东 中山 528403)
以加标回收实验实际过程及其计算模型为依据,评估石墨炉原子吸收法检验猪肝标准样品中铅含量平均回收率的总不确定度。结果显示,平均回收率的重复性不确定度只占其总不确定度的16%;标准储备液的不确定度只占加标稀释过程总不确定度的38%,是平均回收率总不确定度的0.5%;而加标量观测值的不确定度是平均回收率总不确定度的主要分量,占81%,主要来源于曲线拟合浓度的不确定度。以实际过程及其计算模型为依据的回收率不确定度的评估结果具有更高的严密性和针对性。
化学检测;食品检验;方法偏差;回收率;不确定度
食品检验系符合性检验,当测试结果处于规定指标临界值附近时,测量不确定度对判断结果符合性会产生影响[1],因而合理评估测量不确定度对食品安全检验机构具有重要意义。
食品检验常有较复杂的样品处理过程而给检验结果带来偏差。规范[1]虽给出了不同含量的回收率所允许的参考范围,但并未要求对范围内的非100%回收进行校正,方法偏差便转化为测量不确定度,常成为测量不确定度的主要分量而日益受到重视。
方法偏差及其不确定度的度量常采用标准样品回收法或样品加标回收法。文献[2-12]中常见将平均回收率的重复性不确定度作为其总不确定度,或者将标准物质证书给的不确定度与平均回收率重复性的不确定度进行合成后的结果作为平均回收率总不确定度的处理方法,较少与回收实验过程及其计算模型相联系。本实验尝试以加标回收实验的实际过程及其计算模型为依据的角度,评估石墨炉原子吸收法检验猪肝标样中铅含量的方法偏差的不确定度,获得更严密和更有针对性的评估结果,提高符合性判断的可靠性,对同行测定具有一定的参考作用。
1 材料与方法
1.1 材料与试剂
实验样品为猪肝成分分析标准样品(GBW08551,Pb含量X=(0.54±0.04)mg/kg,k=2);Pb校准液和加标液均由Pb标准物质(GBW(E)080129,Pb质量浓度100.0μg/mL,U=0.8%,k=2)配制;消解用硝酸、高氯酸等试剂均为分析纯;实验用水均为超纯水。
1.2 仪器与设备
ICE3500原子吸收光谱仪 美国Thermo公司;BT124S 120g/0.1mg电子天平 德国Sartorius公司;PH-30D陶瓷涂层精密温控电热板 韩国Daihan Scientific公司。
1.3 校准曲线及其溶液配制
吸取V移1=1.00mL Pb质量浓度为100.0μg/mL的标准储备液cs0,用0.5mol/L硝酸定容于V容1=100mL容量瓶中,得含Pb质量浓度值cs1=1000ng/mL的标准使用液。
分别吸取标准使用液0.00、1.00、2.00、4.00、6.00、8.00mL于6个100mL容量瓶中,用0.5mol/L硝酸定容,得Pb含量0、10、20、40、60、80ng/mL的校准溶液系列。
所用吸量管为A级硼硅玻璃,容量瓶为A级钠钙玻璃。配制校准溶液时的平均水温15℃,上机时的18℃。Pb校准曲线数据见表1。
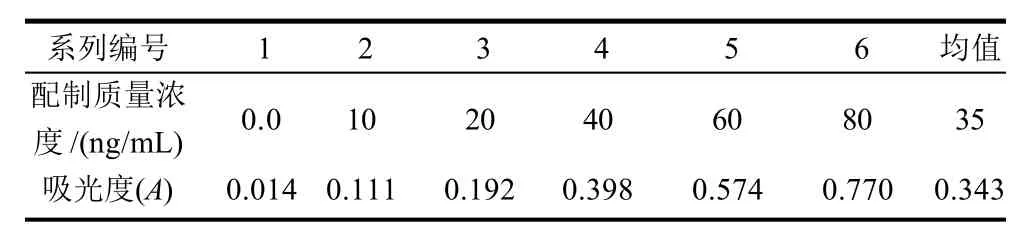
表1 铅校准曲线Table 1 calibration curve of lead
1.4 样品处理
实验猪肝样品在80℃条件下烘4h后密闭自然冷却至室温,分别称量14份1g样品于50mL高脚烧杯中,7份作为加标回收实验的非加标样品,另7份加入0.5mL标准使用液作为回收实验的加标样品。另作试剂空白3份。
采用湿式消解法,消解试样用0.5mol/L硝酸溶液定容至25mL容量瓶中。定容时的溶液温度15℃,上机检测时的溶液温度18℃。
1.5 偏差实验
测定方法按照GB 5009.12—2010《食品中铅的测定:石墨炉原子吸收法》。方法偏差实验结果见表2。
2 方法偏差不确定度来源分析及其计算模型
2.1 计算模型及不确定度来源
方法偏差SF的不确定度u(SF)评估模型:

式中:为平均回收率;f行为为加标物质与实际物质行为差异的校正因子;f回收为平均回收率与回收期望值100%的偏差的校正因子。式中右边的3个因子是方法偏差SF不确定度u(SF)的主要来源。
2.2 方法偏差不确定度的合成算式
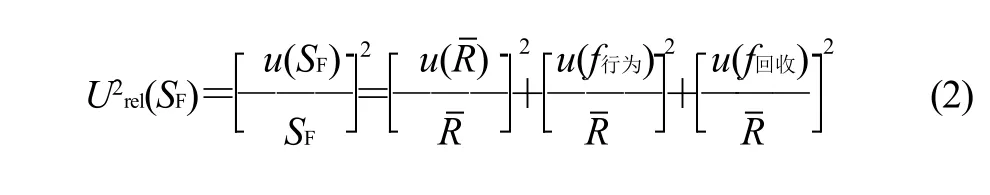
3 不确定分量的估计
3.1 平均回收率()的相对不确定度的平方u2rel():
3.1.1 计算模型及不确定度来源

式中:X标为被测物含量观测值或加标量观测值;
Xs为含量标称值或加标量标称值;f溶液为校准溶液浓度因子;f重复为回收率重复性因子。平均回收率()不确定度主要来源于式中右边的4个分量。
3.1.2u2rel()的合成算式
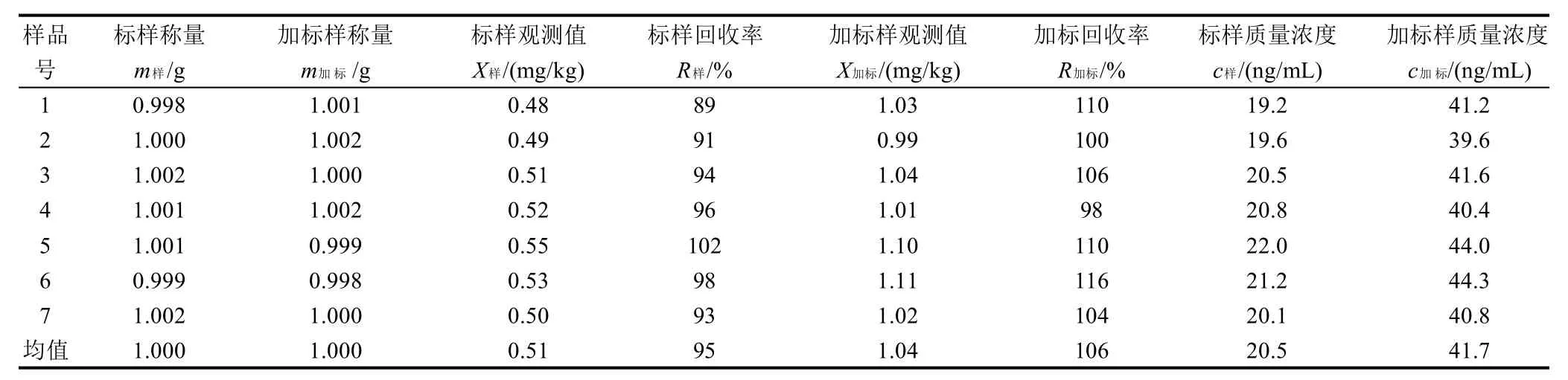
表2 方法偏差实验结果Table 2 standard deviation of methods
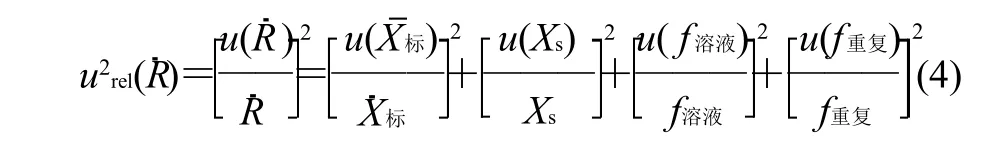
3.1.2.1 被测物加标量观测值标的相对不确定度的平方u2rel()
(1) 相对不确定度平方u2rel(X-标)的计算模型及主要不确定度来源


根据经验,体积不确定度u(V)、称量不确定度u(m)与相关系数r<0.9999的曲线拟合浓度的不确定度u(c)相比,一般可以忽略,即式(6)和式(7)中的体积项V和质量项m可忽略并代入式(5),便得到被测物加标量平均观测值X-标的相对不确定度平方u2rel(标)的简化展开式:

式中:为加标平行样曲线拟合浓度的平均值;为非加标平行样曲线拟合浓度的平均值;为试剂空白平行样曲线拟合浓度的平均值。构成被测物加标量平均观测值标不确定度的主要分量是式中右边的3个分量。
(2) 各分量的计算
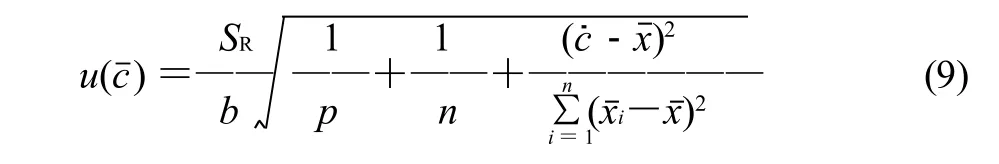
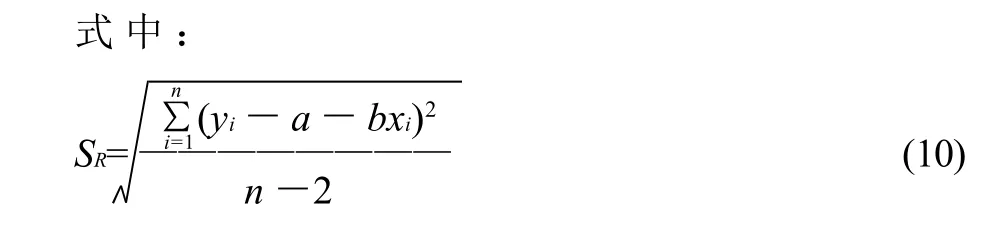
式(9)和式(10)中:c为试样的曲线拟合浓度;SR为校准曲线的剩余标准差;b为校准曲线回归方程的斜率;p为试样测量次数,本例p=7;n为绘制校准曲线的点数,本例n=6;为绘制校准曲线各浓度点数值的平均值,本例=35;xi为绘制校准曲线各点的浓度值;yi为绘制校准曲线各点的信号值;a为校准曲线回归方程的截距。
将表1、2的对应数据代入式(9)、(10)计算结果为:
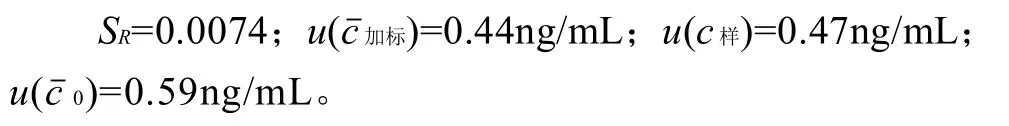
则式(8)分子上第1项和第2项的因式值分别为:

式中:V移2为移取标准使用液的体积,0.5mL;V移1为移取标准储备液的体积,1.00mL;V容1为标准使用液的定容体积,100mL;cs1为标准使用液的质量浓度,1000ng/mL;cs0为标准储备液的质量浓度,100.0μg/mL,U=0.8%,k=2;加标为样称量质量的平均值,1.000mg。
(1) 移液和定容体积V移2、V移1、V容1的不确定度u(V移2)、u(V移1)和u(V容1)
构成体积V不确定度u(V)的主要分量有3个:量器示值误差引入的不确定度u(ΔV示值);配制溶液时溶液温度偏离标准温度引入的工标体积差不确定度u(ΔV工标);使用溶液时的液温偏离配制溶液时的液温引入的温变体积差不确定度u(ΔV温变)。其中,移液体积可有工标体积差而无温变体积差,定容体积既可有工标体积差也可有温变体积差。
① 量器示值误差的不确定度u(ΔV示值):查知0.5mL分度吸量管允差±0.005mL,1mL单标线吸量管±0.007mL,100mL容量瓶±0.10mL,取三角分布k=,则:
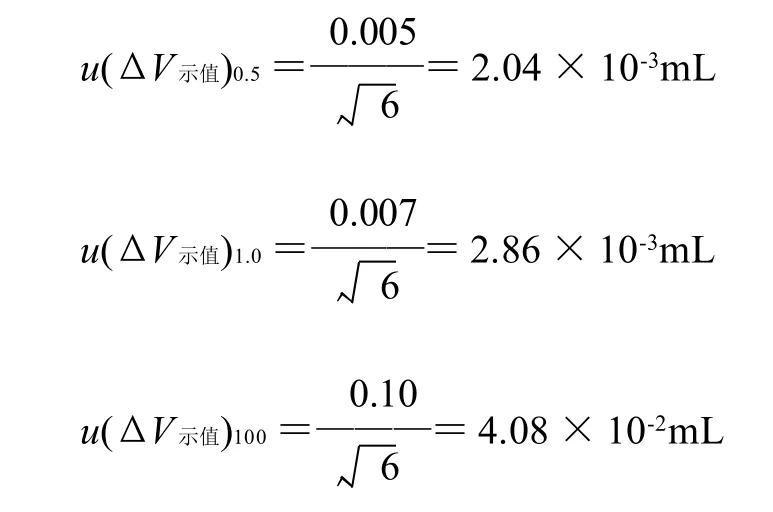
② 配制溶液时工标体积差的不确定度u(ΔV工标):由于水密度随温度的变化呈非线性,用体胀法ΔV=VβΔt(适用对象是密度随温度的变化呈线性的溶液)计算温度变动导致水溶液的体积变化是不适合的。可根据密度定义式推导出体积变化算式,再用密度修正值代替密度值便可进行准确计算:
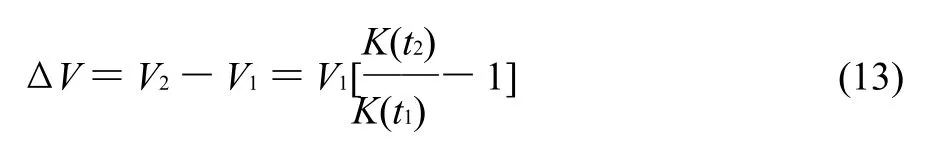
式中:ΔV为温度从t1变化到t2时的溶液体积变化;V1为溶液在t1时的体积;K(t2)-1和K(t1)-1分别为t2和t1时水的密度修正值,其倒数值可在JJG 196—2006《常用玻璃量器检定规程》和JJG 646—2006《移液器检定规程》中查得:钠钙玻璃的K(20)=1.00285;K(18)=1.00251;K(15)=1.00208;硼硅玻璃的K(20)=1.00285;K(18)= 1.00247;K(15)= 1.00200。
将对应数据代入式(13):




式中:ci为配制的校准溶液第i点的浓度;Vi为配制第i点浓度吸取标准使用液的体积;V容2为配制第i点浓度的定容体积;V移1为吸取标准储备液的体积;V容1为配制标准使用液的定容体积。
(1) 式(14)中各分量的计算
本例中,因量器示值误差取其允差、溶液配制和使用时的温度相同,所以式(14)中右边的第2项与第5项等值,且第3、4、5项已在3.1.2.2(1)④和3.1.2.2(3)节给出。
式(14)中的第1项,取6个校准点中相对不确定度最大的5号点作为评估对象:查得10mL A级分度吸量管允差±0.05mL,则:

3.2 加标物质与实际物质行为差异f行为引入的不确定度u(f行为)
3.2.1 标样回收率均值与加标回收率均值加标差异的显著性检验[13]
分别将表2中的R样和R加标数据代入贝赛尔公式算得:

3.3 平均回收率R-与期望值100%的差异引入的不确定度u(f回收)
3.3.1 差异的显著性检验

4 方法偏差相对不确定度urel(SF)的合成

5 讨 论
5.1 从3.1.2.5节可知,本例平均回收率的总不确定度为u2rel()=3.04×10-3,其重复性不确定度u2rel(f重复)=5.00×10-4,只占其总不确定度的16%,如果校准曲线的相关系数低于0.999或者回收率重复性的精密度再高一点,它便被忽略;从3.1.2.2(3)和(4)节可知,本例中证书给的储备液的不确定度u2rel(cs0)=1.60×10-5,只占加标稀释过程总不确定度u2rel(Xs)=4.22×10-5的38%,只是平均回收率总不确定度的0.5%,是一个可以忽略的分量;若将回收率的重复性不确定度u2rel(f重复)与证书给的储备液的不确定度u2rel(cs0)合成,其结果也只占回收率总不确定度u2rel()的17%;比较3.1.2.1(3)与3.1.2.5节可知,加标量观测值的不确定度u2rel(标)=2.46×10-3,占到平均回收率总不确定度u2rel()的81%,主要来源于曲线拟合浓度的不确定度。可见,值的获得贯穿于整个检测过程,过程中的每个环节都会给值的不确定度带来贡献,故平均回收率的不确定度若只考虑其重复性和标物证书这二个因素是不够的,除非其他因素与其相比可以忽略。
5.2 从3.1.2.1节可知,若回收实验的方法不同则过程不同,构成回收率不确定度的分量也不同。例如,对于加标回收法,若加入的是固体标准,则体积因素减少称量因素增加;若加标量按绝对量计不按浓度计,模型中体积因素将减少;若加入的标准经过多次稀释,则模型中将涉及更多的移液体积和定容体积。如果采用标样回收法,则实验过程与计算模型都不同于加标回收法。可见,回收率值具有与过程紧密联系的特性,以回收实验的实际过程及其计算模型为依据的评估结果具有更高的严密性和针对性。
5.3 回收率值是一个与过程密切相关的量值,没有过程便得不到回收率结果,过程不同评定结果不同,虽然其不确定度的评估对象及其过程与被测物的相似且工作量更大,但这是它的特性决定的,是应当遵守的;如果回收实验与被测物检测实验的过程与条件相同,则它们是可以共享有关分量的。
5.4 本例采用标准样品的加标实验,目的是考察被测物的加入形态与样品中的固有形态在方法中存在的行为差异。实际上它们在方法中有时是存在差异的,加标法不见得都能真实反映被测物的回收情况。故当采用加标回收法又有标准样品时,可深入考察行为偏差及其影响,否则只能假设行为因子为1。如果回收实验采用标样法,则行为偏差为零。
5.5 常见将一组实验获得的回收率数据代入近似公式的处理方法[14-16]。近似公式作为一种B类评估方法,适合用到从资料获取数据的场合。既然已由实验获得了数据,采用A类方法更合理并更具有针对性。
[1] 全国认证认可标准化技术委员会. GB/T 27404—2008实验室质量控制规范食品理化检测[S]. 北京∶ 中国标准出版社, 2008.
[2] 北京市环境保护监测中心. 环境监测测量不确定度评定[M]. 北京∶中国计量出版社, 2009∶ 49-53.
[3] 昃向君, 陈世山, 刘心同, 等. 食品安全检测实验室测量不确定度的评定与应用[M]. 青岛∶ 中国海洋大学出版社, 2007∶ 106-111.
[4] 罗珀. 标准物质及其在分析化学中的应用[M]. 李红梅, 刘菲, 李孟婉, 译. 北京∶ 中国计量出版社, 2006∶ 118-125.
[5] 李慎安. 回收率及其不确定度[J]. 中国计量, 2007(1)∶ 89-90.
[6] 林小莉, 董艳峰, 于静泉. 高效液相色谱法测定鸡肉中噁喹酸残留量的测量不确定度评定[J]. 食品科学, 2009, 30(14)∶ 219-222.
[7] 汪辉, 曹小彦, 彭新凯, 等. 高效液相色谱法测定小麦粉与大米粉中甲醛次硫酸氢钠含量的不确定度评定[J]. 食品科学, 2009, 30(12)∶205-208.
[8] 崔淑华, 郭庆龙, 刘冰, 等. 液相色谱法测定鸡肉中二氯二甲吡啶酚残留量的测量不确定度评定[J]. 食品科学, 2007, 28(12)∶ 397-400.
[9] 王莹, 张红, 曾青, 等. 气相色谱-质谱联用法测定姜中丙炔氟草胺的不确定度评定[J]. 食品科学, 2009, 30(2)∶ 176-179.
[10] 霍艳敏, 王艳丽, 王骏, 等. 高效液相色谱法测定婴幼儿乳粉中烟酰胺的不确定度评定[J]. 食品科学, 2011, 32(16)∶ 330-333.
[11] 魏大伟, 程江山, 郑玉芝. 液相色谱法测定饼干中日落黄含量的测量不确定度评定[J]. 食品工业科技, 2011, 32(6)∶ 414-417.
[12] 付登洲, 杨雪娇, 黄伟. HPLC法测定乳制品中三聚氰胺含量的不确定度评定[J]. 食品研究与开发, 2011(2)∶ 108-112.
[13] 邓勃. 数理统计方法在分析测试中的应用[M]. 北京∶ 化学工业出版社, 1984∶ 70.
[14] 杨洋, 徐春祥, 车文军. 高效液相色谱法测定奶粉中的三聚氰胺及其不确定度分析[J]. 食品科学, 2010, 31(4)∶ 250-253.
[15] 林媚, 平新亮, 姚周麟. 茶叶中铜含量测定的不确定度分析[J]. 计量与测试技术, 2010, 37(8)∶ 63-68.
[16] 徐文峰. HPLC 法联测番杏中 VC、VB2和VPP的不确定度评定[J]. 湖北农业科学, 2010, 49(2)∶ 443-446.
Uncertainty Evaluation of Recovery in the Measurement of Lead in Pigs Liver by GF-AAS
ZHAN Yong-ge1,GONG Jian1,HUANG Xiang-yan2
(1. Center of Analytical and Testing, Guangzhou University, Guangzhou 510006, China;
2. Testing Center for Water Quality, Zhongshan City Water Supply Co. Ltd., Zhongshan 528403, China)
Using the actual process of spiking standard recovery experiments and computing model, the total uncertainty of lead measurement using graphite furnace atomic absorption spectrometry pig,s liver was evaluated. The results shows that the repeatable uncertainty of an average recovery rate composes only 16% of the total uncertainty; standard stock solution composes only 38% of the uncertainty of the spiked dilution process, which is 0.5% of the average recovery rate, whereas the uncertainty of plus scalar observations composes major part of the total uncertainty, accounting for 81%, mainly from the curve fitting the concentration uncertainty. There are higher rigor and relevance if the assessment of recovery rate bases on actual process and computing models.
chemical detection;food inspection;measuring deviation;recovery;uncertainty
TB99
A
1002-6630(2012)10-0155-06
2011-06-06
国家自然科学基金青年科学基金项目(40903040)
占永革(1957—),男,高级工程师,硕士,研究方向为分析测试。E-mail:zhanyongge@163.com

