基于chirp-z变换的斜视FMCW-SAR非线性尺度变换算法

于彬彬 刘 畅 王岩飞

①(中国科学院电子学研究所 北京 100190)

②(中国科学院研究生院 北京 100039)

1 引言

随着SAR技术的高速发展，SAR小型化的需求越来越迫切。小型SAR技术的难点在于载荷体积和重量的控制。对于传统脉冲体制的SAR系统，发射机的瞬时功率较高，相应的硬件的体积和重量较大，很难小型化。调频连续波合成孔径雷达(Frequency Modulated Continuous Wave Synthetic Aperture Radar,FMCW-SAR)的开发与应用解决了上述问题[1－3]，FMCW-SAR 的发射信号为连续波信号，因此和传统脉冲体制的SAR系统相比，发射机的瞬时功率较小，发射机的体积与重量也相应降低。

FMCW-SAR与传统脉冲SAR回波信号在距离向略有不同，但成像算法类似。FMCW-SAR的成像算法包括距离多普勒算法(Range-Doppler Algorithm,RDA)[4]、频率尺度变换算法(Frequency Scaling Algorithm,FSA)[5]、距离徙动算法(Range Migration Algorithm,RMA)[6]等。RDA是基本成像算法，运算量小但成像精度低；RMA是精确成像算法，但其实际成像精度取决于插值运算的精度，成像精度越高，则运算量越大。相比而言，FSA的特点介于两者之间，其核心思路是在多普勒域进行线性频率尺度变换，较为精确地校正距离徙动[7]。与FSA原理类似，chirp-z变换方法也是一种通过引入线性调频信号进行线性尺度变换的算法，其原理稍有不同，但处理信号的结果是一致的[8]。

当FMCW-SAR工作在斜视模式时，回波信号在多普勒域形成的距离徙动项具有非线性的形式。原始的FSA和chirp-z算法只能对该距离徙动项进行线性校正，该校正仅对场景中心处的点目标是精确的，距场景中心线越远，其校正误差越大，最终的聚焦效果也越差。

文献[9]提出了一种斜视SAR改进FS算法，该算法对去斜率接收的回波信号进行处理，可以直接应用于FMCW-SAR。由于该算法基于FS算法，在计算过程中需要进行5次距离向FFT或IFFT，运算量较大，而采用chirp-z变换则只需要4次；同时，频率尺度变换操作会造成距离向频谱混叠，需要进行升采样操作，该算法中斜视角越大其升采样率越大，运算量也越大，而采用chirp-z变换只需升一倍采样，更适合大斜视角成像。

针对以上问题，本文提出一种斜视 FMCWSAR的非线性尺度变换 chirp-z算法，该算法可以对多普勒域回波信号的距离徙动项进行非线性校正，从而得到更好的成像效果。本文首先建立斜视FMCW-SAR信号模型，分析该模式下FMCW-SAR回波信号特点，在原始chirp-z算法的基础上提出本文算法，该算法在chirp-z变换中引入三次相位，对回波信号进行非线性尺度变换，更精确地进行二次距离压缩和校正信号的距离徙动项，相比原始chirp-z算法得到更高的成像精度。最后，通过点目标仿真对本文提出算法的有效性进行了验证。

2 回波信号模型

图1为FMCW-SAR斜视模式下的几何关系图，阴影区域表示了地面上测绘带的范围，O为慢时间tm的零时刻载机位置，RC为场景中心到载机航线的垂直距离，v为载机速度。

若点目标沿方位向位于x处，到雷达载机航线的垂直距离为RB，则其去调频接收回波信号为[10]

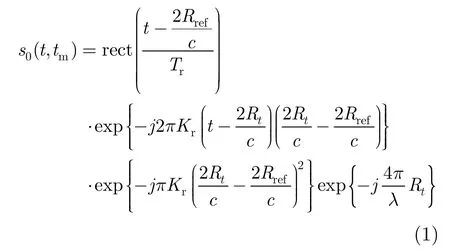
其中

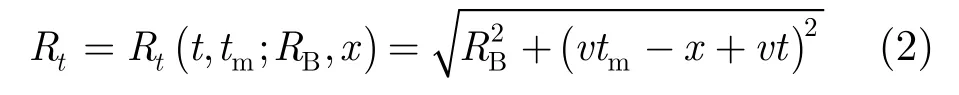
图1 斜视FMCW-SAR几何关系图

式(1)中Tr为接收回波总持续时间，Kr为发射线性调频信号的调频斜率，Rref为去线性调频的参考距离，并假设它对应的延迟时间与接收回波的中心采样时间相同。式(1)中的第2个相位项是去斜率接收方式中独有的残留视频相位(Residual Video Phase,RVP)项[11]。

式(2)中Rt随快时间t变化，产生快时间走动项。FMCW-SAR与传统脉冲体制SAR相比，拥有大的脉冲持续时间，则并不成立，也即“走-停”假设失效，需要额外的步骤校正该快时间走动项[12]。下式为快时间走动项的校正式：

其中fa是多普勒频率变量，上式中FFT及IFFT均为1维方位向操作。

由驻相点法可以得到上式的另一种表示方法：

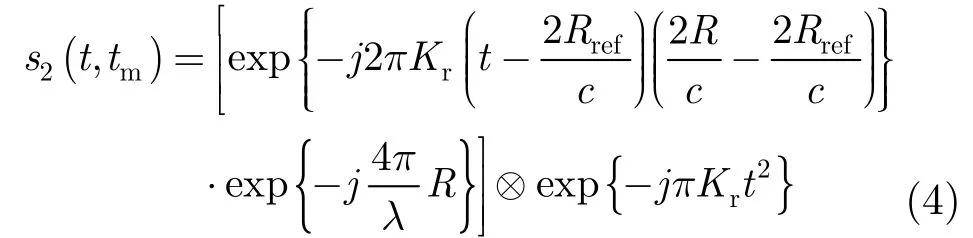
使用驻相点法，对上式作方位向FFT，可得多普勒域信号：

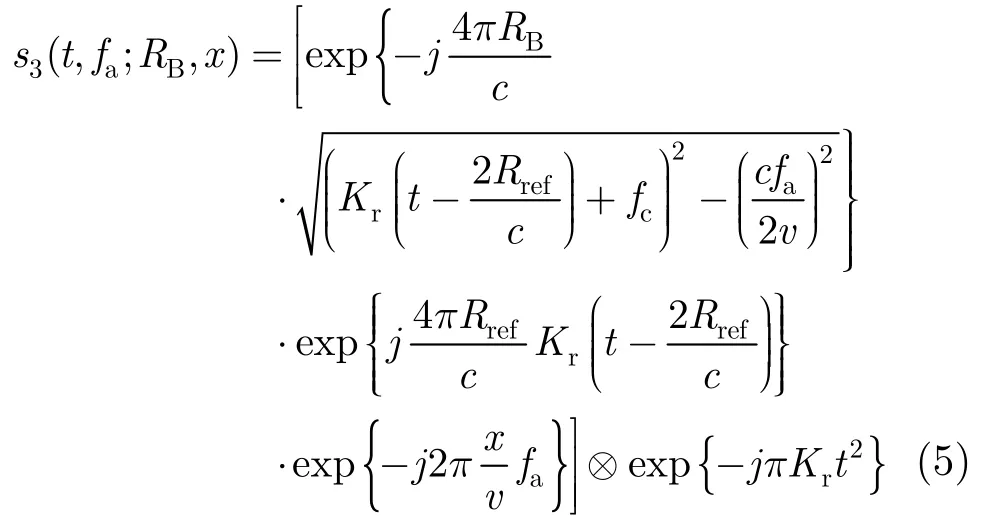
3 非线性chirp-z变换算法

在介绍本文非线性chirp-z变换之前，首先需要对式(5)进行处理。去除其中的卷积项，并与参考距离上点目标的匹配函数相乘，得到

上式中FFT与IFFT均为距离向的操作。将式(6)的第1个相位项写成如下形式：

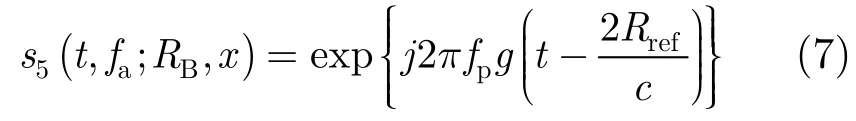
其中

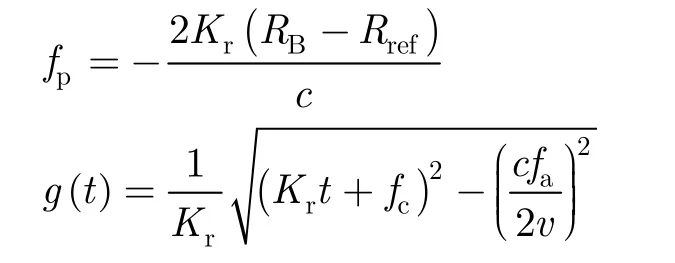
原始的chirp-z线性尺度变换式为[13]

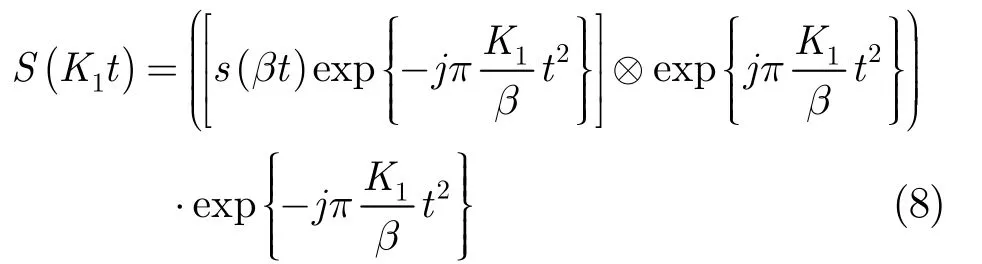
其中S(fr)为s(t)的频域形式，为尺度变换的比例因子。当距离向采样率为fs，采样点数为Nr时，取可以满足S(K1t)和S(fr)具有相同数字信号的条件。

基于上述原始chirp-z变换式，通过引入非线性调频信号 e xp{−j2πh(t)}可以对式(7)实现非线性尺度变换：

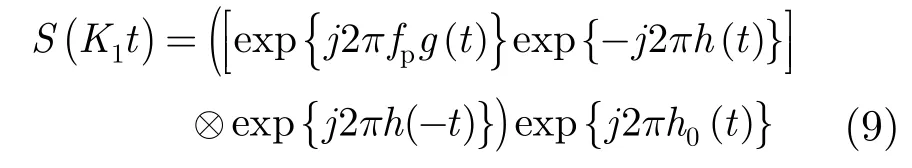
其中h0(t)是和h(t)相关的相位函数。S(fr)为所需信号s(t)=exp {j2πfpt}的频域形式，则有S(K1t)=。对于g(t)，假设存在一个h(t)使得上式成立，下面求解h(t)：

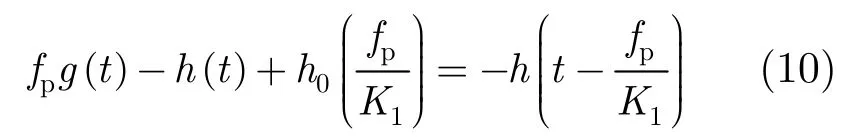
对t求导得：

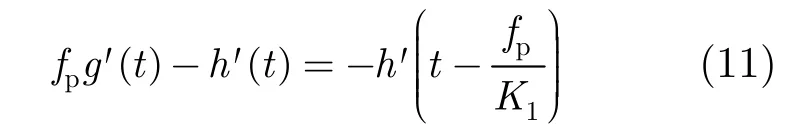
即

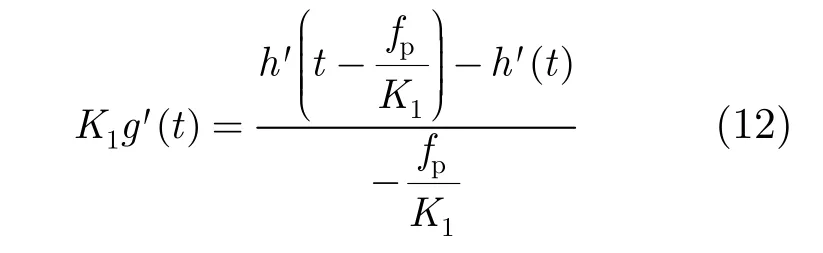
当fp较小时，上式变为

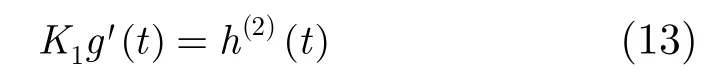
为使式(9)右边第一步乘法不产生频移，应有h′(0)=0，则应使h′(t)=K1(g(t)−g(0))，令h(0)=0，可以通过积分解出：

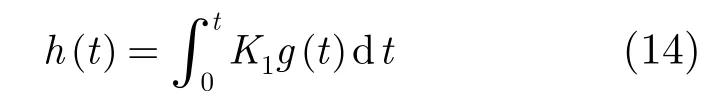
再令t=0 ，解出：

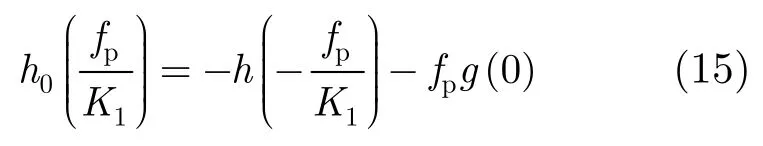
可以看出，对于给定的函数g(t)，可以解出式(9)中所需函数h(t)和h0(t)。然而，对于不存在解析式，只能将g(t)泰勒展开，截取若干项对h(t)进行近似求解。特殊地，当仅取常数项和一次项时，求出，这就是原始的 chirp-z算法。但当雷达波束斜视角较大时，g(t)泰勒展开式的二次及以上项不能忽略，此时采用原始chirp-z算法将引入较大相位误差，造成成像精度降低。

经过分析，斜视角较大时，取g(t)泰勒展开式二次及以下项可以满足要求，如下式：

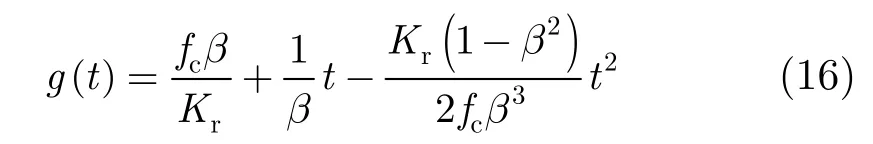
积分求出h(t)：

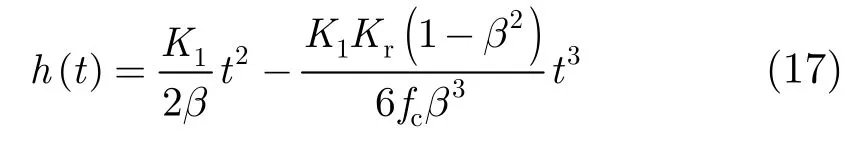
将式(16)，式(17)代入式(15)，得到

将式(16)～式(18)代入式(9)验证，前后卷积项之间的相位误差为

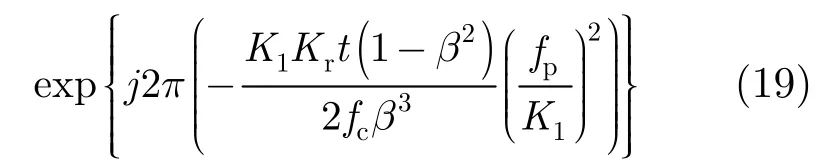
上式相位越小，卷积操作匹配的效果就越好。上式中最大误差相位为

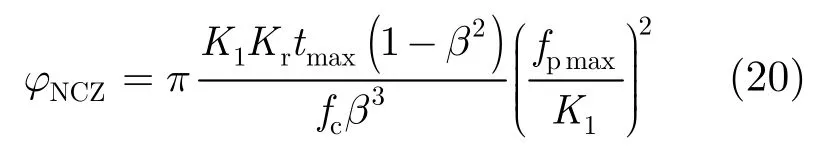
其中tmax=Nr(2fs),fpmax=Bc2,Bc为接收回波有效带宽，且满足Bc＜Fs。

在一定斜视角下，如果使用原始的chirp-z算法成像，将得到如下的聚焦误差：

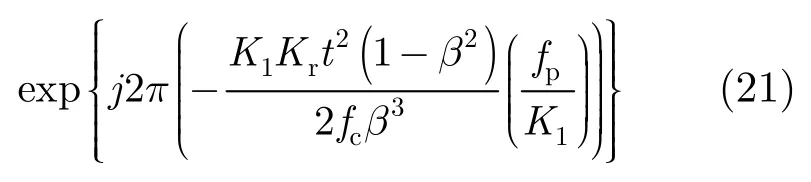
其最大误差相位为

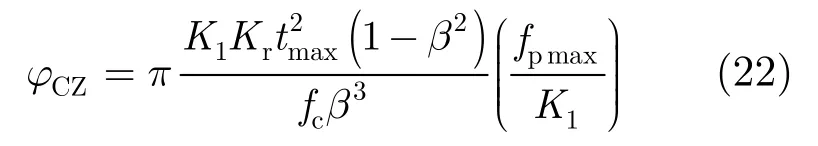
比较式(20)与式(22)，二者比值为

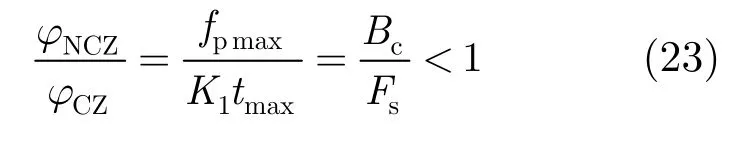
由此可见式(20)中最大误差相位比式(22)小。也就是说，本文提出的非线性chirp-z变换相对于原始chirp-z变换可以更好地补偿距离徙动校正时的误差相位，提高算法的成像精度。

对式(6)进行上述非线性chirp-z变换处理之后，再进行方位向IFFT即可得到成像结果。

4 仿真结果

本节通过点目标成像验证上述分析。仿真采用表1中的参数，模拟回波包含5个点目标。对于同一模拟回波信号，分别采用原始chirp-z算法和本文提出的非线性尺度变换chirp-z算法，得到成像结果。5个点目标的非线性chirp-z算法成像结果见图2。

表1 仿真参数

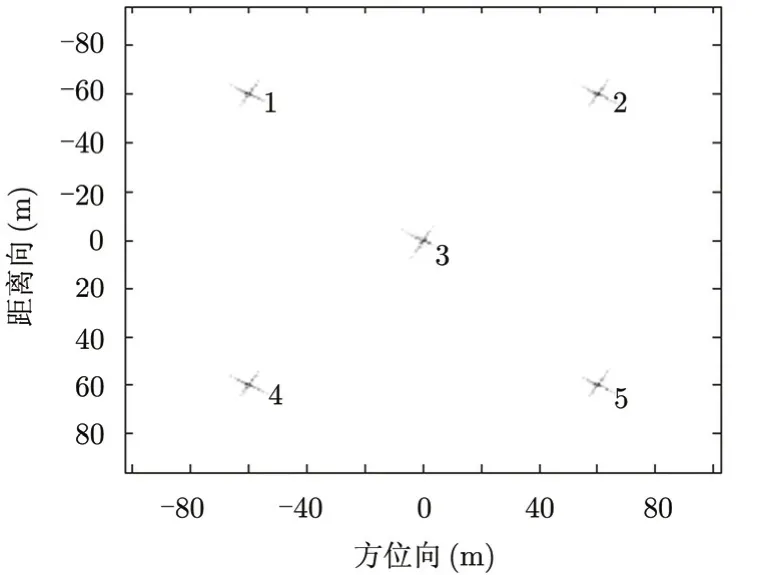
图2 5个点目标的成像结果

选取图2中的3个点目标进行成像精度分析，图3，图4，图5分别给出了使用原始chirp-z算法和非线性chirp-z算法成像后的2号、3号、4号点目标的2维分辨率。表2为它们的脉冲响应的3 dB宽度。可以看出，对于图4中场景中心的点目标，两种算法的成像结果非常接近，而在图3和图5的分图中，图(c)比图(a)中的分辨率高，图(b)和图(d)中的分辨率较为接近。同时，表2中的数据也可以说明，改进后的算法与原始算法相比，对场景中心线以外点目标的方位向压缩结果较为接近，而距离向的分辨率能够提高大约30%。

从式(19)和式(21)中可以解释上述仿真结果。式(21)中原始chirp-z算法的误差相位是快时间的线性调频信号，它相当于距离压缩时的不完全匹配，造成距离向的散焦。式(19)中非线性尺度变换 chirp-z算法的误差相位是快时间的线性信号，不影响距离向的聚焦，该误差的存在使得本文算法未能显著提高方位向分辨率。

使用原始chirp-z算法和非线性chirp-z算法成像后的图像，在2号、3号、4号点目标附近的图像强度对比度如表3。由表3可以看出，相比原始chirp-z算法，非线性尺度变换chirp-z算法可以将场景中心线以外区域成像结果的图像对比度提高大约50%。

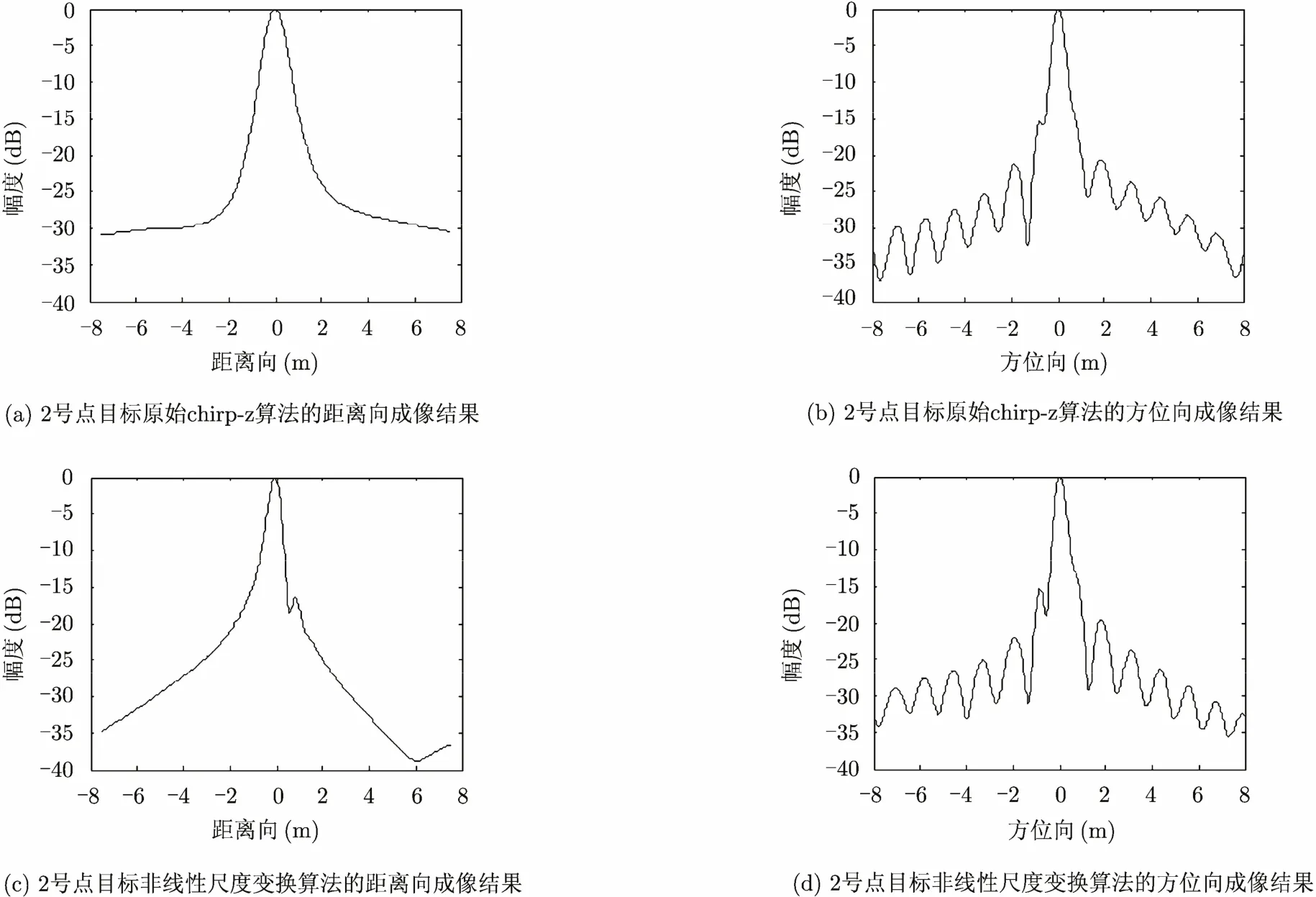
图3 2号点目标的成像结果

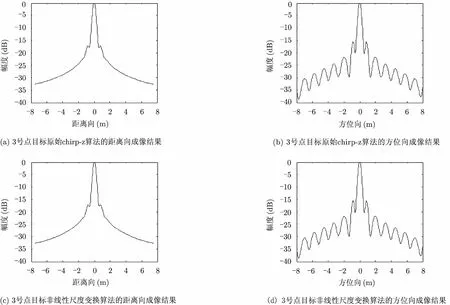
图4 3号点目标的成像结果

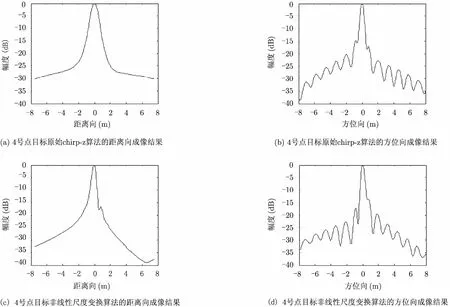
图5 4号点目标的成像结果

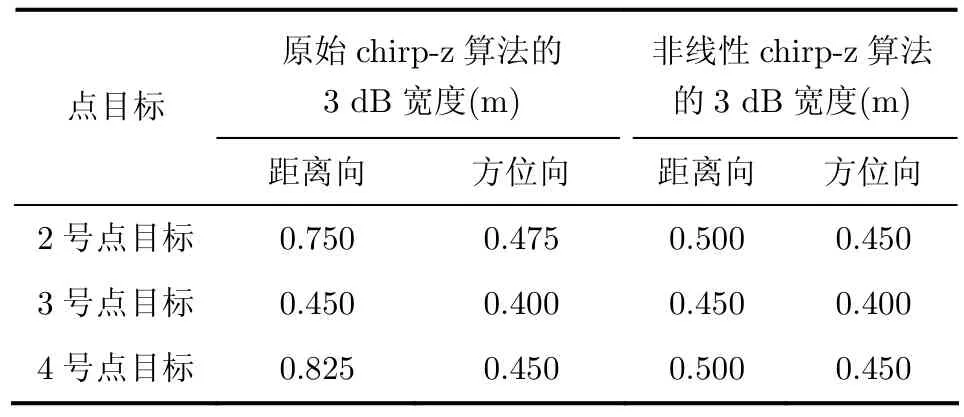
表2 两种算法点目标冲击响应函数的3 dB宽度比较

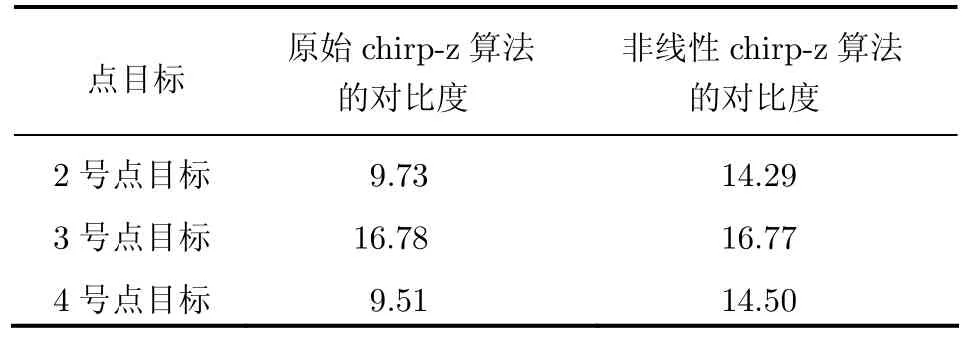
表3 两种算法成像结果中点目标附近的图像强度对比度

以上仿真结果与理论推导和分析结论一致，验证了本文提出的非线性尺度变换 chirp-z算法对提高斜视FMCW-SAR成像效果的有效性。

5 结论

本文针对FMCW-SAR在斜视模式下聚焦精度降低的问题，提出一种非线性尺度变换chirp-z算法。该算法对原始chirp-z算法进行改进，通过引入非线性调频信号，对回波信号进行非线性尺度变换，可以降低距离压缩和距离徙动校正的误差，提高雷达成像精度。从仿真结果可以看出，采用本文提出的非线性 chirp-z算法对点目标模拟回波的成像结果与原始chirp-z算法相比，距离向分辨率和图像对比度均得到明显提高，方位向分辨率保持不变。