带HALL直线电动机的低速驱动调整与优化技术

陈东生 吉 方 蓝 河

（中国工程物理研究院机械制造工艺研究所，四川绵阳 621900）

与旋转电动机相比，直线电动机驱动消除了中间传动机构，结构简单、摩擦小、无齿隙误差、响应快、精度高，但直线电动机中间环节的消除使得外部干扰无衰减地直接作用于直线电动机，同时采用静压支撑，其系统阻尼系数很小，这使得定位机构对振动干扰更加敏感。此外，直线电动机存在固有的推力波动，是影响伺服控制精度的主要原因，这种推力波动将引起速度波动、机械振动和噪声，甚至导致系统失稳。因此，需要从系统设计、硬件性能、伺服精密调整方面来提高和优化直线电动机的驱动特性与控制系统的鲁棒性，减小外来扰动对伺服系统的影响，提高伺服系统刚度;提高静压支撑下直线电动机驱动的直线平台的高动态特性、高精度定位、高稳态特性。本文就在气浮支撑的直线电动机驱动的设计与调试过程中遇到的问题进行分析，并提出解决办法，以供大家借鉴。

1 直线电动机驱动系统构成

本直线电动机驱动系统用于驱动气浮支撑的精密定位台，需要实现平台的高精度定位。直线电动机伺服驱动系统采用高精度直线光栅尺进行闭环位置检测，整个系统设计为基于观察器的三层控制模式:即采用具有位置反馈、速度反馈和电流反馈的三闭环结构形式，如图1所示。

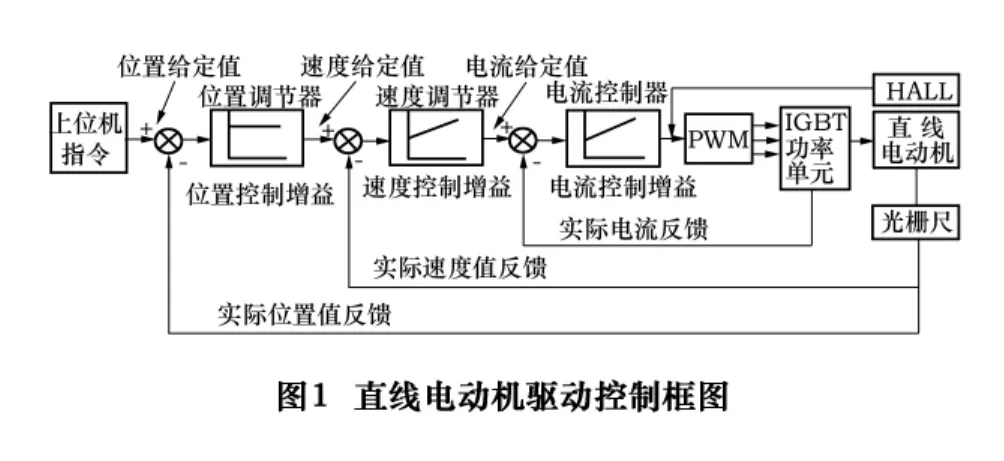
系统采用无铁芯直线电动机，光栅尺采用HEIDENHAIN公司的敞开式高精度光栅尺，其分辨率为0.005 μm，将光栅尺位置信号直接反馈到驱动器，在驱动器内部实现全数字的位置环、速度环和电流环控制，电流环通过PWM控制信号到IGBT功率单元，然后通过U、V、W实现对电动机的驱动。驱动器通过HALL信号进行换相。

2 HALL换相的故障诊断

系统采用的测量元件为增量式光栅尺。增量式光栅尺分为带换相信号的增量式编码器和普通的增量式编码器，带换相信号的增量式编码器除具备ABZ输出信号外，还具备互差120°的电子换相信号UVW，UVW各自的每转周期数与电动机转子的磁极对数一致。本系统的增量式光栅尺是普通增量式，它提供两相正交方波脉冲输出信号A和B，以及零位信号Z，它不具备UVW相位信息，而Z信号也只能反映一圈内的一个点位，不具备与电动机相位与转子相位对齐潜力，为此，电动机的换相是通过直线电动机动子上的固定HALL传感器来进行换相。

在直线电动机的性能调整中遇到了一个棘手的问题，直线电动机无法换相。其故障现象:系统配置过程中出现故障，报警提示为HALL Commutation error，应该是HALL的换相故障。

故障诊断分析:

（1）对于伺服系统的调试，首先想到的是硬件接线错误导致HALL的相序有误。最先排查的就是硬件接线，检查接线是否错误，在仔细核对HALL传感器的接口信号与驱动器的接口信号匹配关系、测试线缆没有断点后，确认接线没有问题，故障原因不是接线的问题。

（2）硬件接线没有问题的话，考虑是否是软件上故障，即设置参数不对，驱动器的参数配置错误导致的。电动机在进行反馈系统设置时，需要设置编码器分辨率、换相方式、换相角度、换相的方向、传感器极性、传感器Z信号是否有效等。但通过软件手册仔细分析并尝试多次更改参数，其故障依然存在。

（3）软件与电气连接都没有问题，考虑是否是电气信号干扰导致HALL信号不正常，导致无法进行换相角检测。将其他电气系统均关闭，同时驱动器的调试也没有给主电源上电，只是驱动24 V给电。另外，光栅的线缆、HALL的信号电缆均采用的原装电缆，是不存在干扰问题的。

（4）参数配置没错、硬件接线也是对的，要么是HALL传感器没有信号，要么驱动器没有检测到信号。我们首先检测HALL是否正常，即HALL传感器是否具有硬件故障。图2是在慢速推动带直线电动机的平台后，用示波器对3个HALL:HA、HB、HC的信号进行检测后得到的波形。如图2所示。HA与HC的波形幅值较小，HA约为0.8 V，HC约为0.7 V，并且有波动，难道是HALL传感器的硬件故障，导致HALL信号幅值太小而无法检测?

（5）考虑通过驱动器能否检测到HALL信号，通过驱动器的调试软件来监测其HALL信号，驱动器内可以检测到该信号，并且与示波器的HALL信号检测对比，虽然波形不是太好，但信号是有输出的，并且匹配得也很好。到此就可以排除HALL传感器的硬件故障，同时排除了驱动器信号监测故障。

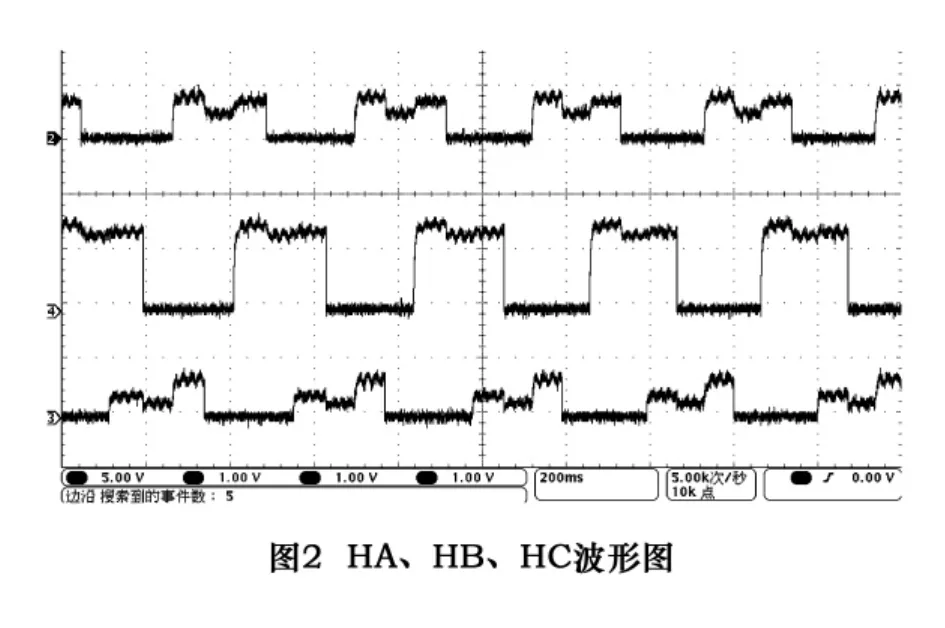
（6）到此我们得出HALL信号是没有问题的，但为何会报警HALL换相故障呢?

电动机的换相是需要3个HALL传感器:HA、HB、HC，它们按电角度120°进行分布，其供电电源是直流5 V电源，驱动器通过对3个HALL信号的组合来知道电动机所处的位置，以决定何时对UVW进行换相，那么就只有HALL的信号位置与UVW之间的位置关系不对会导致该故障。

将3个阻值相等的电阻（2 KΩ）接成星型，如图3所示，然后将星型连接的3个电阻分别接入电动机的UVW三相绕组引线，以示波器观察电动机U相输入与星型电阻的中点，就可以近似得到电动机的U相反电势波形;通过测量 U、V、W三端与公共端之间的波形和HA、HB、HC之间的波形关系。如图4～6所示。

从这3张波形图中发现，HALLA一出现上升沿，V相电压开始上升;HALLB一出现上升沿，U相电压开始上升;HALLC一出现上升沿，W相电压开始上升;它验证了直线电动机的HALL与电动机的相位关系是没有错的。

（7）到此能够考虑到的故障原因都已经排除了，但问题仍然没有得到解决。

尝试是否是厂商提供的参数与配置有问题，将HA与HB、HC之间的信号更换一下，当将HA与HB更换后，发现报警消失了，但无法伺服enable，在某个位置可以enable，但运动到HALL位置有变化的地方就又会报错。从这里可以分析得到还是HALL之间的关系不对。由于我们无法知道驱动器内部如何去匹配这个关系，因此再次阅读分析其技术手册，发现HALL是可以转换方向的。通过对hall转换方向设置后，报警消失了，但仍然无法伺服 enable，报Comutation error;从设置中发现还可以转换comutation的方向，转换换相方向后，伺服enable有效了。

（8）但该设置下运动速度较高时仍然会出现报警，报电流过大错误。这是由于换相角不准确的缘故，可以通过自动设置换相角，但自动设置无法通过。因此考虑采用手动来设置换相角，通过前面的分析，在HALLA一出现上升沿，V相电压开始上升;HALLB一出现上升沿，U相电压开始上升;HALLC一出现上升沿，W相电压开始上升;可以判断它的换相角应该是0°。将换相角设置完成后，在快速运行时通过电流监测，运行过程中电流变化不大。至此，HALL调试的故障得以全部排除。

3 低速驱动性能优化

直线电动机的低速驱动性能优化的最主要目的就是让机电系统在低速下匹配达到最佳，以获得最优的稳态性能和动态性能。通过调试中遇到的问题，总结出直线电动机的驱动性能主要受以下几方面的影响。

（1）测量元件分辨率

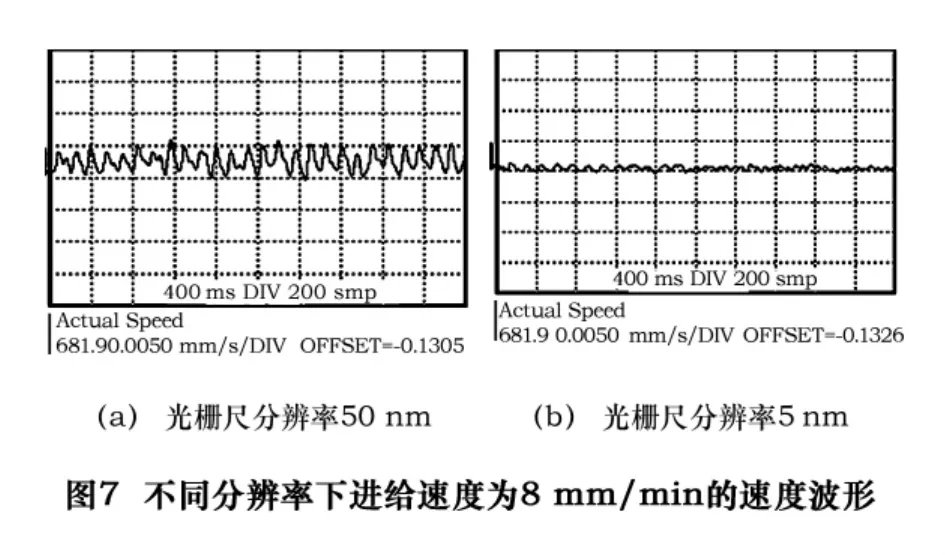
直线电动机的测量反馈系统一般是光栅尺。一般来讲，分辨率越高，直线电动机的反馈输入越准确，其控制的精度就越高。如图7所示，在分辨率为50 nm下速度波动达到了0.3 mm/min，而当分辨率为5 nm时，速度波动减小到0.07 mm/min。

（2）PWM控制的开关频率

在数字控制交流伺服系统中，制约电流环带宽的因素主要包括功率器件的开关频率和A/D采样时间、计算处理、PWM占空比更新等数字控制延时。提高PWM控制的开关频率会大大提高系统的伺服带宽，同时可以减小电流的纹波。如图8，32 kHz下的电流纹波比8 kHz的要小得多。同时它能减小低速运行时的波动。

（3）外界力的干扰

直线电动机中间环节的消除使得外部干扰无衰减地直接作用于直线电动机，同时采用静压支撑，其系统阻尼系数很小，这使得定位机构对振动干扰更加敏感。此外，直线电动机存在固有的纹波推力扰动、齿槽推力波动、端部效应扰动、永磁体磁链谐波扰动以及外界负载阻力扰动，它是影响伺服控制精度的主要原因。这些波动将引起速度波动、机械振动和噪声，甚至导致系统失稳。

比如导轨的密封风琴罩对直线电动机的速度波动影响很大。如图9，速度曲线中的尖峰就是由风琴罩的移动引起的。主轴在没有做动平衡前，在390 r/min的速度下对直线电动机的速度波动影响达到了2.4 mm/min，而此时直线电动机的运行速度为零。如图10所示。

（4）先进伺服算法

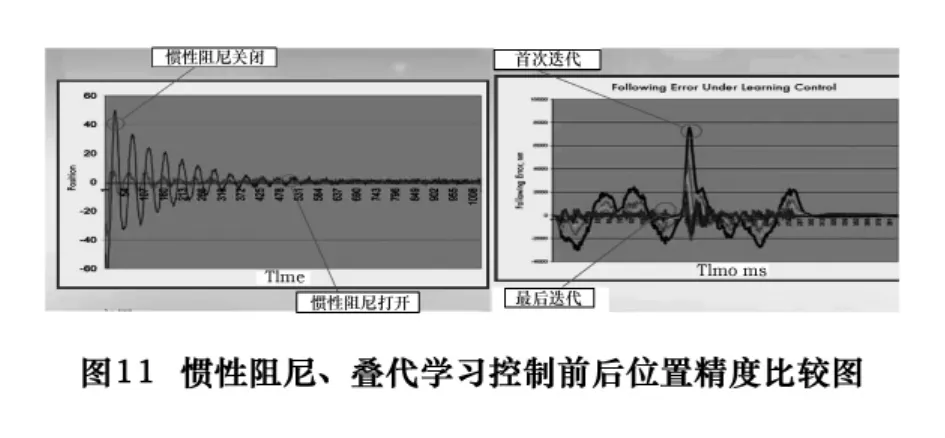
采用高级控制算法，如采用带前馈的PID伺服控制算法、谐波消除控制、叠代学习控制、惯性阻尼控制等可以提高直线电动机的控制精度。如图11，惯性阻尼控制策略是在控制算法中增加两个阻尼前馈控制:速度前馈阻尼和电流前馈阻尼，它在控制算法中起到一个类似机械阻尼的作用，可以大大提高系统的动态性能、增加速度稳定性、缩短定位时间。迭代学习控制是控制器采集前段运动的数据，通过对对象参数的辨识来自动调节控制器的参数，并将其用于以后的运动控制中，通过迭代学习，其运动可以被不断地学习与优化，从而减小运动的跟随误差，提高动态精度。

4 结语

通过以上的调整分析，得出以下结论:

（1）直线电动机的驱动调试中HALL换相的调试是比较棘手的，需要在了解换相原理的基础上对硬件性能和参数匹配进行仔细的分析与诊断。

（2）高分别率光栅尺反馈对提高直线电动机的低速性能是有益的。

（3）PWM开关频率相对提高会减小电流纹波，同时减小控制电流的波动，提高速度波动精度。

（4）直线电动机低速下运行精度，外界力干扰的影响很大，尤其要提高机床自身的共振频率、减小防护罩、外界振动对系统的影响。

（5）采用带前馈的PID伺服控制算法、谐波消除控制、叠代学习控制、惯性阻尼控制等可以提高直线电动机的低速控制精度。

［1］M．Iwasaki and N．Matsui．Observer－ based friction compensation in servo drive system［C］．4th International Workshop on Advanced Motion Control IEEE．Japan．Mie University，Tsu－Ciy．1996，344－348．

［2］Moghani J S，Eastham J F．The dynamic response of linear brusgless D．C．motor［J］．IEE Proceedings of Electric Power Applications．2005．

［3］陈娟．伺服系统低速特性与抖动补偿研究［D］．长春:中科院长春光学精密机械与物理研究所，2001．

［4］郭庆鼎．数控机床直线伺服驱动控制的若干问题与展望［J］．沈阳工业大学学报，2006．