基于S型检验试件的数控机床动态性能辨识新方法*

杜 丽 崔浪浪 赵 波 谭 阳 王 伟

（电子科技大学机械电子工程学院，四川成都 611731）

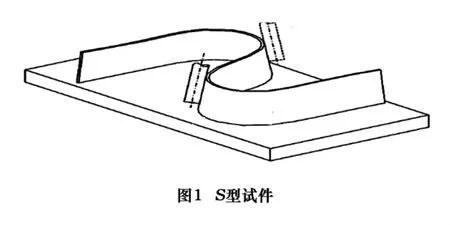
机床动态性能直接影响着机床的加工精度。S型试件是新近提出的一种校验机床动态性能的检验试件，如图1所示。试件曲率随表面形状变化而变化，在拐角处具有开闭角转换特征，通过切削S型试件可以在一定程度上反映出五轴联动数控机床动态性能。但是，关于S型试件反映的机床动态因素以及彼此间的对应关系未见之于报道。

误差溯源是通过对机床加工误差间接估计机床性能的重要方法。Lai等人从DBB法检测出发，发展了诊断数控机床导轨非线性建模分析方法［1］;范晋伟提出了十四线法［2］;赵小松等提出了九线法［3］;东京大学Matsushita开展了针对NAS979试件的误差分离，剥离出了试件型面误差中反映的六项机床几何误差［4］;东京农工大学Tsutsumi提出了四角锥台试件，可以辨识出机床的圆度、直线度、垂直度和平行度加工误差［5］。上述方法仅仅只针对了数控机床的单项几何误差辨识，并未涉及到对机床性能产生重要影响的动态因素辨识。

机床的动态性能与S型试件型面加工误差之间存在着复杂的非线性映射关系，要建立起准确的数学模型对机床动态因素进行辨识非常困难。BP神经网络强大的函数逼近能力、自学习、自适应性为数控机床动态因素误差辨识提供了一条有效的途径。为此，提出了一种通过检测S型试件切削形貌，利用BP神经网络理论及模糊理论完成数控机床各动态因素的误差辨识的新方法。

1 S型型检验试件切削仿真建模

1．1机床单运动轴运动轨迹分析

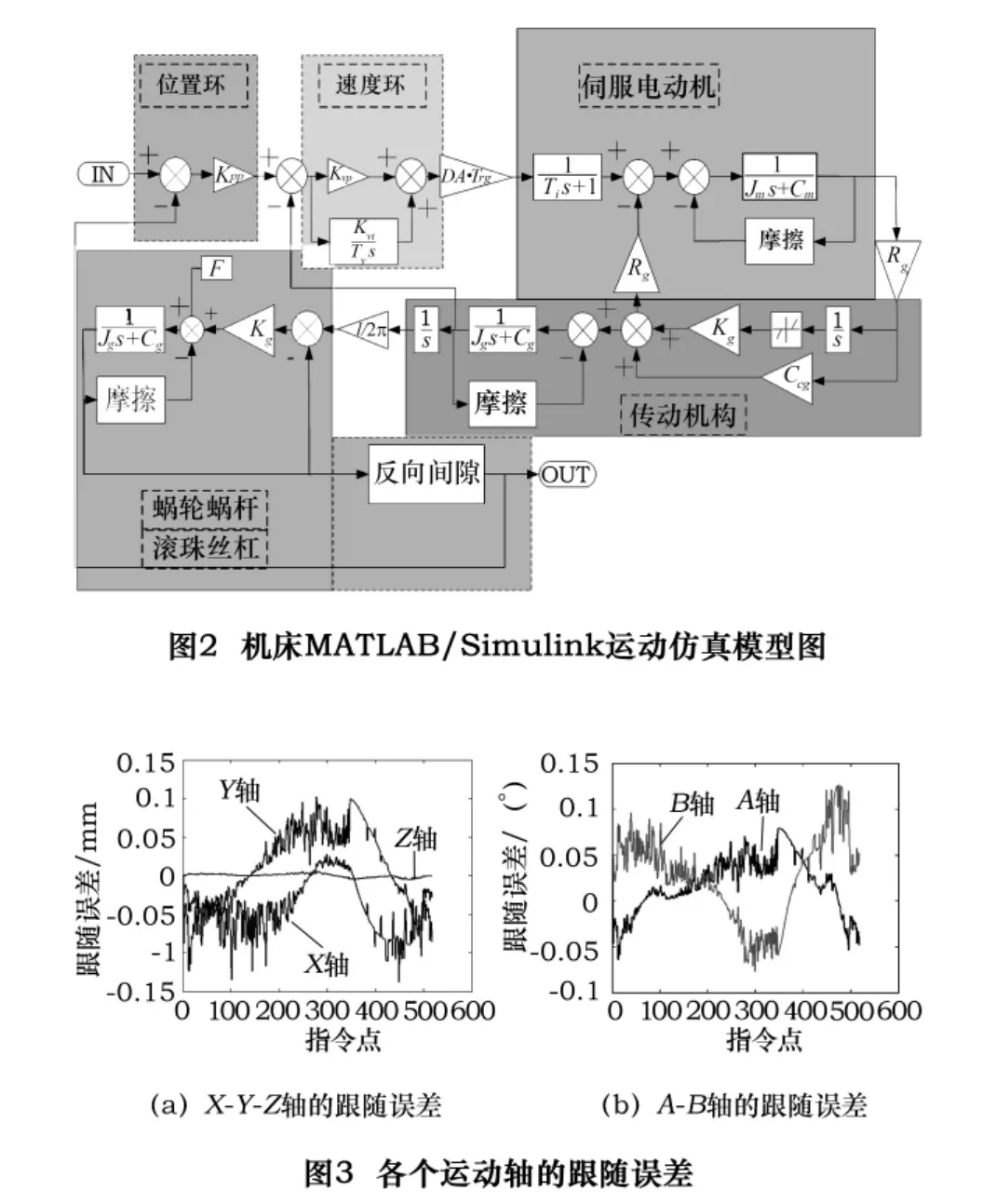
数控机床的动态误差主要是由于切削过程中机械、控制系统的整体联动而产生的，机床的基本运动结构以及伺服系统各轴协调性是影响机床动态精度的主要因素，为此，采用传递函数误差建模方法分析机床的动态跟随误差。输入的机床运动指令经位置环节、速度环节、电动机环节，最终驱动机械环节，实现数控机床的切削运动。各个环节可由相应的比例、积分或微分函数表示。图2所示是在MATLAB/Simulink中建立的机床单轴运动仿真模型，基于特定的机床可以分析变参数影响下的各运动轴跟随误差。图3a是X、Y、Z三个平动轴的跟随误差，图3b是A、B两个转动轴的跟随误差。

1．2 多轴联动运动仿真分析

数控机床中由动态误差因素产生的各轴运动轨迹误差叠加在一起构成了刀具的实际运动轨迹，由多体系统运动学建模耦合而得［6］。如图4所示是AB刀具两摆的机床拓扑结构图，可以用特征矩阵表示多体系统中体间的相对位置和姿态。

首先，建立低序列矩阵，设定惯性参考系B0，选取工件为B1体，然后远离B1的方向按自然增长数列，依次为各体编号，低序列矩阵可以通过下列计算公式得到。

任选体Bj为系统中任意典型体，体Bj的n阶低序体的序号定义为:

式中:L为低序体算子，称体Bj为体Bi的n阶高序体，满足:

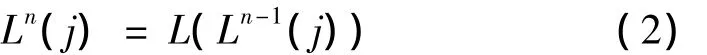
初始条件为:

由此可以计算出机床的各阶低序体阵列。

然后，采用齐次列阵表示各体的位置和矢量姿态，在多体系统中建立广义坐标系，用4×4阶齐次方阵表示体间在广义坐标系中的位置坐标和姿态方位的变换。多体系统在理想条件下和实际条件下的静止状态、运动状态的体间相对位置和姿态变化可以通过运算该4×4阶齐次方阵来实现，从而完整地描述出刀具的实际运动轨迹以及S型型面切削下的误差分布。即:

刀具成形点的成形函数:

位置误差:

姿态误差:

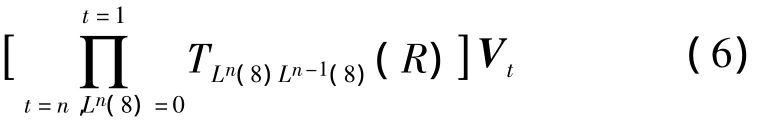
式中:方阵T为机床相邻部件的体间静止、运动特征矩阵;T（R）为体间静止、运动角误差特征矩阵;Pt为实际加工点在刀具坐标系中的齐次坐标;Pw为理想加工点在工件坐标系中的齐次坐标;Vw为实际加工中刀具姿态矢量在工件坐标系中的齐次坐标;Vt为理想加工中刀具姿态矢量在工件坐标系中的齐次坐标。

2 S型试件型面误差辨识研究

2．1 型面误差溯源算法

影响数控机床加工轮廓误差的动态因素很多，涉及到各轴的位置环、速度环、加速度、加加速度等。在辨识因素较多的情况下，直接利用神经网络建立辨识关系不仅耗时，而且识别准确率和精度很低。为此，利用计算模糊隶属度的方法首先溯源出影响机床性能的主要动态因素。针对S型试件误差分布结果，选择正态模糊隶属函数进行计算［7］，如式（7）所示。首先建立起每一个动态因素变动时对应的法向误差矩阵Ei=（ai1，ai2，…，ain）（Ei表示第i个动态因素对应的误差矩阵，n表示误差矩阵中包含的误差值个数）。然后基于误差矩阵与动态因素之间一一对应的映射关系，将实验切削误差X=（x1，x2，…，xn）代入式（7）计算出对于Ei的隶属度。

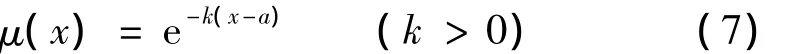
式中:a为Ei中的误差值;x为给定误差矩阵中的误差值;e为自然数函数，取2.718 28。

为了确定X与Ei的相似程度，将计算出的隶属度μB=（μ1，μ2，…，μn）代入绝对海明公式（8）中计算出对应的贴近度值，按照贴近度最大原则，最终溯源出影响机床动态性能的主要动态因素。

其中:μA（xi）=1。

2．2 基于神经网络训练的溯源因素解析

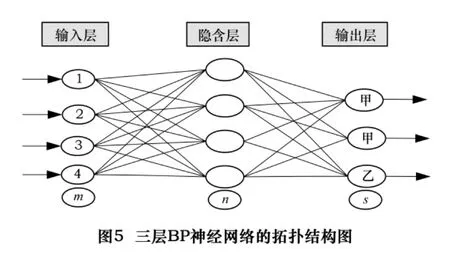
BP算法由数据流的前向计算和误差信号的反向传播2个过程构成［8］。三层BP神经网络的拓扑结构如图5所示，包括输入层、隐含层、输出层，各层分别有m、n、s个神经元。上一层的每个神经元与下一层的每个神经元形成全连接，连接强度用权值表示。通过误差的反向传播来逐层修正各连接权值，从而不断提升BP神经网络的准确度。

传递函数是BP神经网络的辨识精度和辨识效率重要影响因素之一，因此必须要选择符合网络的传递函数。BP网络的传递函数有多种，分别为Logsig型传递函数、tansig型传递函数以及purelin型传递函数。训练时分别选择上述3种类型的传递函数进行训练，在网络其他参数不变的情况下使用tansig函数时要比其他类型传递函数的误差小，所以选用的传递函数是tansig。

BP神经网络需要选择适合的隐含层单元数，单元数太少不能有效处理所面临的问题，单元数太多，不仅耗时而且还会出现过度吻合的现象致使达不到辨识要求。为此，采用了循环训练的方法，先使用较少的隐层节点数，再在循环训练中不断增加隐含层节点数，直到学习误差不再明显增加为止。

3 数控机床切削S型试件误差辨识计算实例

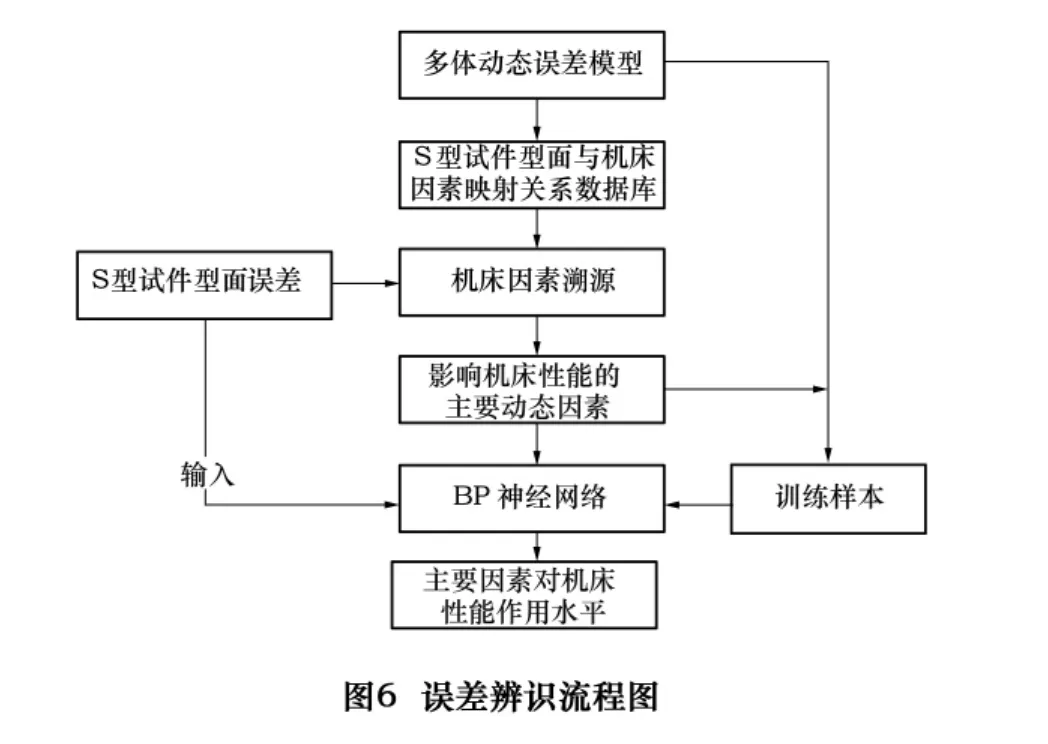
针对某国产数控机床进行切削实验，机床型号为V5－1030－ABJ，基于切削的S型试件形面误差进行误差溯源与误差辨识，计算过程如图6所示。

3．1 S型试件型面与机床因素映射关系数据库

通过第1．1、1．2节建立的多轴联动动态误差模型，可以计算出S型试件型面误差与机床因素间的映射关系，如图7所示。通过误差分析，初步筛选对机床动态性能造成明显影响的17个动态因素，如表1所示。每个因素考虑了两种工况，构成动态因素集为

表1 多因素对于各单因素的贴近度值表（X、Y、A、B分别代表各运动轴）

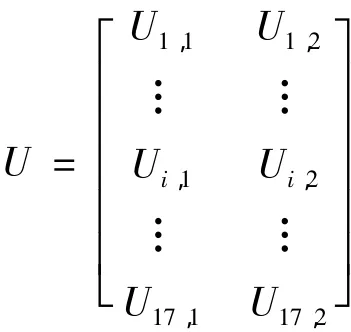
其中 Ui，1、Ui，2分别表示第 i个因素的第一工况和第二工况，与其对应的误差数据库为

3．2 机床因素溯源及水平提取

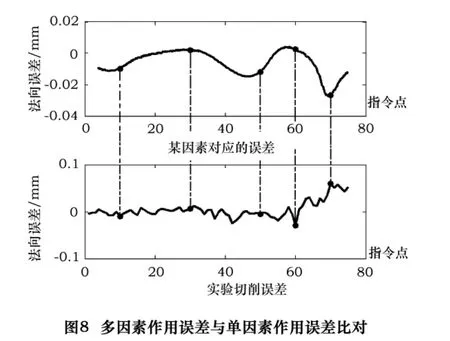
将实验切削误差 X=（x1，x2，…，xn）与机床因素映射关系数据库中的每一组Eij（j代表第j工况，j=1或者j=2）比对，如图8所示。按照式（8）计算出贴近度值，如表1所示。

分析表 1，依据贴近度最大的原则，U1，1，U5，2，U6，1是贴近度较大的三个动态因素，分别对应着机床的位置增益工况1，B轴加速度工况2，X轴加加速度工况1。说明了这三个动态因素是影响误差的主要动态因素，因素及工况溯源结果如表2所示。

3．4 BP神经网络误差因素解析

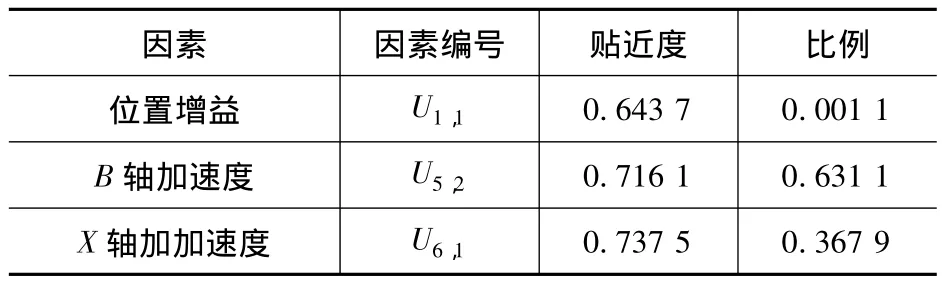
表2 提取因素及水平表

4 结语

提出了一种辨识机床动态性能影响因素的新方法。通过机床切削S型试件的型面误差分析，溯源出对机床加工影响较大的动态因素，最后利用BP神经网络对动态因素作用水平进行量化辨识。通过某国产机床切削实例分析，针对一组切削实验误差数据进行动态因素辨识，通过多体误差模型分析出对机床性能影响明显的17个动态因素，运用误差溯源模型再从中溯源出3个最主要动态因素，最终结合BP神经网络进一步确定了主要动态因素对机床性能的作用水平。该方法可用于机床动态性能的测评，提高机床加工性能和工件加工质量、加工效率，完善基于S型检验试件校验机床动态性能的测试方法。

［1］Lai J M，Liao J S，Cheng W H，et al．Modeling and analysis of nonlinear guide way for B measurement and diagnosis［J］．Int．J．Math．Tool．Manufacturing，1997，37（5）:687－707．

［2］范晋伟．基于多体系统运动学的数控机床运动建模及软件误差补偿技术的研究［D］．天津:天津大学，1996．

［3］赵小松，方沂，章青，等．四轴联动加工中心误差补偿技术的研究［J］．中国机械工程，2000，11（6）:637－639．

［4］Uddin S M，Ibaraki S，Matsubara A，et al．Prediction and compensation of machining geometric errors of five－axis machining centers with kinematic errors［J］．Precision Engineering，2009，33（4）:194－201．

［5］Tsutsumi M，Yumiza D，Utsumi K．Evaluation of synchronous motion in five－ axis machining canters with a tilting rotary table［J］．Journal of Advanced Mechanical Design，Systems and Manufacturing，2007，1（1）:24－35．

［6］李圣怡，戴一凡．精密和超精密机床精度建模技术［M］．长沙:国防科技大学出版社，2007．

［7］王季方，卢正鼎．模糊控制中隶属度函数的确定方法［J］．河南科学，2000，18（4）．

［8］葛哲学，孙志强．神经网络理论与MATLAB R2007实现［M］．北京:电子工业出版社，2009．