基于Kriging算法的海底地形插值设计与实现

申 静, 苏天赟, 王国宇, 刘海行, 李家钢

(1. 中国海洋大学 信息科学与工程学院, 山东 青岛 266100; 2. 国家海洋局 第一海洋研究所, 山东 青岛266061; 3. 中海石油研究总院, 北京 100027)

基于Kriging算法的海底地形插值设计与实现

申 静1, 苏天赟2, 王国宇1, 刘海行2, 李家钢3

(1. 中国海洋大学 信息科学与工程学院, 山东 青岛 266100; 2. 国家海洋局 第一海洋研究所, 山东 青岛266061; 3. 中海石油研究总院, 北京 100027)

针对目前海底地形构建方面存在的问题与不足, 基于普通Kriging的计算公式, 以渤海海域采集的离散高程点数据为例, 对构建海底地形高程模型的空间插值方法——Kriging方法进行了研究。针对海底地形建模的具体实现, 重点对Kriging算法的数据分布检验、数据分组、球形模型拟合、网格化插值以及结果显示等模块进行研究。最后, 基于Visual C++ 6.0平台对海底地形高程的插值过程进行了编程实现和可视化表达, 从而成功构建出渤海局部海域的海底地形特征, 为海洋科学研究和工程建设提供了参考和依据。

Kriging; 插值; 地形; Visual C++; 可视化

构建高精度的海底地形高程模型是海洋科学研究和工程开发的基础。由于海洋特殊的地理环境, 海底地形数据的获取需要耗费大量的人力和物力, 人们只能获得有关海底地形的部分离散水深数据。因此, 需要借助合适的插值算法, 基于采集到的离散水深点数据, 构建出合理的海底地形高程模型, 为海洋科学研究和工程开发提供基础数据。

Kriging插值法, 又称空间局部估计或空间局部插值法, 是地统计学的主要内容之一。它是以南非矿业工程师 D.G.Krige(Kriging)名字命名的一项实用空间估计技术, 目前已被广泛应用于矿产储量计算、遥感数据处理、地质学、水文学、环境科学、农林科学和农田水利等诸多方面。其插值实质是利用区域化变量的原始数据和变异函数的结构特点, 对未采样点的区域化变量的取值进行线性无偏、最优估计。与传统插值方法相比它具有两个明显优势[1]: (1)在数据网格化过程中考虑了被描述对象的空间相关性,使估计结果更科学、更接近实际情况; (2)给出了估计误差, 使估值精度更明了。

本文主要尝试将Kriging插值方法应用到海底地形高程模型的构建中, 实现海底地形高程的合理插值与可视化。

1 Kriging插值原理

1.1 插值条件和变异函数

在研究区域内, Kriging方法将所研究的对象称为区域化变量(如孔隙度、渗透率等), 区域化变量具有两个最显著的特征, 即随机性和结构性[2-3]。用Kriging方法进行插值时, 一般需要区域化变量 z(x)满足二阶平稳假设或区域化变量 z(x)的增量[z(x) - z (x + h )]满足本征假设[4], 即: (1)在整个研究区域内, 区域化变量 z(x)的增量[z(x) - z (x + h )]的数学期望为 0, 即 E (z(x)- z(x +h)]=0, ∀x, ∀h; (2)在整个研究区域内, 增量[z(x) - z (x + h )]的方差函数存在且平稳(不依赖于 x), 即Var[z(x) - z (x + h )]=E[z(x) - z(x + h ) ]2=2γ(h),∀x, ∀h

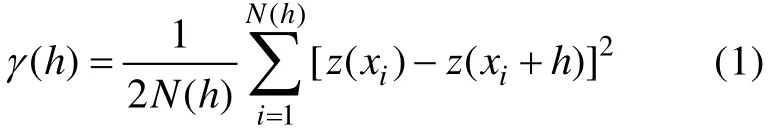
式中γ(h)称为变差函数或变异函数(variogram),因为它为方差的一半, 所以有时又称半变差函数或半变异函数(semivariogram), 它是地统计分析所特有的基本工具。h为两样本点空间分隔距离,z(xi)和z(xi+ h )分别是区域化变量 z(x)在空间位置 xi和xi+ h 处的实测值, N(h)表示距离为 h时数据点对的数目。由变异函数公式可以进一步推出如下关系式:

1.2 Kriging方程组

设z(x)是点x的区域化变量, 且满足二阶平稳(或本征假设)。假设在点x的临域内共有n个实测点, 即x1,x2,… ,xn, 其样本值为z(xi)[i= 1 ,2,… ,n]。那么,普通Kriging法的插值公式为:

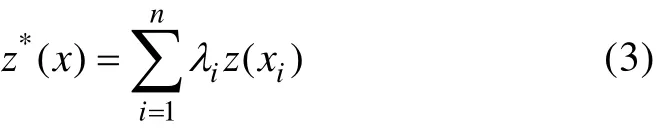
z*(x)表示区域化变量z(x)的无偏最优估计量,λi为权重系数, 表示各空间样本点xi处的观测值z(xi)对估计值z*(x)的贡献程度。普通Kriging方程组为:

写成矩阵的形式为:AB=λ

由 Kriging的求解过程可知, 协方差矩阵(变异函数) 对于Kriging插值的影响较大, 估计变异函数是一个较为复杂的过程[5], 也是 Kriging内插的第一步。由于区域化变量的变异函数不依赖于位置x, 所以为了预测, 在实际计算中常需要用理论变异函数模型来替代实验变异函数[6]。 Kriging法常用的理论变异函数模型有球形模型、指数模型、高斯模型、幂函数模型等, 其中球形模型是地统计分析中应用最广泛的理论模型[3], 公式如(5)。

2 海底地形插值与可视化设计

Kriging插值算法适用于存在空间相关性的区域化变量, 海底地形符合随机性和结构性的特征[7], 因此本文采用普通Kriging法对海底地形进行插值, 计算过程中认为海底地形的变化为“各向同性”, 并且采用 Visual C++对海底地形插值算法进行编程实现和可视化表达。在VC编程过程中, 为了便于程序的编写和维护, 需要对算法进行模块化分解, 然后对各模块进行单独编程和测试。程序处理流程如图 1所示。

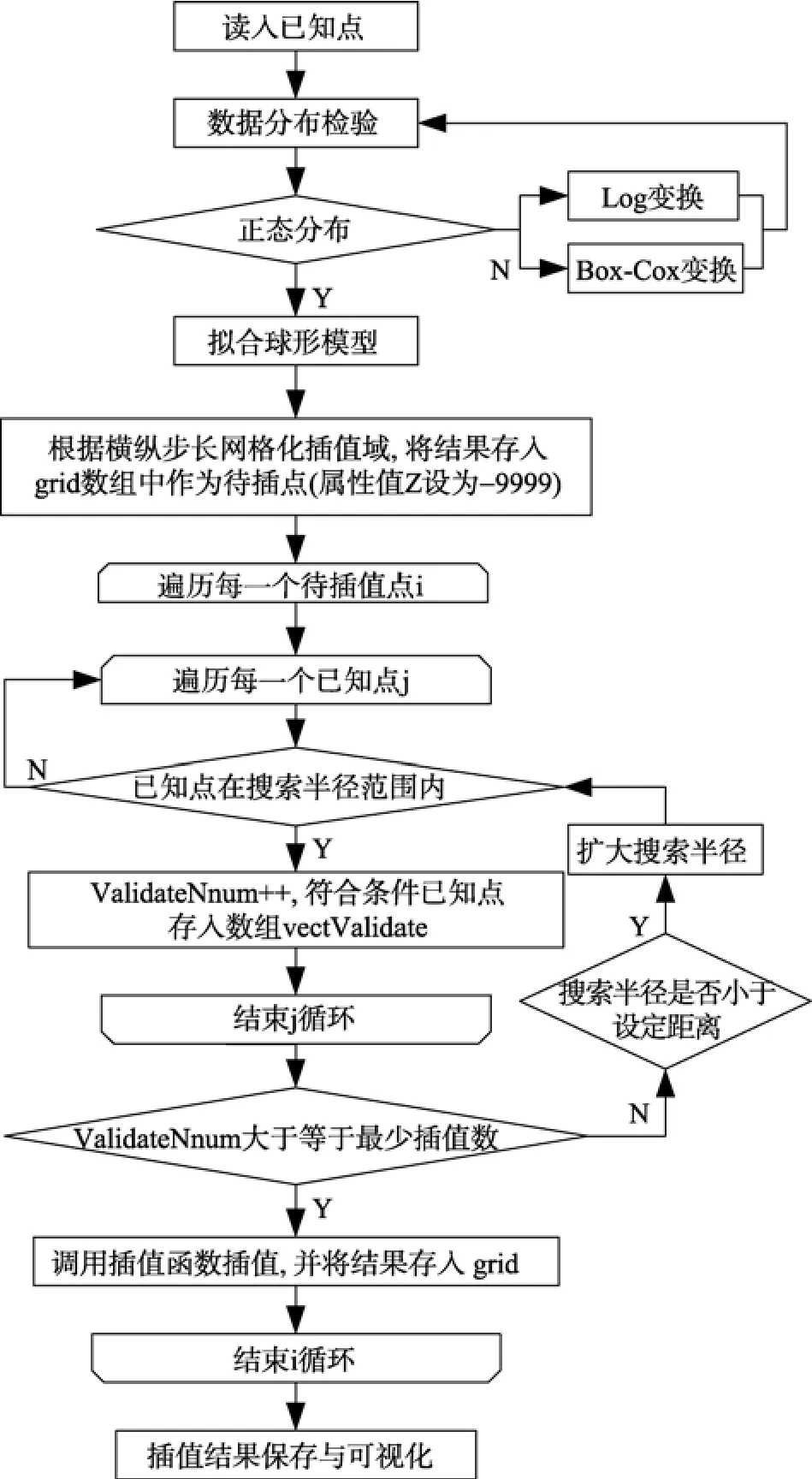
图1 编程流程Fig. 1 Program flow chart

2.1 文件数据的读取模块

开发读取文件函数 InputReader::Read(string filename, int mode)完成数据的读操作, mode控制读入数据的维数。本文通过建立可变长的矢量三维数组vectorm_input来存放数据的X,Y坐标和属性值Z。vector为C++标准模板类和函数库, 它能够存放任意类型的动态数组。

2.2 数据分布检验

Kriging插值算法(如普通Kriging、简单Kriging和泛 Kriging等)应用的前提是假设数据服从正态分布。因此, 在进行分析前, 检验数据分布特征, 了解和认识数据具有非常重要的意义。若不符合正态分布的假设, 应对数据进行变换, 使其转为符合正态分布的形式, 常用的变换有 Log变换和 Box-cox变换。数据的检验可以通过直方图完成。直方图指对采样数据按一定的分级方案(如等间隔分级)进行分级, 统计采样点落入各个级别中的个数或占总采样数的百分比, 并通过条带图或柱状图表现出来。

2.3 数据分组

2.4 拟合球形模型模块

开发 GetSphericalModel(const ForwardIterator start,int Size)函数拟合球形模型。由公式(5)可知当。如果记x= h3, 则可以得到线性模型:2

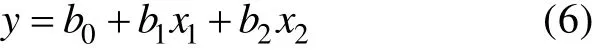
根据参数 b0,b1, b2的定义, b0＞ 0 ,b1＞ 0,b2＜0。可是在对模型(6)的拟合过程中, 可能会出现参数符号不符合要求的情况, 从而无法正确地求出球形模型参数c0，c和a。因此, 本文针对拟合结果中b0,b1,b2系数符号不符合要求的情况做了详细的分析处理:

(2)b0＜ 0 时, 令 b0= 0 , 解 yi= b1x1i+ b2x2i,

若求出 b1＞0,b2＜0, 则可得到球形模型参数;

若求出 b1＞0,b2＞0, 则令b2=0, 重新解yi= b1x1i,若求出 b1＞ 0 则可完成拟合, 否则拟合不成功。

(3)当 b0≥ 0 ,b1＞0, 但 b2≥ 0 时, 令 b2= 0 , 解yi= b0+ b1x1i,

综上所述，随着教育改革的不断发展，要清楚认识到学生才是课堂中的主体。在教学中要从以学生为主体入手，运用互动教学法来激发出学生的学习主动性，培养好学生的学习能力，在促进学生思维发展的基础上来提高语文教学质量。

若求出 b0＞0,b1＞0, 则可得球形模型参数;

若b0＜0,b1＞0, 则令b0=0, 重新解yi= b1x1i。

若求出 b1＞ 0 , 同样可以完成拟合, 否则拟合不成功。

程序针对拟合不成功的情况下, 统一采用yi= x1i的线性拟合。

2.5 Kriging插值模块

2.5.1 网格化

由于读入的数据为散乱点, 需要对其进行规则化处理, 根据读入海底数据的横纵坐标的最大值、最小值和用户设置的横纵坐标步长即网格化的横纵坐标间隔将散乱点网格化, 并将得到的坐标值 X,Y存入三维矢量网格数组 grid中。为了统一识别无效网格点, 每一个网格点 grid的属性值 Z的初始值设为–9999。

2.5.2 确定已知插值点

对于预测点, 每个输入点都有着局部影响, 这种影响随着距离的增加而减弱。所以在进行模型拟合时, 可以利用预测点临近的已知点进行拟合, 根据需要, 设置搜索半径和插值所需的最少已知点个数。如果搜索半径范围内已知点的个数少于待插值点所需的个数时, 可以扩大搜索半径, 继续搜索。

2.5.3 插值计算

由拟合球形模型模块可知, 求变异函数时, 只要求出参与插值的两已知点的距离和待插点与已知点间的距离就能求出矩阵 A和B。另外在求解权重系数公式(4)时, 本文用到了矩阵的LU分解法[8]来加快矩阵的求解速度。权重系数求解完毕后, 带入普通Kriging的求解公式(3)中完成海底地形高程的插值,将结果存入grid数组中将grid默认的–9999更改为实际的插值结果。

2.5.4 交叉验证

为了验证插值结果的误差, 可以利用交叉验证法[9](对数据集中任何一个样本i( i=1, 2, …, n; n为样本总数), 由其余n－1个样本的观测值对该样本作出的估计值来评价预测精度), 验证参数的合理性, 并进行相应的调整。

2.6 插值结果显示模块

开发位图 DIB类, 根据插值得到的高程值数组grid中的属性值的最大值和最小值, 设置调色板的色阶分类和对应的属性值区间。对每一个网格的属性值, 可以从调色板中获得对应的RGB颜色索引值,进而对该网格进行渲染。遍历每一个网格进行绘制,即可得到直观表达海底地形特征的可视化图件。

3 海底地形插值应用实例

本文以实测水深数据为例, 基于设计的 Kriging地形插值算法, 对渤海局部海域的海底地形进行插值计算和可视化。

在计算过程中, 本文首先对实测数据进行了平稳假设验证。通过对数据直方图(图2)进行分析, 发现统计量偏度接近于0, 峰度接近于3, 均值与中值相近, 直方图中柱状呈对称分布, 类似于一个倒扣的钟, 数据近似于正态分布, 可以进行 Kriging插值。

图 3给出了数据分组后拟合球形模型的参数(a= 6 6395.380,c0= 6 .421,c= 1 4.683)从图中可以看出, 随着距离的不断增大, 变异函数的不断递增, 当增加到变程a时, 变异函数趋于平稳。

图2 水深数据分布直方图Fig. 2 Distribution of water depths

图3 交叉验证图Fig. 3 Cross-examination

分析交叉验证图(图 4), 发现预测误差相对较大的数值主要分布在与周围实测值属性值变化较大的点上, 也就验证了Kriging插值法的实质是一个局部估计的加权平均, 具有一定的平滑作用, 尤其可以平滑掉一些极端值[10]。从图5插值结果可以看出, 本文采用的Kriging方法能够比较客观、真实地反映海底地形起伏特征。

图4 拟合球形模型图Fig. 4 Spherical modeling

图5 渤海局部水深地形Fig. 5 Local water depth terrain of the Bohai Sea

4 结语

通过算法设计、开发和应用实践, 本文设计的Kriging插值程序能够真实地反映出空间对象的变化特征。但相对于其他插值方法(如距离反比加权法) ,Kriging法复杂得多,需要根据具体的插值对象设置变异函数的参数和距离h的分类, 计算步骤繁琐, 影响了插值速度。文章进行 Kriging算法编程过程中,对算法进行了优化, 计算效率得到了提高。但是程序对插值点数进行限制是以牺牲精度来提高效率, 并且当处理的数据量比较大时, 容易出现内存溢出和运算效率降低的现象, 今后需要重点研究和解决Kriging算法在这方面存在的问题。

[1] 包世泰, 廖衍旋, 胡月明, 等. 基于 Kriging的地形高程插值[J]. 地理与地理信息科学, 2007, 23(3):28-32.

[2] 赵俊兰. Kriging法在GIS空间数据内插中的应用[J].有色金属(矿山部分), 1998, 3: 35-38.

[3] 李晓军, 王长虹, 朱合华. Kriging 插值方法在地层模型生成中的应用[J]. 岩土力学, 2009, 30(1):157-162.

[4] 王靖波, 潘懋, 张绪定. 基于 Kriging方法的空间散乱点插值[J]. 计算机辅助设计与图形学学报, 1999,11(6): 525-529.

[5] 颜辉武, 祝国瑞, 徐智勇, 等. 基于 Kriging 水文地质层的三维建模与体视化[J]. 武汉大学学报(信息科学版), 2004, 29(7): 611-614.

[6] 鲜乾坤, 万宁, 贺全兵, 等. 基于 Kriging插值的 3D地形可视化[J]. 四川理工学院学报(自然科学版),2009, 22(6): 47-53.

[7] 李国敏, 陈崇希. 克立格法在地下水数值模型中的应用[J]. 地质科技情报, 1995, 14(3): 95-99.

[8] 纪坤, 陈建平. LU分解分块算法的研究与实现[J].南京师大学报(自然科学版), 2008, 31(计算机专辑):55-60.

[9] 吴学文, 晏路明. 普通 Kriging 法的参数设置及变异函数模型选择方法——以福建省一月均温空间内插为例[J]. 地球信息科学2007, 9(3): 104-108.

[10] 尉英华, 郭品文, 刘洪滨. 利用插值法建立历史旱涝格点资料的可行性[J]. 气象与减灾研究, 2007, 30(3):1-6.

Submarine topography visualization based on Kriging algorithm

SHEN Jing1, SU Tian-yun2, WANG Guo-yu1, LIU Hai-xing2, LI Jia-gang3
(1. Ocean University of China, the College of Information Science and Engineering, Qingdao 266100, China;2. First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China; 3. Petroleum Research Institute, Beijing 100027, China)

Oct.,24,2011

Kriging; interpolation; topography; Visual C++; visualization

On the basis of Kriging interpolation algorithm, we constructed the sea floor elevation model using discrete bathymetry points. In the model constructing, key modules including normal distribution verification, data binning, spherical model fitting, grid interpolation and grid visualization were designed. The visualization program and key modules were developed on the Visual C++ 6.0 platform. Part of the Bohai Sea elevation model was constructed using discrete bathymetry survey points.

P208; TP391

A

1000-3096(2012)05-0024-05

2011-10-24;

2012-03-06

“十二五”国家科技重大专项子任务(2011ZX05056-001-01)

申静(1987-), 女, 山东潍坊人, 中国海洋大学在读研究生,E-mail: shenjingshenwei@163.com

(本文编辑：刘珊珊)