流线型宽顶堰的流量系数和淹没系数
王学斌,张毅
(中国水电建设集团第十五工程局有限公司,陕西西安 710065)
1 流线型宽顶堰的研究现状
宽顶堰广泛的应用于各种进水闸、无压隧洞、涵洞的进口、桥孔、施工围堰等。宽顶堰分为直角型宽顶堰和流线型宽顶堰。直角型宽顶堰的进口为直角;而流线型宽顶堰的进口为圆形或流线型。虽然只是堰的进口稍有差别,但流线型宽顶堰的泄流能力却比直角形宽顶堰的泄流能力大许多。
前苏联的伯朗日、巴赫米切夫、彼卡洛夫、A·P·别列津斯基都通过试验研究了宽顶堰的流量系数[1],尤其是A·P·别列津斯基,对宽顶堰的流量系数做了系统的试验,给出了堰前为直角形和圆形的流量系数的计算方法[2],此方法一直为我国水力学教学所用。研究表明,直角形宽顶堰由于堰顶处水流分离,不能用理论方法得出流量系数的公式,但对于流线型宽顶堰,流量系数可以用边界层理论进行分析[3]。
宽顶堰分为自由出流和淹没出流,自由出流的流量计算比较简单。对于淹没出流,计算流量时须同时考虑流量系数和淹没系数。对于淹没系数,A·P·别列津斯基给出了试验成果,这一成果是以表格形式给出的,没有计算公式。近年来,有的学者对宽顶堰的淹没出流进行过研究,文献[4]采用临界淹没法计算宽顶堰的流量,所谓临界淹没法是指宽顶堰刚刚开始处于淹没状态的情况。文献[5]研究了淹没宽顶堰的泄流能力,认为宽顶堰的淹没系数不仅与流量系数有关,而且与侧收缩系数有关,给出了侧收缩系数为1.0、0.95和0.9情况下不同流量系数时淹没系数的计算表,但该计算方法未得到试验的证实。
本文主要根据边界层理论研究流线型宽顶堰的流量系数,得出宽顶堰流量系数的理论计算方法。至于淹没系数,则根据A·P·别列津斯基给出的表格,提出淹没系数的计算公式。
2 流线型宽顶堰的流量系数
流线型宽顶堰如图1所示。设堰上水头为H,行近流速为v0,堰高为P,堰长为L,根据边界层理论,当水流通过流线型宽顶堰时,在堰顶附近形成边界层,边界层的厚度为δ。假设堰顶上的临界水深hk位于堰顶下游端附近,该断面的水压力呈静水压力分布,边界层厚度与水深相比较是很小的,边界层以外的水流流速分布是均匀的。
根据以上假设,由伯努利方程求出边界层以外的势流流速U0为
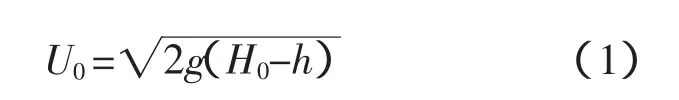
式中,U0为堰顶以上总水头;g为重力加速度;h为堰顶水深。用势流流速与边界层位移厚度表示的流量公式为[6]

式中,A=bh为过水断面面积;x=b+2h为湿周;δ1为边界层的位移厚度。将式(1)代入式(2)得

由临界水深理论可知,能使流量为最大的水流条件即为临界水深条件,对上式求微分并令dQ/dh=0,可得临界水深公式为

图1 流线型宽顶堰简图Fig.1 Sketch of streamlined broad crest weir
将上式代入式(3)得

一般流量公式为

比较公式(5)和(6)得流量系数为

式(7)即为流线型宽顶堰流量系数的计算公式。由上式可以看出,宽顶堰的宽度、堰顶以上总水头确定以后,流线型宽顶堰的流量系数决定于边界层的位移厚度δ1。
流线型宽顶堰顶边界层的发展可视为平板边界层的发展。对于平板流速分布规律可以用对数律表示为
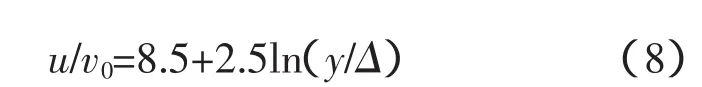
式中,u为边界层内的流速;v0为摩阻流速;y为边界层内任一点距壁面的距离;Δ为绝对粗糙度。当y=δ时,u=U0,上式变为

壁面切应力系数为


文献[7]给出了平板的壁面切应力为

令公式(10)和(11)相等,得边界层的厚度为

边界层的位移厚度用下式计算

将公式(8)和公式(9)代入积分得

将公式(12)代入公式(14)得

将公式(15)代入公式(7)即可求得流量系数。
3 宽顶堰的淹没系数
A·P·别列津斯基给出的宽顶堰的淹没系数如表1所示,表中σ为淹没系数,hs为从堰顶算起的下游水深,H为堰上水深。
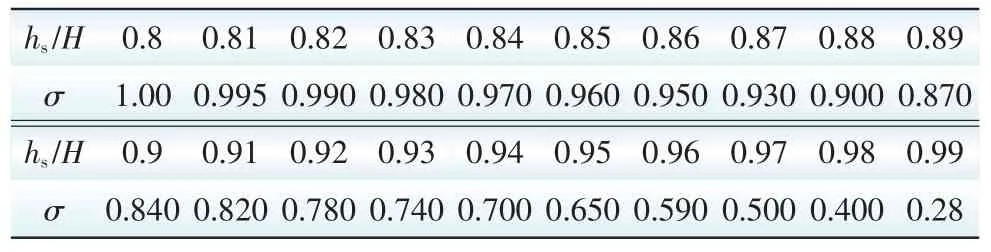
表1 A·P·别列津斯基的宽顶堰淹没系数Tab.1 Submerged coefficient of broad crest weir given by A·P·Березинский
表中的数据查算比较麻烦,现根据表中的数据,对淹没系数拟合方程为

图2是公式(16)计算值与表中数据的对比,可以看出,曲线吻合良好,除hs/H=0.96时误差为4.67%和hs/H=0.99时误差为5.4%外,其余误差均小于3%。

图2 淹没系数σ与hs/H关系Fig.2 Relationship between σ and hs/H
4 算例
某进水闸,共三孔,每孔净宽b=5.0 m,底坎高P=0.5 m,堰的前缘为圆头形,堰长L=12 m,闸墩采用半圆形,边墩采用圆弧形。当闸门全开时,堰顶水头H=2.0 m,闸前行近流速v0=0.6 m/s,堰表面的粗糙度Δ=0.6 mm,闸墩系数ξ0=0.45,边墩系数ξK=0.7,求自由过闸的流量。如果下游水深超过堰顶的高度为1.85 m,试求淹没出流时的流量。
解:
1)计算堰前总水头H0

2)计算侧收缩系数
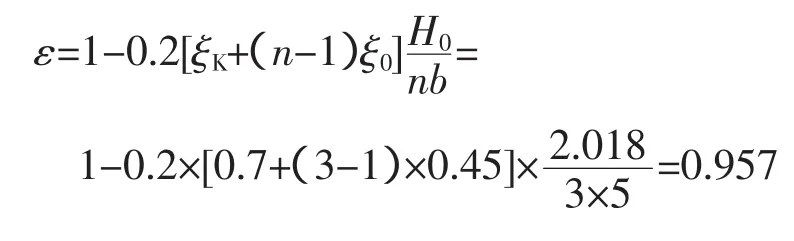
3)计算边界层的位移厚度δ1
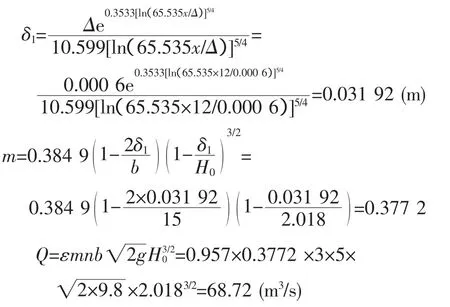
用A·P·别列津斯基的经验公式计算

两种计算方法相差了0.073%。
宽顶堰淹没出流的堰顶以上水深hs=1.85 m,hs/H=1.85/2=0.925,由公式(16)求淹没系数

由表1查得σ=0.76,Qσ=σQ=0.76×68.72=52.227 m3/s。用公式计算与用查表计算相差0.65%。
5 结语
本文根据边界层理论和前人对平板壁面阻力的研究成果,得到了边界层位移厚度的计算方法,提出了用边界层的位移厚度表示的流量系数的计算公式,利用A·P·别列津斯基对宽顶堰淹没系数的试验资料,拟合出了淹没系数的计算方法。通过算例和与经验公式以及查表法对比,验证了本文公式的正确性。
[1] И.И.Агроскин.水力学[M].清华大学水力学教研组,天津大学水利系水力学教研室译.北京:商务印书馆,1954:55-565.
[2] 吴持恭.水力学[M].2版.北京:高等教育出版社,1998:392-403.
[3]P·阿克尔斯,等.测流堰槽[M].北京市水利科学研究所译.北京:北京市水利科技情报站,1984:113-126.
[4]禹华谦.用临界淹没法计算宽顶堰流[J].重庆交通学院学报,1998,17(1):28-30.YU Hua-qian.Critical submerged method applied to the computation of flow over broad-crested weirs[J].Journal of Chongqing Jiaotong University,1998,17(1):28-30(in Chinese).
[5]华子平.对淹没宽顶堰泄流能力计算公式的探讨[J].河海大学学报,1998,26(3):97-101.HUA Zi-ping.A calculating formula for spillway capacity of drowned wide-crest weirs[J].Journal of Hohai University,1998,26(3):97-101(in Chinese).
[6] 张志昌,肖宏武,毛兆民.明渠测流的理论和方法[M].西安:陕西人民出版社,2004:111-119.
[7] 清华大学水力学教研组.水力学[M].北京:高等教育出版社,1983:309-312.
[8] 张志昌.水力学:下册[M].北京:中国水利水电出版社,2011:155-156.

