模糊自适应PI控制在直流无刷电动机调速系统的应用*

胡发焕 唐 军 邱小童

（①江西理工大学机电工程学院，江西赣州341000;②江西理工大学应用科学学院，江西赣州 341000）

目前直流无刷电动机（BLDCM）广泛应用于航空航天、军事、工业、医疗机械等诸多领域。BLDCM是一个多变量、强耦合、非线性、时变的复杂系统［1］，当系统负载或参数发生变化时，传统的PID控制将难以达到设计的预期效果。对这类高度非线性的系统，采用智能控制方法可获得更理想的效果，它具有提高系统的响应速度、稳定性和鲁棒性的能力。模糊控制是智能控制中最常用的方法之一，它不依赖于控制系统的精确数学模型，且对系统参数的变化不敏感，具有快速性及鲁棒性强的特点，适合BLDCM控制系统的要求。本文即采用应模糊自适PI控制的模式实现对BLDCM的控制。

1 工作原理及数学模型

直流无刷电动机主要由电动机本体和转子位置传感器两部分组成。在电动机本体上安装1台同步电动机，转轴上装有转子位置监测器，以测量转子磁极与旋转磁场的相对位置，为驱动电路提供参照信号。无刷电动机为了实现无刷换相，把直流电动机的电枢绕组放在定子上，把永磁钢放在转子上，这与传统直流永磁电动机的结构正好相反。由位置传感器、逻辑控制电路及功率开关电路共同组成换相装置，使直流无刷电动机在运行过程中，由定子绕组所产生的磁场与转子自身的永久磁场在空间始终保持约120°的电角度，从而产生磁转矩推动转子旋转。现以二相导通星形三相六状态无刷电动机为例，分析无刷直流电动机的数学模型［2］。三相绕组的电压平衡方程为:

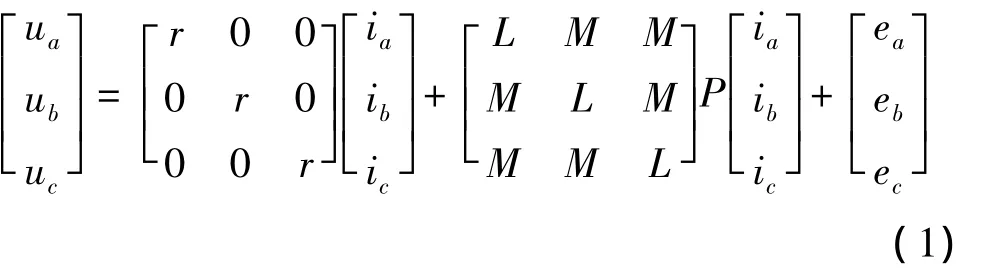
式中:ua，ub，uc为定子相绕组电压;ia，ib，ic为定子相绕组电流;ea，eb，ec为定子相绕组电动势;L为各相绕组的自感量;M为两绕组间的互感量;P为微分算子d/dt。因电动机为星形连接且无中线，则有:

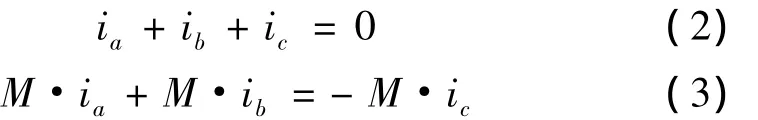
定子绕组产生的电磁转矩方程为

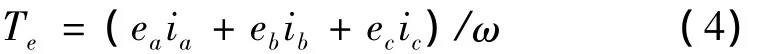
则电动机的驱动方程为

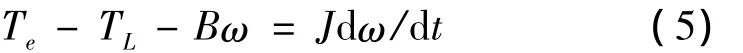
其中:Te为电磁转矩;TL为负载转矩;B为阻尼系数;ω电动机的角速度;J电动机转动惯量。

2 模糊自适应PI控制系统的设计

在电动机调速系统中，使用传统的PID控制器，可以得到较好的动态性能。但电动机是主要的谐波源之一，在运行时会产生大量的电磁干扰，引入微分环节在改善控制器动态性能的同时，也会对噪声信号进行放大，所以不合适的微分系数会使控制系统的稳态性能变差［3］，通常使用 PI控制器就能满足系统的性能要求，鉴于这个原因，本文设计的速度控制器不引入微分，而采用PI控制器。BLDCM是一个多变量、强耦合、非线性的复杂系统，当系统负载或参数发生变化时，要达到满意的控制效果则必须实时改变PI控制参数，因此，传统的PI控制器将难以达到满意的效果。对这类高度非线性的系统，采用智能控制方法则可获得理想的效果，它具有提高系统响应速度、稳定性和鲁棒性的能力。模糊控制是智能控制中常用的方法之一，它具有不依赖于控制系统的精确数学模型，对系统参数的变化不敏感，具有快速性及鲁棒性强的特点，很适合BLDCM控制系统的要求。本文即采用模糊自适应PI对其进行速度控制。在直流无刷电动机控制系统设计中，本文采用双闭环控制:速度环和电流环。在电流环控制器中，采用传统的PID控制即能达到满意的效果;为了提高系统的响应速度和改善控制效果，对速度环采用基于模糊控制理论的模糊自适应PI控制，其系统框图如图1所示。

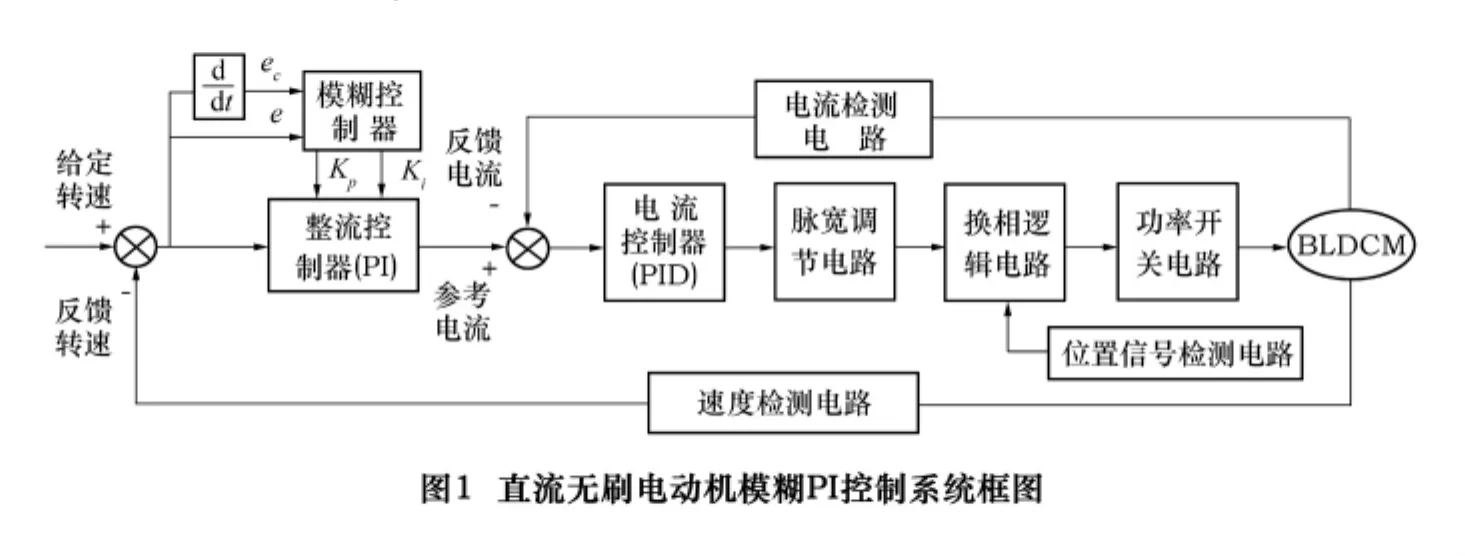
3 模糊控制器的设计

模糊控制器由模糊规则库、模糊推理机、模糊化接口和解模糊化接口4部分组成。本文设计的模糊控制器是双输入、双输出模式，其构成如图2所示。其输入为电动机的转速偏差e和转速偏差变化率ec，输出为参数Kp、Ki。模糊控制器的输入量偏差e和偏差变率ec必须经模糊化后，才能成为模糊推理机的输入量。模糊推理机根据模糊关系推理合成规则［4］Uij=（Ei×ECj）·R计算出输出量，输出量Uij仍为模糊变量，要经过解模糊化后才是模糊控制器的实际输出量Kp和Ki，它们用于实时调节速度PI控制器的比例增益系数Kp和积分增益系数Ki。

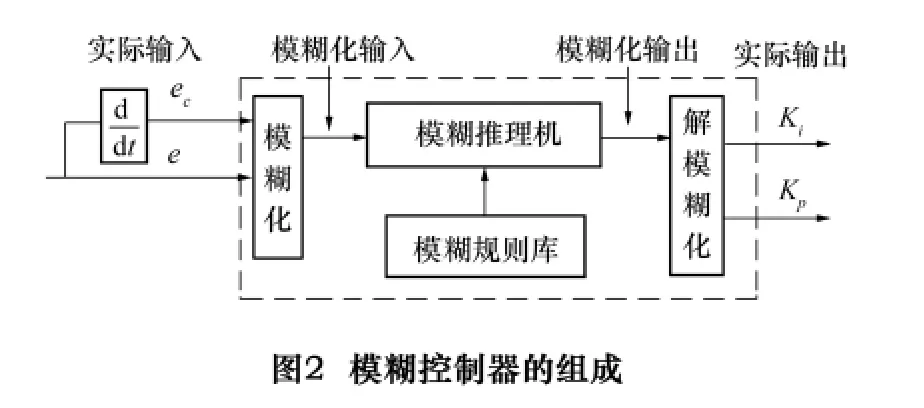
3.1 确定输入、输出变量的变化范围和量化因子

本文的控制对象为maxon公司生产的EC45无刷电动机，其基本参数是:额定电压36 V，额定电流5.24 A，额定功率150 W，额定转速4 200 r/min，相电感0.26 mH，相电阻2.47 Ω，机械时间常数7.44 ms，转子惯量119 g·cm2。本文设计的模糊控制器输入、输出变量论域均设为［－6，6］，用7个语言变量{NL，NM，NS，ZO，PS，PM，PL}表示。隶属度函数均采用三角形隶属度函数，如图3所示。

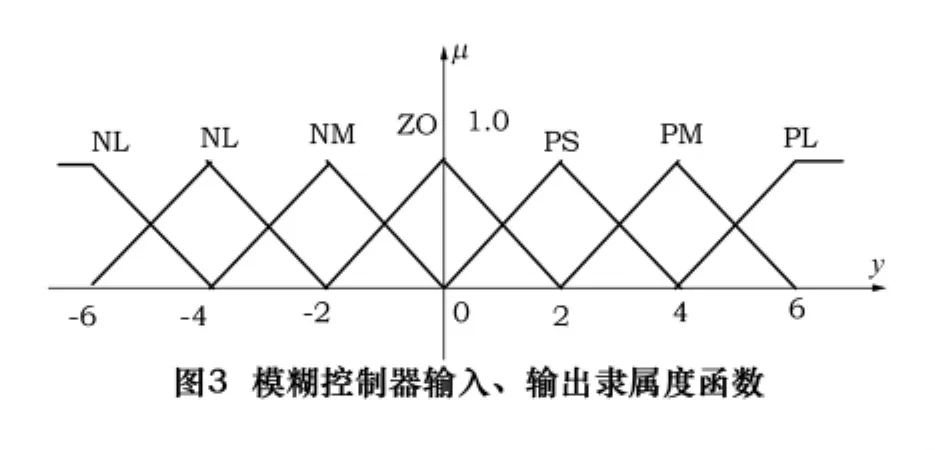
根据专家经验，系统转速偏差e（t）=r（t）－c（t）（其中r（t）为目标转速，c（t）为实际转速）达到60 r/min时，就应该是语言值的“PL”，即60×Ke=6，则偏差的量化因子Ke取0.1。对于偏差变化率有:de（t）/dt=dr（t）/dt－ dc（t）/dt，因为 dr（t）/dt=0，所以 de（t）/dt=dc（t）/dt，根据电动机的机械时间常数和专家经验，偏差变化率为80 r/min/s时就应对应语言的“PL”，即80×Kc=6，所以偏差变化率的量化因子Kc取0.075。对输出变量Kp和Ki确定本文采用“1/4衰减”法来确定其“PL”。根据专家调试经验，先设Ki=0，从小到大调节Kp，当系统出现等幅振荡时，记下此时的值Ku，则0.65 ×Ku即为Kp语言值的“PL”。确定Kp后，先使Kp=“PL”，然后从小到大调节Ki，当系统出现等幅振荡时，记下此时的值Kv，则0.6×Ku即为Ki的语言值的“PL”。进过多次实验取得，本文Kp的“PL”对应值为2.2，即2.2 ×Kpp=6，则Kp量化因子Kpp取值2.73;Ki的“PL”对应值为 0.46，即0.46×Kii=6，则Ki量化因子Kii取值13。

3.2 设计模糊推理规则

模糊推理规则是模糊控制器的关键，其控制规则是建立在长期的控制经验、专家知识和仿真的基础之上的。通过模糊推理，得到模糊输出即模糊解，本文模糊控制器的输出形式采用增量式输出。进行模糊推理，要遵守一定的模糊规则，本文的控制对象是直流无刷电动机，应服从如下规则［4］。

（1）当偏差|e|=L时，取较大的Kp，而Ki=0;

（2）当偏差|e|=M且变化率|ec|=L时，应取较小的Kp和中等的Ki;

（3）当偏差|e|=M且变化率|ec|=S时，应取较小的Kp和较小的Ki;

（4）当偏差|e|=S时，应取较大的Kp和Ki。

在上述规则的条件下，根据专家知识和工程师的经验，本文制定出模糊规则表，如表1、表2所示。

3.3 解模糊化过程

表1 Kp参数模糊规则表

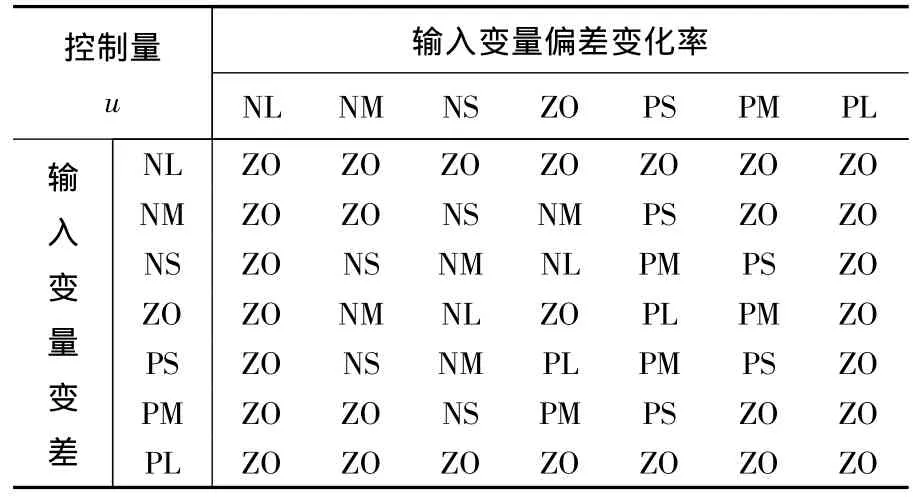
表2 Ki参数模糊规则表

偏差和偏差变化率通过各自的量化因子转化为论域中的元素，即完成输入变量的模糊化。通过模糊推理机，得到模糊输出变量，但这个输出量必须经过解模糊化后才能作用于控制对象。解模糊化有多种方法，常用的方法有最大隶属度法、加权平均法、重心法，其中最合理的是重心法，但重心法的计算量较大。由于本文输入、输出变量的模糊等级不多，计算量不大，故本文的解模糊化采用重心法来实现。重心法是取模糊隶属度曲线与横坐标所围成面积的重心为模糊推理的最终输出值。即

对于n个输出量化级数的离散论域则为

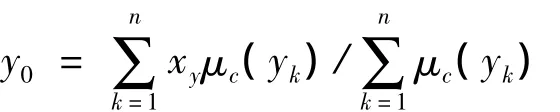
经过解模糊化后，模糊控制器输出具体的Kp、Ki值给速度控制器，速度控制器是一个PI控制器，模糊控制器就是根据负载和参数的具体变化实时地调整速度PI控制器的Kp、Ki参数值，使系统分工作于最佳状态。

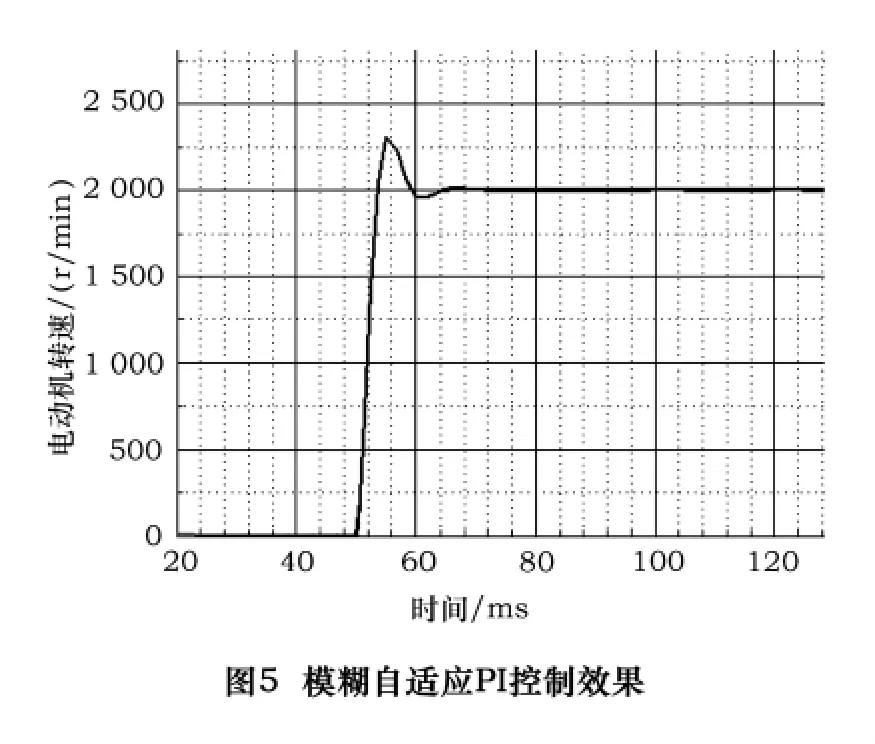
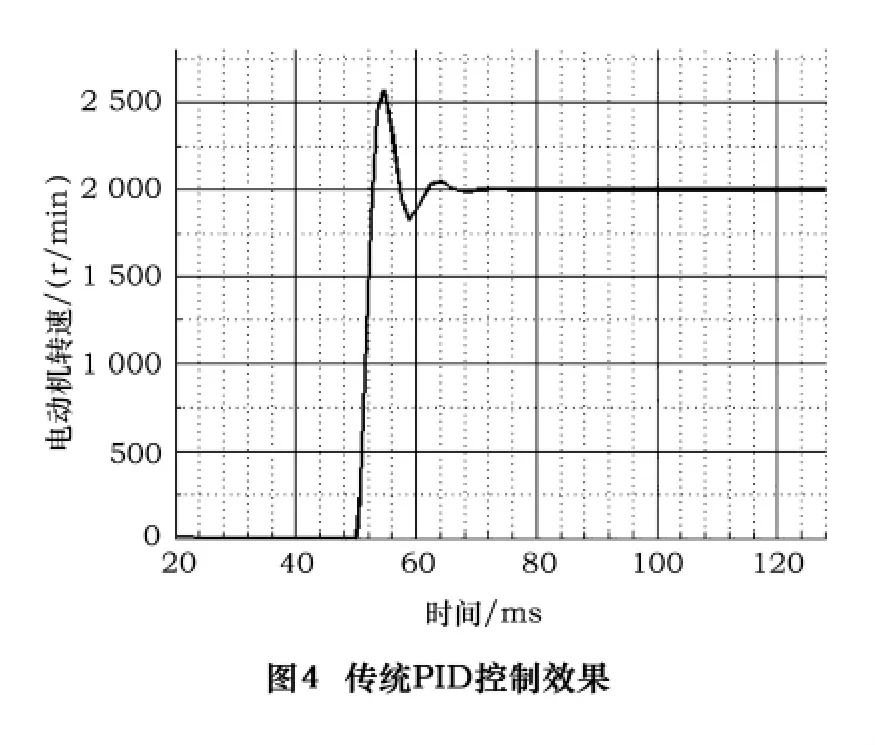
4 实验结果

笔者通过实验把基于模糊自适应PI控制的结果与传统的PID控制器进行比较，如图4、图5所示。从两图的比较可以看出当电动机的转速从0阶跃到2 000 r/min时，采用传统的PID控制模式所需的时间是18 ms，转速的最大超量为30%。采用模糊自适应PI控制模式时，阶跃所需时间为14 ms，即所需时间减少22.2%;转速的最大超调量为13%，即为传统PID最大超调量的43.3%。从实验数据可以得出:模糊自适应PI控制是一种优越的控制模式。

［1］李钟明，刘卫国.稀土永磁电动机［M］.北京:国防工业出版社，1999.

［2］李艳，邵日祥，邵世煌.模糊控制在电气传动中的运用现状及前景［J］.电气传动，1997，27（2）:3 －9.

［3］申志强，邹继涛，陈韬，等.张力控制数学模型应用研究［J］.华中科技大学学报:自然科学版，2007，32（12）:65 －67.

［4］席爱民.模糊控制技术［M］.西安:西安电子科技大学出版社，2008.