滚珠丝杠副临界转速研究

汪爱清 战晓明

（南京工艺装备制造有限公司，江苏南京 210004）

高速旋转的滚珠丝杠副相当于一个动力学转子系统，因此对滚珠丝杠副的旋转振动研究可以借鉴转子临界转速的研究方法。与之不同的是在研究丝杠旋转、螺母直线移动工况下的滚珠丝杠副的旋转振动时，可不必考虑由轴上盘状零件旋转引起的“陀螺效应”的影响。除此之外，必须考虑丝杠的轴端安装方式（即约束形式）以及螺母移动过程中作用在丝杠上的附加约束，对丝杠临界转速的影响。

1 滚珠丝杠副旋转系统的动力学分析方法

对于滚珠丝杠副临界转速的研究，首先要建立与滚珠丝杠副等效的转子系统分析模型。进行分析建模时，将滚珠丝杠副系统分成许多不同的单元;从丝杠轴一端的边界条件开始，计算该段的状态参数（挠度、转角、弯矩和剪力），然后根据与其相邻段在此截面处有关参数的约束条件，推算出下一段的状态参数。依次类推，计算到丝杠转轴的另一端。最后根据不同的计算要求及转轴末端的边界条件，完成对滚珠丝杠副系统动力特性的分析［2］。以上分析过程所涉及的转子单元主要包括质量分布均匀的均质轴段单元以及轴段间具有集中质量的弹性支撑单元两种。下面首先给出这两种单元的传递矩阵，然后运用Riccati传递函数矩阵法建立丝杠副等效转子动力学模型，并施加与丝杠实际约束相符的边界条件，最终求得螺母在不同位置时丝杠的临界转速。

1.1 考虑质量的均质轴段的传递矩阵

对于旋转的滚珠丝杠副，其长度与截面直径的比值通常较大，所以在对其进行旋转振动的研究过程中常忽略旋转效应与剪切效应对丝杠临界转速的影响，仅考虑各轴段截面承受的挠度、转角、弯矩和剪力等力学载荷因素的影响。将其受力状态记为状态列阵:Z=［xθM Q］T;对于均质丝杠轴段，其力学状态如图1所示。

由于丝杠轴段单元均布质量的存在，可列出其在X轴方向的力学平衡方程与在X－Z平面内的力矩平衡方程为

式中:M为弯矩，N·m;θ为转角，rad;N为轴向力，N;Q为剪切力，N;J为转动惯量，kg·m2;m为单位长度的质量，kg;x为挠度，m;z为轴段相对丝杠左端面的距离，m。

假设滚珠丝杠副旋转系统做简谐振动:

则将该式代入式（1）中即可得到Euler－Bernoulli（伯努利—欧拉）梁动力学数学模型:

式中:I为轴段惯性矩，m·kg·s2;E为弹性模量，N/m2;ωn为轴段弯曲振动的固有频率，Hz。

对式（2）中所描述的微分方程进行求解可得:

式中:c1、c2、c3、c4是常数，由轴单元的边界条件确定。由此可得:

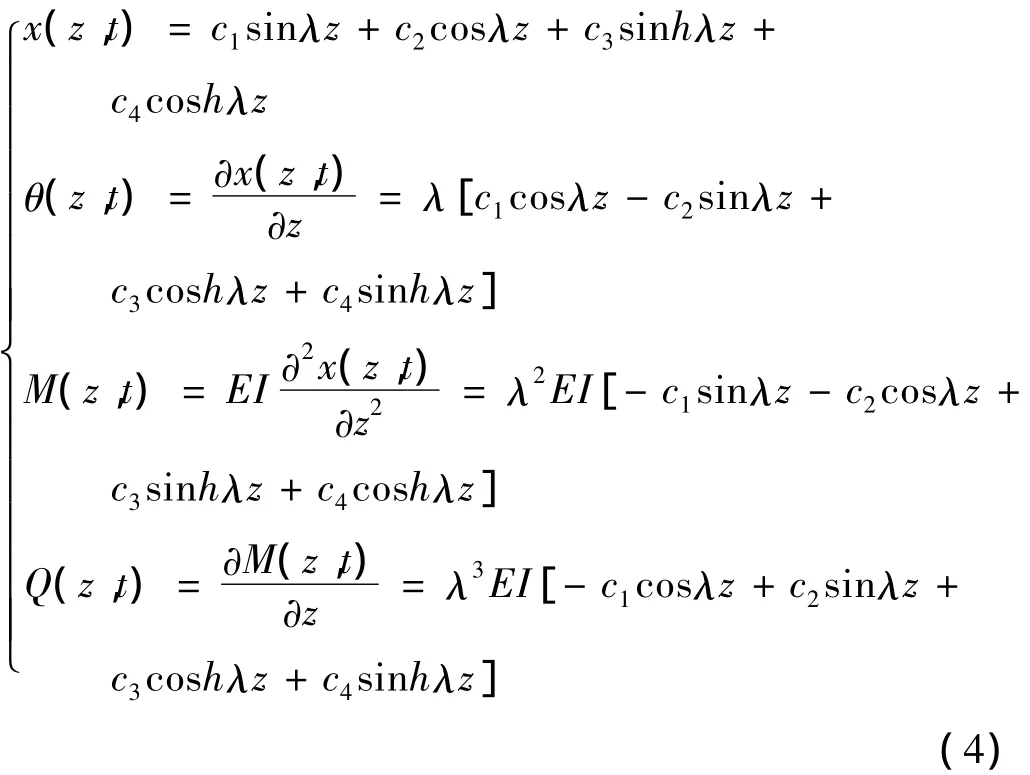
所以位于z=L处的丝杠均质轴段的传递函数矩阵为

式中:P=（coshλL+cosλL）/2，S=（sinhλL+sinλL）/2，R=（coshλL－cosλL）/2，W=（sinhλL－sinλL）/2。

1.2 集中质量与弹性支撑综合作用下的丝杠副综合轴段的传递矩阵

传统意义上的转子系统综合轴段是集集中质量单元、弹性支撑单元以及均质轴单元于一体的综合单元。其传递函数也是由这3种类型的单元集成的综合传递矩阵。滚珠丝杠副旋转系统的综合轴段主要体现在螺母与丝杠的相互作用轴段;在丝杠两端轴颈的轴承连接部位，主要是弹性支撑对其临界转速有影响。

集中质量轴段两截面上的状态参数如图2所示。

其左右两端截面的力学平衡方程为

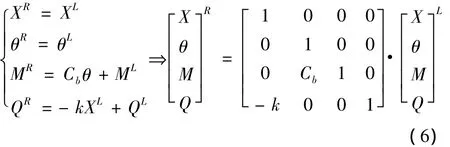
弹性支撑段两截面的状态参数如图3所示。

图3中弹性支撑段弹性支撑具有横向刚度k（N/m）和角向刚度Cb（N·m/rad）两种弹性因素。该种支撑方式将会产生支反力R=kX与支反力矩Mb=Cbθ，则其截面两端的力学平衡方程为:

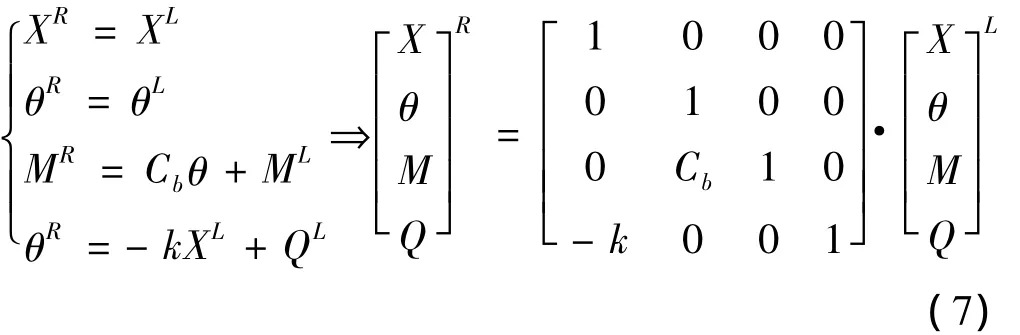
综上两种单元模式，可得出如图4所示的综合轴段的传递矩阵为

式中:l为综合轴段长度，m。

2 Riccati传递矩阵算法

应用Riccati传递矩阵法计算滚珠丝杠副－支撑系统临界转速的基本原理是基于各轴段的传递矩阵与同一截面上的内力与变形参数之间的Riccati传递矩阵进行的，轴系各段的内力与变形参数必须满足已知的边界条件，从而确定轴系的临界转速及相应的振型。其算法实现的主要步骤为［5］:

（1）系统计算模型的建立:将滚珠丝杠副－支撑系统离散成若干轴段，建立相应的综合轴段与均质轴段，准备与各轴段有关的原始数据。

（2）轴段边界条件的判定:实际的边界条件可能有自由端、刚性支撑、弹性支撑、悬臂盘。从计算程序的简化与分析方便的角度出发，一律简化起始、终止边界条件为虚拟自由端，由此可得其边界条件为:

［f］i、［e］i为第i截面上的状态参数列阵Zi的两个子阵，分别对应内力参数列阵［M Q］与变形参数列阵［Xθ］。同一截面上的变形参数与内力参数之间的转换关系即为Riccati变换:

［s］i为第i截面上的Riccati传递矩阵。

根据起始端的边界条件，可以假定起始端截面（截面一）上的 Riccati传递矩阵为:［S］1=0。

（3）依次计算Riccati传递矩阵:在求得由自由端（终止端）截面上的Riccati传递矩阵［S］n+1后，根据边界条件建立频率方程:

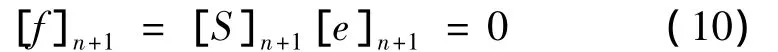
根据右端的边界条件:［e］n+1≠0可得:

该式就是基于Raccti法的频率方程。对于此频率方程的计算可以采用扫频法，即从初始频率开始，按适当的频率步长依次计算，直到频率方程的行列式余值变号，可判断在此频率间隔中应存在一个固有频率。于是采用弦割法或其他有效的迭代逼近方法，求得满足进度要求的临界转速。

3 滚珠丝杠副旋转系统临界转速计算结果与结论

以DKFZD6310R－6－P4/2850×2280滚珠丝杠副为例，进行滚珠丝杠副旋转系统临界转速计算。对于滚珠丝杠副转子动力学系统的边界条件与轴段划分如图5所示。其中包括29个截面、2个自由轴段、23个均质轴段、3个综合轴段，分别计算螺母在丝杠不同位置时的丝杠高速旋转的临界转速，如图6。图中1号线、2号线、3号线、4号线依次标识的是螺母位于距丝杠左端0.461 m、1.031 m、1.373 m、2.513 m等不同位置时丝杠的临界转速变化情况;该图的横坐标反映的是频率方程（11）的求解范围，纵坐标描述的是由频率方程（11）得出的行列式余值Δ的变化，不同编号的曲线在Δ=0时所对应的第一点的横坐标值，即为螺母位于该位置时丝杠的一阶临界转速值。

将图6所示的丝杠一阶临界转速值汇总，见表1。

表1 Riccati矩阵法计算DKFZD6310R－6－P4/2850×2280滚珠丝杠副临界转速值

从表1可以看出丝杠在高速运转过程中，随着螺母位置的变化，丝杠的临界转速经历了一个由小变大、再变小的过程。总体上讲，当螺母位于丝杠滚道最右端有效圈时，丝杠的临界转速最低，大约在2 850 r/min左右;当螺母位于丝杠滚道其他有效位置时，丝杠的临界转速都高于该值，这对该型号滚珠丝杠副的设计选型具有重要的指导意义。

［1］孙红岩，张小龙.基于ANSYS软件的转子系统临界转速及模态分析［J］.机械制造与研究，2008，37（4）:53 －54.

［2］秦然，张建伟.转子临界转速的求解方法比较［J］.沈阳化工学院学报，2007（3）:74－76.

［3］黄金平.转子瞬态动平衡方法研究［D］.西安:西北工业大学，2005（3）.

［4］徐金锁.带细长轴的动力涡轮转子动力特性分析［D］.西安:西北工业大学，2006.

［5］许本文，焦群英.机械振动与模态分析［M］.北京:机械工业出版社.1998.