糯扎渡堆石坝施工期心墙沉降统计模型分析

陈剑龙 王利启

（1.河海大学 水利水电学院，南京 210098；2.水文水资源与水利工程科学国家重点实验室，南京 210098；3.华能澜沧江水电有限公司 糯扎渡电厂筹备处，云南 普洱 665005）

随着西部大开发和西电东送工程的不断推进，高坝大库也越来越多，其中土石坝占多数，有些大坝的坝高在200～300m，坝址地质条件复杂，对工程安全提出了更高的要求.糯扎渡水电站位于云南省思茅市澜沧江下游干流上，是澜沧江中下游河段8个梯级规划的第5级.其主要挡水建筑物心墙堆石坝坝顶高程为821.5m，坝体基本剖面为中央直立心墙形式，心墙两侧为反滤层，反滤层以外为堆石体坝壳.坝顶宽度为18m，心墙基础最低建基面高程为560.0m，高度约为261.5m［1］.

施工期的变形监测是土石坝安全监测重点，沉降是施工期变形监测的重点，应用数学模型进行定量分析是重要的分析工具，因此对施工期心墙的沉降统计模型分析是很有必要的.目前土石坝沉降分析模型主要有：基于土体有效应力的统计模型［2］；基于填筑高度和时间分量的统计模型［3］；采用填筑高度和等效高度作用因子为相关序列，利用灰色GM（1，h）模型建立沉降－填筑间的关系方程［4］；基于遗传蠕变理论的土石坝沉降监测混合模型［5］；统计－支持同量机模型［6］；基于遗传支持向量机的多维灰色变形预测模型［7］；基于人工神经网络的土石坝沉降模型［8］.这些模型有些应用于施工期还需要转换；有些使用起来较复杂；有些因为施工期影响施工计划的因素很多，同时考虑填筑高度与时效的可能会因为与实际发生的施工情况不符而不准确.

本文借鉴传统的施工期沉降统计模型，通过改变使用形式后的结果分析，得到精度高且更为简洁的适合糯扎渡工程的表达.

1 统计模型建立与分析步骤

1.1 回归方程的建立

土石坝防渗区为不透水土料，沉降主要与填土高度，施工含水量和土的特性等因素有关.美国垦务局对20多座土石坝的监测成果表明，其沉降与荷载重量（填土高度）及含水量有关（即有效应力），根据其规律，统计模型可以选用下列表达式［2］：

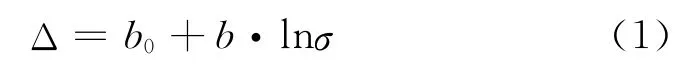
式中，Δ 为压缩率，等于 ΔδV／δV；δV为固结管横梁间的垂直距离；Δδ为压缩量；σ为测点以上直立的土柱重量（γh）扣除测点附近测压计监测的空隙水压力值，也即有效应力.

本文中对式（1）进行一定改变，采取式（2）所示形式对糯扎渡大坝的心墙沉降分析：

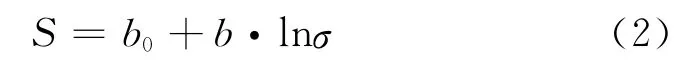
式中，S为测点沉降（mm）；b0，b为回归系数；σ为土体应力（MPa），在下面的分析中σ采用两种形式，其一采用心墙底部的土压力计测得的总土应力及其有效应力；其二采用测点附近的土压力计测得的总土应力及其减去测点附近的渗压计测得的孔隙水压力所得到的有效应力.

1.2 相关系数的显著性检验

在上面的分析中，我们假定沉降S与lnσ之间存在着线性关系.在求得回归方程后，我们必须对这一假定进行检验，以确定沉降S与lnσ的线性相关程度.相关关系用R衡量两个变量x，y呈线性关系的密切程度［9］.

式中，Xt、Yt为相关因子数据为Xt、Yt的平均值.

用子样资料中的lnσ，沉降S代替式（3）中的x，y即可求得相关系数R.然后利用相关系数检验表确定相应显著水平上的相关系数的起码值Rt.当｜R｜≥Rt时，证明回归在相应显著水平上显著，若｜R｜＜Rt，则回归方程不显著.

1.3 方差分析与F检验

沉降监测数据中，同一测点n个不同时间观测值之间存在着差异，我们用观测值y与其平均值的离差平方和来表示这种差异程度记为SYY＝∑（Yt－，不难证明［10］：

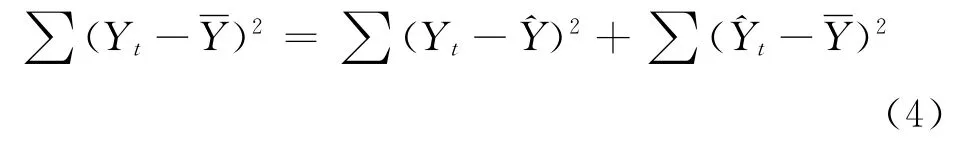
式中，f1，f2分别为回归平方和U和剩余平方和Q的自由度，对于一元线性回归，f1＝1，f2＝n－2，其中n为观测数据量.

求得观测样本F值后通过F分布表查找显著性水平α临界值Fα，若F＜F0.05（1，n－2），则称x与y没有明显的线性关系；若F＜F0.05（1，n－2）＜F0.01（1，n－2），则称x与y有显著的线性关系；若F＞F0.01（1，n－2），则称x 与y 有十分显著的线性关系［10］.相应的也可以用显著性F值（Significance F）来判断，该值是对应显著性水平下的Fα临界值，等于弃真概率P，也即当显著性F值＜0.01时称x与y有十分显著的线性关系.

1.4 残差分析

前面建立了沉降的统计回归模型方程并进行了相关系数检验.在实际的安全监测中，由于观测人员的粗心或偶然因素的干扰，难免出现异常数据.残差分析的目的就在于解决这一问题.所谓残差是指实际观察值与回归估计值的差，即et＝yt－（t＝1，2，…，n）.残差分析就是通过残差所提供的信息，分析出数据的可靠性、周期性或其它干扰.

首先介绍如何借助于数理统计方法检查异常数据.由数理统计理论可以证明残差的方差［10］

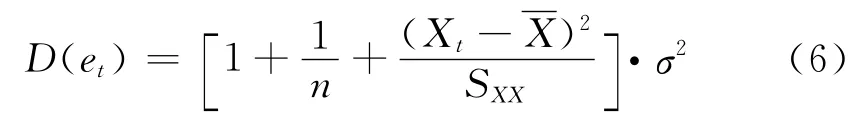
式中，D（e）为残差的方差；σ为回归标准差；n为用于回归的数据量.这说明残差的方差D（e）是x的函数，且二者呈曲线关系.通常较小，常用σ2表示D（et），即D（et）＝σ2，而回归标准差σ一般用剩余标准差估计，从而有D（et）＝σ2＝，根据正态分布的理论，P（－2＝95.44%，也即 P（－）＝95.44%.由此可得置信水平0.045的残差置信带.如果对残差进行标准化处理，则相应的置信区间为（－2，2）.对残差在置信带以外的数据可以认为在所定置信水平下属于异常数据，需要进行检查，以确定是否要剔除掉.剔除后用余下监测数据重新建立回归方程，以提高回归方程的质量.

2 统计模型应用和分析

下面通过心墙最大断面的电磁沉降环数据来应用和分析评价模型.

2.1 数据的预处理

在沉降分析模型式（2）中，土应力因子σ采取了两种形式，因而需对两种形式进行比较分析，而由于沉降、土压力及心墙中渗压计获取的监测数据不完全同期，故需要数据进行处理.本文采用的方法是以因变量沉降S的测读日期为准，将土压力计和渗压计的数据取沉降日期的附近的前后各两个数据共4个数据进行插值.插值通过具体4个数据呈现的规律找到相关系数大于0.99的曲线进行拟合插值.

下面先以心墙最大断面C断面底部的SR01测点沉降数值及其附近的土压力计、渗压计资料的分析介绍模型分析的步骤.

2.2 统计回归分析步骤

首先以总土压力对数lnσ与沉降S进行线性回归分析S＝b1＋b·lnσ.回归曲线如图1所示.

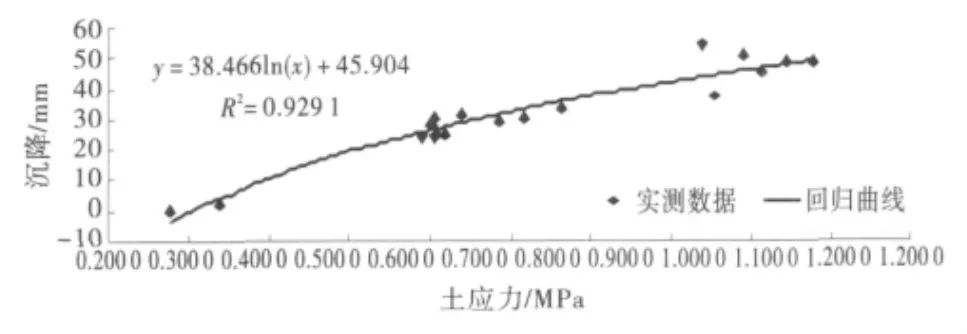
图1 土的总应力回归曲线

通过EXCEL中的数据分析中的回归分析进行处理，在相关系数显著性检验中相关系数R＝0.963 9大于显著水平0.001上的相关系数临界值Rt＝0.693 2，说明回归在0.001水平上显著.同时方差分析中的显著性F值为3.33E－11，说明因变量与自变量之间有很好的回归关系.然而残差分析中15号数据的标准残差为2.77不在置信区间（－2，2）内，而且15号沉降数据为一个跳跃点，不符合沉降的变化规律，应予剔除，用余下的数据重新建立回归方程如图2所示.

图2 剔除异常点后土的总应力回归曲线

重新进行回归分析后，回归效果得到了增强.用剔除异常点后的数据，将式（2）中的σ采用测点附近的土压力计减去测点附近的渗压计的孔隙水压力所得到的有效应力作为自变量时，回归效果如图3所示.

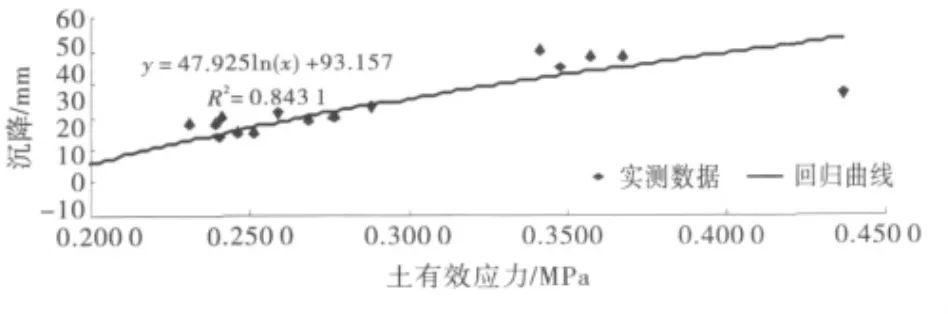
图3 土的有效应力回归曲线

由图2～3对比分析可知，由于孔隙水压力的影响，使得有效应力回归效果不如总土压力.

2.3 模型应用分析

选出心墙最大断面沉降测点中附近既有土压力计又有渗压计的4个测点，每个测点都选用测点附近土压力计及渗压计读数按上述步骤进行回归分析，结果见表1.当各测点都选用心墙最低处也即测点SR01处的土压力计及渗压计的测值进行回归分析时，模型回归分析结果见表2.

表1 心墙沉降不同因子形式模型成果表

表2 心墙沉降回归分析结果表

通过对表1～2的对比分析可知：

1）不管σ采用何种形式，应用总土应力的回归效果好于应用有效应力.

2）综合决定系数和显著性F值比较，σ采用最低处也即SR01处的仪器数据时（所以表1～2中SR01的结果相同）的回归效果好于各测点都采用其附近的仪器数据.

3）当使用测点附近应力回归时，根据残差分析结果，SR18号测点标准残差不在置信区间（－2，2）的数据点较多，而且这些数据的测值多数符合一般的变化规律，并没有明显的异常.该测点的总应力情况下的残差分布如图4所示.

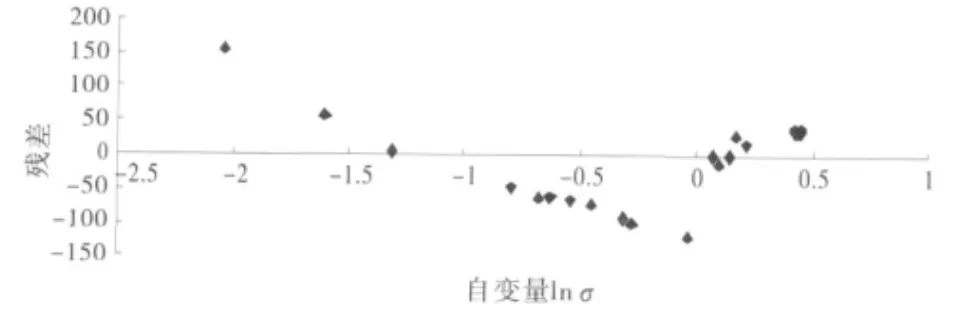
图4 SR18号测点的残差分布图

当残差出现一段全为正（负），接着一段全为负（正），然后又接着一段全为正（负）时，说明回归模型选择不当［10］.应用游程表示残差情况为（＋＋＋）（－－－）（＋＋＋），所以SR18号测点可能是由于模型使用不当使得在置信带外的数据点较多.当使用应力代替应力的对数进行线性回归时，回归结果对比见表3.

表3 SR18号测点模型应用效果比较表

表3表明当改变模型因子形式时，回归效果得到改善.这印证了前面的判断，同时也从另一个方面说明不管采用对数线性还是线性回归，用最低处总土应力的回归效果好于各测点处的总土应力.

3 模型的预测

3.1 模型的选择

通过上述模型应用成果分析可知：

1）孔隙水压力变化较复杂，规律性不强，当将孔隙水应力减去使用有效应力时影响到回归的效果，而且有时影响很大，例如SR41号测点已经达不到线性回归的基本要求.

2）根据有效应力做预测时，既要先预测土应力又要预测孔隙水应力，更加影响到模型的精度.根据回归分析的多个结果，总土应力模型的回归效果一般好于有效应力.

3）如果选用各测点附近的土压力计和渗压计，只有少数几个测点能达到要求，限制了模型的使用范围.而且该种情况下因子不能反映测点下的沉降变化情况.再者根据对比分析，回归效果不如根据最低点总土应力建立的模型.最终以最低处总土压力即包括土应力和孔隙水应力作为模型的因子较合理，通过总土应力反应大坝在施工期填筑过程.模型应用时首先根据第一部分的建模步骤建立土压力与填筑高度的相关模型，利用填筑高度来预测心墙最低点的土应力，然后通过土应力力来预测沉降.这样仅仅使用一个变量填筑高度就能应用该模型来预测沉降，使用起来更加简单.

3.2 模型的预测结果

分别对SR27～SR32号测点与SR40～SR42进行建模预测分析.首先将实测数据分为两个部分，其中2011年7月1日之前的数据建立回归模型，8～9月的数据用于评价预测效果，其中SR27～SR33的建模数据为35个，而SR40～SR42建模数据仅为15个.预测结果见表4.选取其中SR27号测点与SR42号测点作图比较，结果如图5～6所示.

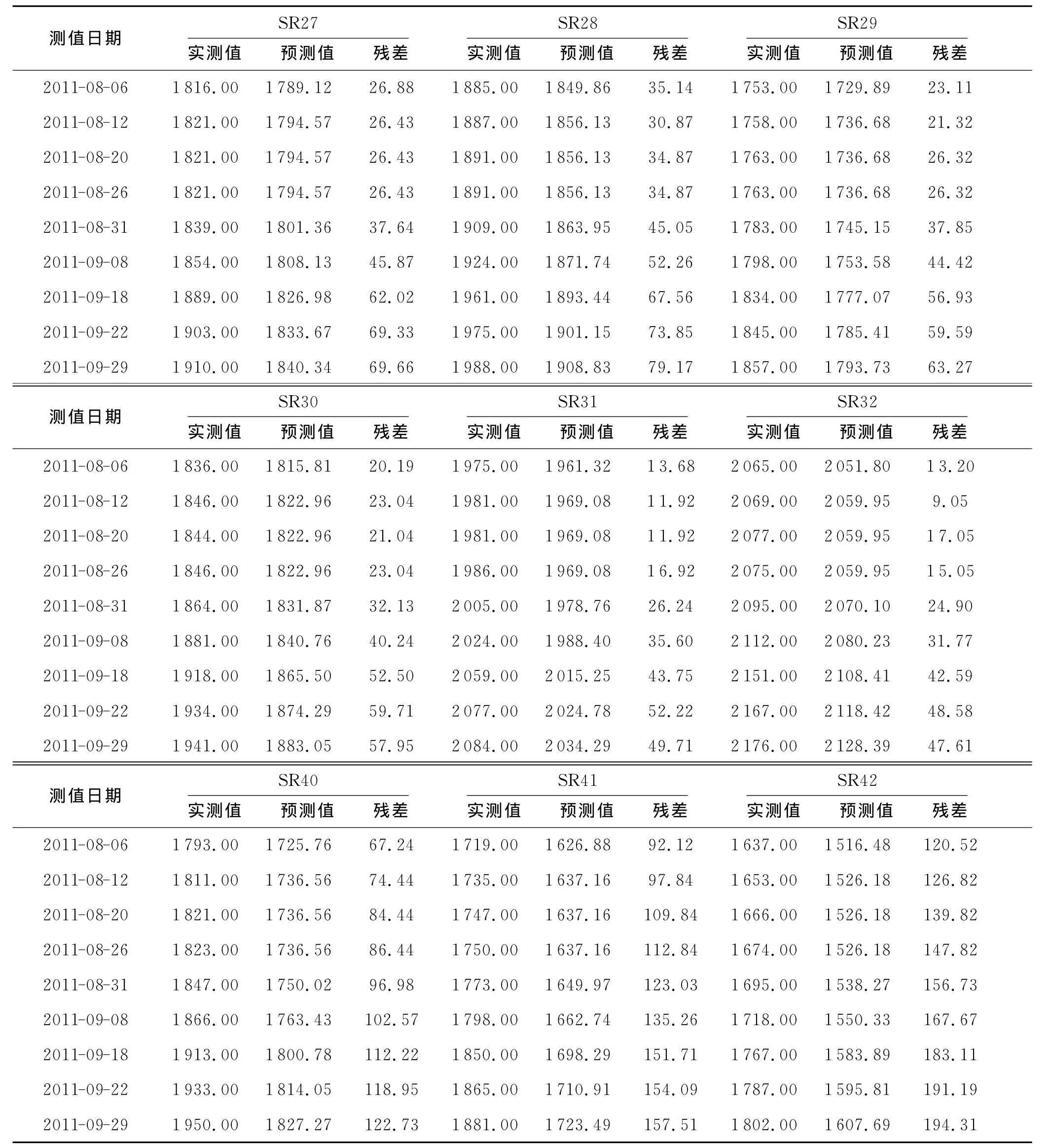
表4 模型预测结果表（单位：mm）

选取SR27号测点利用逐步回归建立统计模型，模型表达式见表5，逐步回归分析所建立的模型表达式中ln（T）为时效因子、H 为填筑高度.其与总土应力回归模型比较见表5与图7.

表5 SR27号测点模型应用比较表

图7 SR27号测点模型预测相对残差比较图

从表4～5及图5～7分析可以得到以下结论：

1）建模数据系列长得到的模型预测效果明显好于建模序列短得到的预测效果.SR27～SR32的预测效果明显好于SR40～SR42.

2）预测后一个月的效果明显好于预测后两个月的数据效果，SR27～SR32号测点的8月份的预测残差占实测值的1%～2%，而且1%占多数，而到9月份的预测残差占实测值的比例2%～4%.

3）从逐步回归与本文所建立的模型比较来看，逐步回归模型决定系数R2稍优于文中所述模型.但从预测效果来看总土应力回归模型更优，而且逐步回归模型形式包含时效因子，具体到施工期影响施工计划的因素众多，故具体应用起来精度会更低.综合比较本文所选取的总土应力回归模型较逐步回归模型精度更高且更为适用于实际工况.

4）总体可以说明只要建立模型序列达到一定数量，预测一定长度的沉降精度较高.

4 结 语

选定心墙最低处的总土应力作为模型的回归因子来反应施工期沉降主要影响因素填筑.通过后面的预测检验可以确定当有一定数量数据建立模型时，预测效果较好，证明该模型在糯扎渡心墙沉降分析中具有适用性，可以作为心墙沉降分析和预测的工具.

［1］ 张宗亮.糯扎渡水电站工程特点及关键技术研究［J］.水力发电，2005，31（5）：4－7.

［2］ 顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用［M］.南京：河海大学出版社，2006.

［3］ 郦能惠，蔡 飞.土石坝原型观测资料分析方法的研究［J］.水电能源科学，2000，18（2）：6－10.

［4］ 黄 铭，刘 俊.土石坝沉降－填筑灰色监测模型分析［J］.上海交通大学学报，2005，39（5）：786－789.

［5］ 黄 铭，黄 伟，刘 俊.基于遗传蠕变理论的土石坝沉降监测混合模型［J］.岩土力学，2004：164－166.

［6］ 赵 卿，黄 超.统计－支持向量机模型在大坝位移分析预测中的应用［J］.测绘信息与工程，2009，34（3）：23－25.

［7］ 罗亦泳，张 豪，张立亭.基于遗传支持向量机的多维灰色变形预测模型研究［J］.浙江工业大学学报，2010：79－83.

［8］ 鞠石泉，顾冲时，侯玉成.基于人工神经网络的土石坝沉降模型［J］.水电能源科学，2005，23（1）：76－78.

［9］ 陈久宇，林 见.观测数据的处理方法［M］.上海：上海交通大学出版社，1987.

［10］何晓群.实用回归分析［M］.北京：高等教育出版社，2008.