基于闭环调整策略的无线HART时间同步方法*

华苗苗，董利达，傅健丰，徐姗姗

(浙江大学信息与电子工程学系，杭州 310027)

无线HART是第一个正式发布的应用于工业过程自动化和控制系统的无线网络通信协议［1］，为无线传感器网络(WSN，Wireless Sensor Networks)在工业领域的应用提供了保障。时间同步对节点的周期睡眠与唤醒、同步测量、数据融合、节点定位等有很重要的作用［2］。WSN的自组织性、多跳性、动态拓扑性和资源受限性，使时间同步方案有其特殊的需求［3］，而工业无线网络复杂多变的环境，对已有时间同步机制更提出了严峻的考验。根据可查阅的资料，无线HART时间同步方面的研究成果较少且描述相对简单［4－5］。目前常用的 WSN 时间同步方法共三类:基于receiver-receiver的同步算法中最典型的是RBS［6］机制，该机制的实现与无线HART提出的基本机制不符，在此不再作描述；基于pair-wise的同步算法中最典型的是TPSN［7］协议；基于sender-receiver的同步算法中最典型的是 DMTS［8］和 FTSP［9］机制。当同步精度要求较高时，TPSN与DMTS都具有通信量大的缺点。基于TPSN进行时钟斜率的估计［10］虽可估计时钟偏差，但是计算较复杂且存储量大，而FTSP机制实现前提是时钟漂移率在短时间内不发生较大变化，因此当它应用于复杂的无线工业环境时，具有一定的局限性。另有研究［11］结合前两种同步算法，以减少同步分组数量，该方法在无线HART的适用性和环境适应性方面还有待改进。

基于无线HART的应用特点，本文提出了基于闭环调整策略的无线 HART时间同步方法——CATS(Closed-loop Adjusting Strategy for Time Synchronization)。该方法通过测量同步节点之间的时间偏差，获得节点之间同步周期时间偏差对象模型参数，建立内部受控对象模型，从而实现节点之间时间偏差的短周期闭环调整，使节点之间的同步精度始终保持在较高的水平。

1 无线HART点对点同步机制

1.1 点对点同步机制介绍

无线HART将时间分成周期性的超帧(Superframe)，将超帧分成若干个时隙(Slot)，每个时隙仅用于一次通信(接收或发送数据)。无线HART基本通信机理［12］如图 1。

图1 时隙通信时序

在无线HART中，节点与时钟源发生的任一通信都可实现时间同步。如节点A要与节点B同步，有两种方法:主动同步和被动同步，如图2所示。一旦节点A发送了需回复ACK的数据给节点B，或接收了来自节点B的数据，都可实现两者的时间同步。主动同步通过ACK中的内容进行同步，被动同步通过DATA到达时间进行同步。

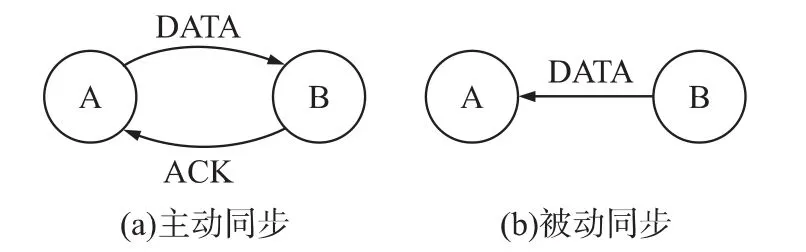
图2 无线HART网络点对点同步方法

1.2 点对点同步精度测试

参照文献［13］测试无线HART点对点同步精度，使用数字示波器观察同步结果。点对点同步误差均值为 1.26 μs，最大值为 6.6 μs，方差为 0.91，同步误差分布如图3所示，可见同步误差符合正态分布。

图3 点对点同步误差分布图

文献［13］的平均同步误差1.10 μs略高于本实验结果，但是其平均同步误差排除了实验过程中少量的非正常同步误差，故本实验得到的同步误差基本达到文献［13］的同步水平，且同步误差分布更集中。

1.3 同步周期内时钟漂移率对时间偏差的影响

时钟漂移率(drift rate)描述了时钟每秒偏移标准时间的微秒数［14］。时钟漂移率不仅因晶振工艺而异，而且还受晶振老化、环境变化以及电源波动的影响。图4为EPSON公司的Tuning Fork晶振单元的频率－温度特性典型图，可见，不同节点的频率在相同温度下会有不同，相同节点的频率随温度变化而变化。

为验证以上结论，从两方面对不同节点的时钟漂移率进行测试。

图4 晶振频率－温度特性图［15］

1.3.1 25℃恒温条件下的时钟漂移率

图5为25℃条件下各节点相对于节点E的时钟漂移率的测试结果。可见，各节点的相对时钟漂移率各不相同。因此，节点间即使在某一瞬间完全达到同步，随后也会马上出现偏差，且不同节点在相同时间内出现的偏差不同。无线HART的最大同步周期为30 s，最大时间偏差为 1 000 μs～1 200 μs［12］，故节点间会因超过最大时间偏差而无法通信。

图5 相对某一节点的时钟漂移图

1.3.2 不同温度条件下的时钟漂移率

测试25℃～50℃的范围内，各节点相对于节点E的时钟漂移率如图6所示。可见，时钟漂移率随温度的升高而减小，且减小幅度不同。因此，不同环境下相同节点间的相对时钟漂移率也各不相同。

图6 不同温度下的时钟漂移率曲线

综上所述，不同节点的时钟漂移率各不相同，相同节点在不同环境下的时钟漂移率也各不相同。为了让节点间的时间偏差始终保持较高的精度，使之适用于复杂的无线环境，可以利用同步周期的同步数据，在时间同步期间对时间偏差进行短周期调整。

2 闭环调整时间同步方法

2.1 点对点时间偏差分析

如节点B为节点A的时钟源，因节点时间由硬件晶振驱动，则时间分别为［16－17］:

其中kA、kB为节点 A、B的晶振的比例系数(Proportional Coefficient)，ωA(t)，ωB(t)为晶振的频率(Frequency)，cA(t0)，cB(t0)为初始时钟偏置，t0为初始时刻，节点A、B在t时刻的时间偏差Δ(t)为:

式中，Δ(t0)=cA(t0)－cB(t0)表示节点A、B间的初始时钟偏差。

由测试结果可知，节点之间的时间偏差会随时间的变化而变化，故通过程序对节点A时间加以调整，设调整值为u(t)，则调整后节点A、B间的时间偏差为

2.2 CATS 方法

CATS方法是一种基于闭环调整策略的点对点时间同步方法，通过在同步期间进行时间偏差调整来提高同步精度。系统采用双周期采样，采样周期分别为:

同步周期:同步节点A与时钟源节点B进行点对点同步的周期，用T表示。

调整周期:同步节点A对本地时间进行调整的周期，用Tc表示。

一个同步周期T包含N次偏差调整，即NTc=T(N∈Z+)。将第k次同步周期内的第n次调整时刻记为(kT，nTc)时刻，其中k=0，1，2，…，n=0，1，2，…，N－1。

CATS方法的实现原理如图7所示。图7中，系统的参考输入ΔrAB(kT，nTc)为

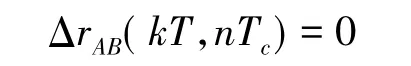
表示控制目标是节点A、B的时间偏差在任何扰动下都能尽快恢复或接近于稳态值0。系统的输出ΔcAB(kT，0Tc)表示(kT，0Tc)时刻节点间的时间偏差；ΔcAB(kT，nTc)表示(kT，nTc)时刻节点间的时间偏差，此时间偏差不可测得。受控对象模型输出Δ(kT，nTc)表示(kT，nTc)时刻节点间的时间偏差估计。系统控制输出uAB(kT，nTc)表示控制调节器在(kT，nTc)时刻对节点间的时间偏差的控制输出，通过节点A调整本地时间实现。对象模型估计器输出Δ(kT)表示节点间在第k次同步周期内的相对时钟漂移率变化量估计值。

图7 CATS系统框图

系统框图分四部分:受控对象、受控对象模型、控制调节器和对象模型估计器。

受控对象:节点A、B间的时间偏差。设开始同步的时刻为初始时刻，即t0=kT，(kT，nTc)时刻为当前时刻，即t=kT+nTc，则将式(4)离散化，得(kT，nTc)时刻的时间偏差:

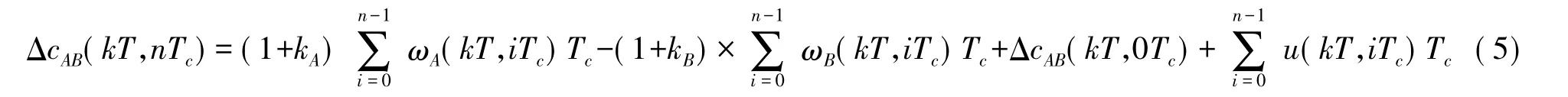
受控对象模型:受控对象的分段线性模型。在同步周期kT内，可合理假设晶振频率保持不变，则A、B节点时钟模型的晶振频率简写为(kT)(kT)。

由于受控对象模型以T为周期分段线性，故在每个同步周期的起始时刻，其估计的时间偏差即为实测的时间偏差，即

表示第k次同步周期内节点A、B之间相对时钟漂移率的估计量。

控制调节器:控制调节器输出使节点间时间偏差接近或等于稳态值0。设计思路为:

(1)点对点同步技术将同步时刻测得的时间偏差完全补偿为0；

(2)同步周期时间内由时钟漂移率产生的时间偏差由控制调节器补偿。

控制输出u(kT，nTc)与u((k－1)T，nTc)的递推关系为:

由式(5)和(6)可得时间偏差估计Δ(kT，nTc)与Δ(kT，(n－1)Tc)递推关系为

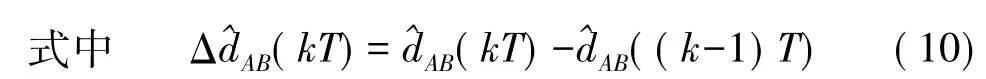
表示第k次同步周期内的相对时钟漂移率变化量的估计值。

对象模型参数估计器:用于估计受控对象模型的参数即相对时钟漂移率的变化值Δ^dAB(kT)。考虑到第k次同步周期的初始时刻(kT，0Tc)时刻即为((k－1)T，NTc)时刻，则

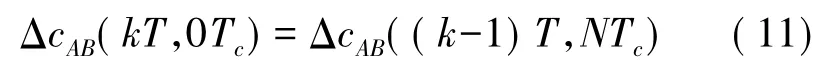
由于相邻同步周期内的相对时钟漂移率变化值差别不大，将ΔdAB((k－1)T)作为第k次同步周期的相对时钟漂移率的估计值，则第k次同步周期内相对时钟漂移率变化量的估计值为

综上所述，CATS使用对象模型参数估计器及时估计相对时钟漂移率变化量，对设备间时间偏差建模并以此为内部受控对象，实现节点间时钟偏差的短周期闭环调整。

3 实验结果及性能分析

3.1 实验平台

实验测试平台包括5个CC2430－f128通信模块、Tektronix TDS 2014B示波器、34 cm×25 cm×10 cm温升盒、WALET 828加温器和ODILLA温度计，如图8所示。

图8 实验平台

3.2 实验结果与对比分析

对FTSP分别做回归表为8和16两种测试［13］，与CATS的测试结果对比。设置超帧长度为100个时隙，同步周期T=30 s，调整周期Tc=50 ms。分别从六方面进行对比。

3.2.1 不同相对漂移率下的同步误差

图9 同步误差随时间变化曲线

添加同步点之间无偏差调整的DMTS作对比，以体现CATS和FTSP方法能使任意节点之间有较低的同步误差。选取相对时钟漂移率为2.75 μs/s、23.88 μs/s 和 47.88 μs/s 的两个节点，分别测得25℃下的同步情况如图9所示。可见，DMTS使节点最大时间同步误差随相对时钟漂移率的增大而增大。当相对时钟漂移率为47.88 μs/s时，由于同步周期内时间偏差超过通信允许最大偏差，从而导致一次同步后就失去同步，如图9(c)所示。统计平均同步误差如表1所示，可见当FTSP的回归表为8时，CATS的同步误差与其相近，当FTSP的回归表为16时，CATS的同步误差小于FTSP。

表1 不同时钟漂移率下同步误差对比

3.2.2 常温下的同步误差

统计CATS和FTSP在常温下的时间同步误差分布。同步误差分布如图10所示，可见CATS的时间误差在－5 μs～7 μs范围内，而 FTSP 的回归表为8 时，范围为－5 μs～ 9 μs，回归表为 16 时，范围为－14 μs～9 μs。

图10 同步误差分布图

CATS与FTSP的同步误差对比如表2所示，可见当FTSP的回归表为8时，CATS的同步误差与其基本一致；回归表为16时，无论是平均同步误差、最大同步误差还是方差，CATS都要优于FTSP。

表2 同步误差对比

3.2.3 不同温度下的平均最大同步误差

在25℃ ～50℃条件下，以节点A为时钟源，测试10 min内节点B、C、D和E的最大同步误差，如图11所示。可见只要温度不变，CATS的平均最大同步误差为6.8 μs，而FTSP方法在回归表为8时，平均最大同步误差为12.75 μs，回归表为16时，平均最大同步误差为 15.25 μs。

图11 不同温度下的平均最大同步误差

3.2.4 不同温度变化率下的平均最大同步误差

在0.1℃/s～0.5℃/s的温度变化率下，以节点A为时钟源，测试5 min内各节点的最大同步误差，如图12所示。从图中可以看出，当温度变化率增大，两种同步方法的平均最大同步误差也增大，但CATS的平均最大同步误差小于FTSP方法，由此可见，相对于FTSP，CATS的环境适应性更强。

图12 不同温度变化率下的最大同步误差

3.2.5 响应时间

将温度以0.5℃/s的温度变化率从25℃提高到50℃，并维持50℃不变，以节点A为时钟源，测试各节点的时间同步回到正常水平需要的时间，如表3所示。由表可见，CATS的响应速度快于FTSP。

表3 响应时间对比

3.2.6 计算复杂性

若调整周期为50 ms，则30 s同步周期内CATS和FTSP的总计算量如表4所示。测试CATS与FTSP的程序运行时间，由于FTSP需根据拟合系数计算理想时间，故程序运行时间是随着应用需记录时间次数的增长而增长，而CATS的本地时间即视为理想时间，故程序运行时间不受应用需记录时间次数的影响。如图13所示，CATS的程序运行时间恒定，而FTSP的程序运行时间随记录时间次数线性增加。

表4 总计算量对比

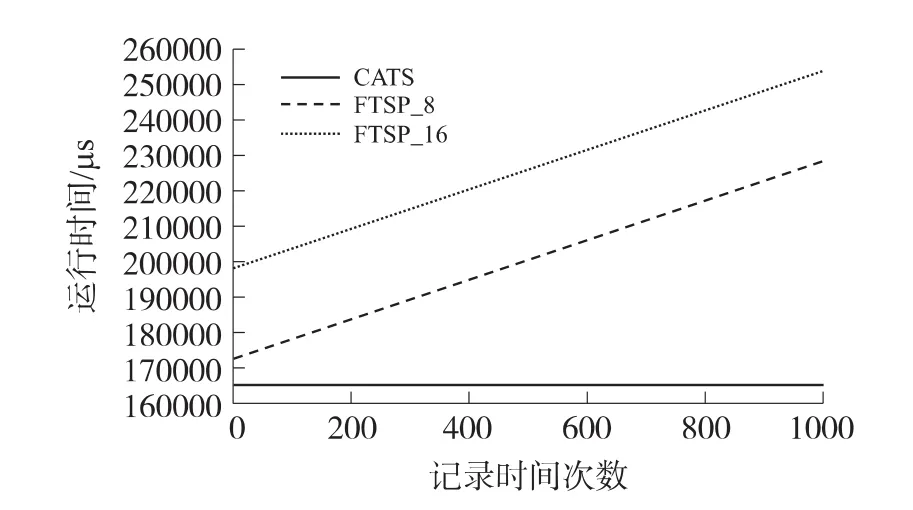
图13 不同记录时间次数下的程序运行时间

4 结束语

本文针对无线HART节点时间同步问题，提出了一种基于闭环调整策略的时钟同步方法。该方法在同步周期内测量同步节点之间的时间偏差，获得同步节点之间时钟偏差对象模型参数，建立内部受控对象模型，在调整周期内实现节点间的时间偏差的闭环调整。实验表明:在通信量相同的情况下，当环境温度变化导致时钟漂移率突变或持续变化时，CATS能降低时间同步误差，此外，此方法还具有同步精度高，计算复杂性低等特点，为复杂工业领域中无线HART时间同步提出了较优方案。

［1］The Hart Communication Foundation.HCF_LIT － 89.Wireless-HART Technical data sheet［S］.USA:2007.

［2］Ferrigno L，Paciello V，Paciello A.Experimental Characterization of Synchronization Protocols for Instrument Wireless Interface［J］.IEEE Transactions on Instrumentation and Measurement，2011，60(3):1037－1046.

［3］周贤伟，韦炜，覃伯平.无线传感器网络的时间同步算法研究［J］.传感技术学报，2006，19(1):20－29.

［4］Kim A N，Hekland F，Petersen S，et al.When HART Goes Wireless:Understanding and Implementing the WirelessHART Standard［C］//13th IEEE International Conference on Emerging Technologies and Factory Automation，Hamburg，Germany，2008:899－907.

［5］赵亦兵，吴志盛，庞涛.基于无线HART网络的时钟同步算法研究［J］.自动化与仪器仪表，2010，4:3－5.

［6］Elson J，Girod L，Estrin D.Fine-Grained Network Time Synchronization using Reference Broadcasts［C］//5th Symposium on Operating Systems Design and Implementation，Boston，Massachusetts，USA，2002:147－163.

［7］Ganeriwal S，Kumar R，Srivastava M B.Timing-Sync Protocol for Sensor Networks［C］//1st International Conference on Embedded Networked Sensor Systems，Los Angeles，California，USA，2003:138－149.

［8］Ping S.Delay Measurement Time Synchronization for Wireless Sensor Networks［D］.Intel Research Berkeley Lab，2003.Http://www.intel_resea－rch.net/publications/Berkele－y/081120－031327_137.pdf，2011－6－30.

［9］Maróti M，Kusy B，Simon G，et al.The Flooding Time Synchronization Protocol［C］//2nd International Conference on Embedded Networked Sensorsystems，Baltimore，USA，2004:39－49.

［10］Chaudhari Q，Serpedin E，Qaraqe K.On Maximum Likelihood Estimation of Clock Offset and Skew in Networks with Exponential Delays［J］.IEEE Transactions on Signal Processing，2008，56(4):1685－1697.

［11］吴成伟，黄文君.无线传感器网络比对广播时间同步算法［J］.传感技术学报，2009，22(12):1789－1794.

［12］The Hart Communication Foundation.HCF_SPEC－075.TDMA Data Link Layer Specification［S］.USA:2008.

［13］Mahmood A，Jantti R.Time Synchronization Accuracy in Real-Time Wireless Sensor Networks［C］//2009 IEEE 9th Malaysia International Conference on Communications，Seri Pacific Hotel，Kuala Lumpur，2009:652－657.

［14］Ctistian F，Fetzer C.The Timed Asynchronous Distributed System Model［J］.IEEE Transactions on Parallel and Distributed System，1999，10(6):181－187.

［15］Epson Toyocom.Frequency Versus Temperature Characteristics［DB/OL］.http://www.epsontoyoc om.co.jp/.english/C_support/glossary/alphaf/index.html，2011－6－30.

［16］Jun Choi B，Xuemin S.Distributed Clock Synchronization in Delay Tolerant Networks［C］//2010 IEEE International Conference on Communications，Cape Town，South Africa，2010:1－6.

［17］Wu Y，Chaudnari Q，Serpedin E.Clock Synchronization of Wireless Sensor Networks［J］.IEEE Signal Processing Magazine，2011，28(1):124－138.